[Swift]LeetCode1039. 多边形三角剖分的最低得分 | Minimum Score Triangulation of Polygon

★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
➤微信公众号：山青咏芝（shanqingyongzhi）
➤博客园地址：山青咏芝（https://www.cnblogs.com/strengthen/）
➤GitHub地址：https://github.com/strengthen/LeetCode
➤原文地址：https://www.cnblogs.com/strengthen/p/10810816.html 
➤如果链接不是山青咏芝的博客园地址，则可能是爬取作者的文章。
➤原文已修改更新！强烈建议点击原文地址阅读！支持作者！支持原创！
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★

热烈欢迎，请直接点击！！！

进入博主App Store主页，下载使用各个作品！！！

注：博主将坚持每月上线一个新app！！！

Given N, consider a convex N-sided polygon with vertices labelled A[0], A[i], ..., A[N-1] in clockwise order.

Suppose you triangulate the polygon into N-2 triangles.  For each triangle, the value of that triangle is the product of the labels of the vertices, and the total score of the triangulation is the sum of these values over all N-2 triangles in the triangulation.

Return the smallest possible total score that you can achieve with some triangulation of the polygon.

Example 1:

Input: [1,2,3]
Output: 6
Explanation: The polygon is already triangulated, and the score of the only triangle is 6.

Example 2:

Input: [3,7,4,5]
Output: 144
Explanation: There are two triangulations, with possible scores: 3*7*5 + 4*5*7 = 245, or 3*4*5 + 3*4*7 = 144.  The minimum score is 144.

Example 3:

Input: [1,3,1,4,1,5]
Output: 13
Explanation: The minimum score triangulation has score 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13.

Note:

1. 3 <= A.length <= 50
2. 1 <= A[i] <= 100

---

给定 N，想象一个凸 N 边多边形，其顶点按顺时针顺序依次标记为 A[0], A[i], ..., A[N-1]。

假设您将多边形剖分为 N-2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 N-2 个三角形的值之和。

返回多边形进行三角剖分后可以得到的最低分。

示例 1：

输入：[1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

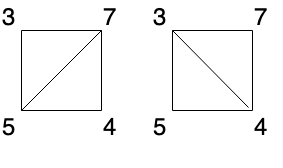
输入：[3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3：

输入：[1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

1. 3 <= A.length <= 50
2. 1 <= A[i] <= 100

---

20ms

class Solution {
    func minScoreTriangulation(_ A: [Int]) -> Int {
        var dp = Array(repeating: Array(repeating: 0, count: A.count), count: A.count + 1)
        for size in 3...A.count {
            for i in 0...A.count - size {
                if size == 3 {
                    dp[size][i] = A[i] * A[i + 1] * A[i + 2]
                } else {
                    var result = Int.max
                    
                    for other in (i + 1)..<(i + size - 1) {
                        var this = A[i] * A[i + size - 1] * A[other]
                        
                        if other > i + 1 {
                            this += dp[other - i + 1][i]
                        }
                        
                        if other < i + size - 2 {
                            this += dp[i + size - other][other]
                        }
                        
                        result = min(result, this)
                    }
                    
                    dp[size][i] = result
                }
            }
        }
        
        return dp[A.count][0]
    }
}

---

Runtime: 36 ms

Memory Usage: 18.8 MB

class Solution {
    func minScoreTriangulation(_ A: [Int]) -> Int {
        var n:Int = A.count
        var dp:[[Int]] = [[Int]](repeating:[Int](repeating:0,count:n),count:n)
        for len in 2..<n
        {
            for i in 0..<(n - len)
            {
                var j:Int = i + len
                dp[i][j] = Int.max
                for k in (i + 1)..<j
                {
                    dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + A[i]*A[j]*A[k])
                }
            }
        }
        return dp[0][n-1]        
    }
}

---

44ms

 

class Solution {
    func minScoreTriangulation(_ A: [Int]) -> Int {
        var memo = [[Int]](repeating: [Int](repeating: 0, count: A.count), count:A.count)
        return dfsHelper(A, 0, A.count - 1, &memo)
    }
    
    fileprivate func dfsHelper(_ A:[Int], _ i:Int, _ j: Int, _ memo: inout [[Int]]) -> Int {
        
        if j < i + 2 {
            return 0 
        }
        if memo[i][j] != 0 {
            return memo[i][j]
        }
        var result = Int.max
        for k in stride(from: i+1, to: j, by: 1) {
            result = min(result, dfsHelper(A, i, k, &memo) + dfsHelper(A, k, j, &memo) + A[i] * A[k] * A[j])
        }
        memo[i][j] = result
        return memo[i][j]
    }
}