[Swift]LeetCode1035.不相交的线 | Uncrossed Lines

★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
➤微信公众号：山青咏芝（shanqingyongzhi）
➤博客园地址：山青咏芝（https://www.cnblogs.com/strengthen/）
➤GitHub地址：https://github.com/strengthen/LeetCode
➤原文地址：https://www.cnblogs.com/strengthen/p/10783476.html 
➤如果链接不是山青咏芝的博客园地址，则可能是爬取作者的文章。
➤原文已修改更新！强烈建议点击原文地址阅读！支持作者！支持原创！
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★

热烈欢迎，请直接点击！！！

进入博主App Store主页，下载使用各个作品！！！

注：博主将坚持每月上线一个新app！！！

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw a straight line connecting two numbers A[i] and B[j] as long as A[i] == B[j], and the line we draw does not intersect any other connecting (non-horizontal) line.

Return the maximum number of connecting lines we can draw in this way.

Example 1:

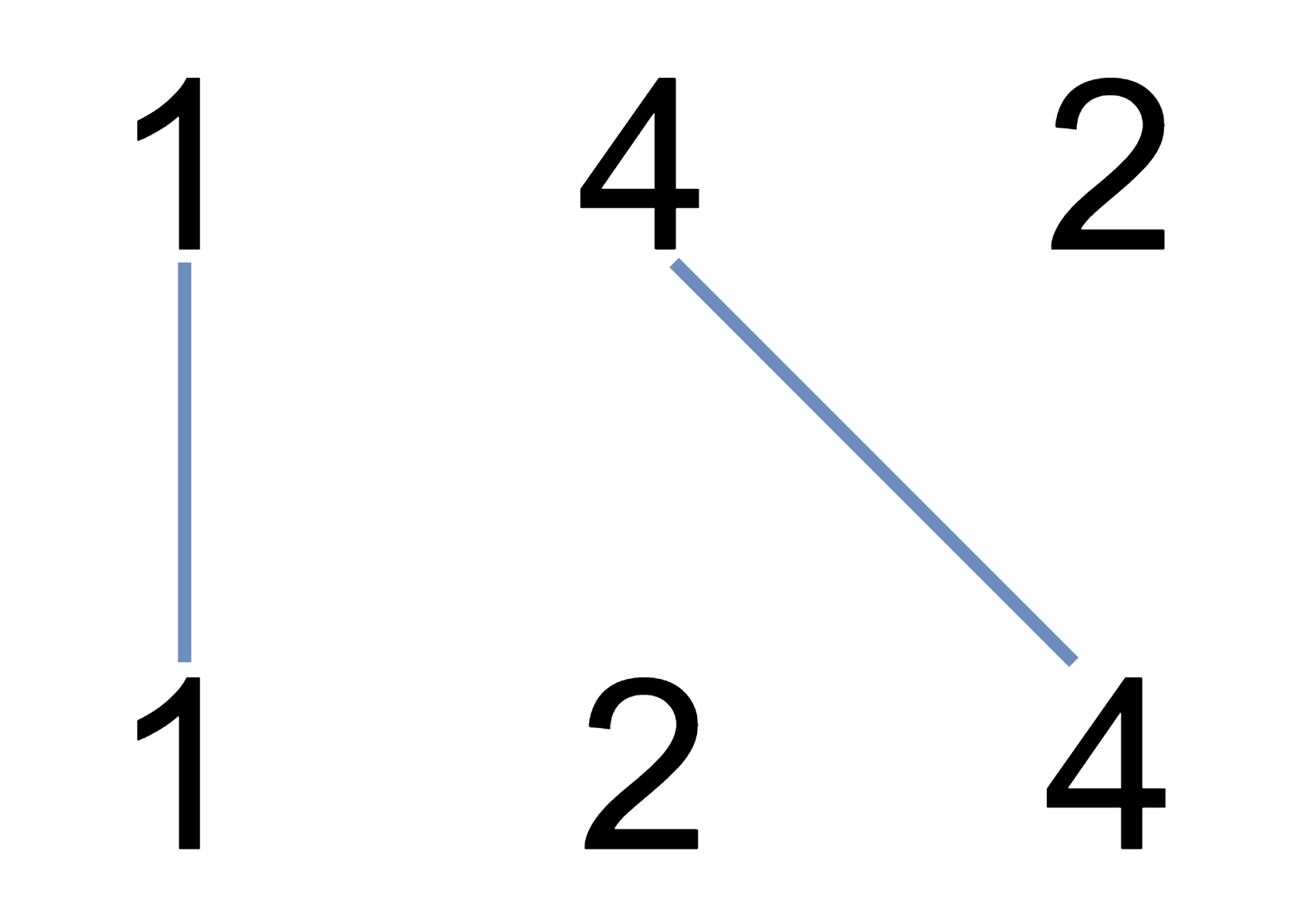
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Example 2:

Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Note:

1. 1 <= A.length <= 500
2. 1 <= B.length <= 500
3. 1 <= A[i], B[i] <= 2000 

---

 我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。

现在，我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且我们绘制的直线不与任何其他连线（非水平线）相交。 

以这种方法绘制线条，并返回我们可以绘制的最大连线数。

示例 1：

输入：A = [1,4,2], B = [1,2,4]
输出：2
解释：
我们可以画出两条不交叉的线，如上图所示。
我们无法画出第三条不相交的直线，因为从 A[1]=4 到 B[2]=4 的直线将与从 A[2]=2 到 B[1]=2 的直线相交。

示例 2：

输入：A = [2,5,1,2,5], B = [10,5,2,1,5,2]
输出：3 

示例 3：

输入：A = [1,3,7,1,7,5], B = [1,9,2,5,1]
输出：2

提示： 

1. 1 <= A.length <= 500
2. 1 <= B.length <= 500
3. 1 <= A[i], B[i] <= 2000

---

76ms

class Solution {
    func maxUncrossedLines(_ A: [Int], _ B: [Int]) -> Int {
        var dp = Array(repeating: Array(repeating: 0, count: B.count), count: A.count)        
        var res = 0        
        for row in 0 ..< A.count {
            for col in 0 ..< B.count {
                dp[row][col] = max(col > 0 ? dp[row][col - 1] : 0, row > 0 ? dp[row - 1][col] : 0)
                if A[row] == B[col] {
                    dp[row][col] = max(dp[row][col], col > 0 && row > 0 ? dp[row - 1][col - 1] + 1 : 1)
                    
                    res = max(res, dp[row][col])
                }    
            }
        }
        return res
        
    }
}

---

Runtime: 84 ms

Memory Usage: 18.7 MB 

class Solution {
    func maxUncrossedLines(_ A: [Int], _ B: [Int]) -> Int {
        let n:Int = A.count
        let m:Int = B.count
        var dp:[[Int]] = [[Int]](repeating:[Int](repeating: 0, count:m + 1),count:n + 1)
        dp[0][0] = 0
        for i in 1...n
        {
            for j in 1...m
            {
                if A[i - 1] == B[j - 1]
                {
                    dp[i][j] = dp[i - 1][j - 1] + 1
                }
                else
                {
                     dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
                }
            }
        }
        return dp[n][m]
    }
}

---

92ms

class Solution {
    func maxUncrossedLines(_ A: [Int], _ B: [Int]) -> Int {                
        var dp = [[Int]](repeating: [Int](repeating: 0, count: B.count+1), count: A.count+1)
        for i in 1...A.count {
            for j in 1...B.count {
                if A[i - 1] == B[j - 1] {
                    dp[i][j] = 1 + dp[i - 1][j - 1]
                } else {
                    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])
                }
            }
        }
        return dp[A.count][B.count]
    }
}

---

196ms

class Solution {
    var dp = [[Int?]]()
    var arrA = [Int]()
    var arrB = [Int]()
    func maxUncrossedLines(_ A: [Int], _ B: [Int]) -> Int {
        arrA = A
        arrB = B
        dp = Array(repeating: Array(repeating: nil, count: B.count), count: A.count)
        
        return helper(startA: 0, startB: 0)
    }
    
    private func helper(startA: Int, startB: Int) -> Int {
        if let result = dp[startA][startB] {
            return result
        }
        
        if startA == arrA.count - 1 && startB == arrB.count - 1 {
            let result = arrA[startA] == arrB[startB] ? 1 : 0
            dp[startA][startB] = result
            return result
        }
        
        if startA == arrA.count - 1 || startB == arrB.count - 1{
            let a = arrA[startA]
            let b = arrB[startB]
            let result: Int
            if a == b {
                result = 1
            } else if startA == arrA.count - 1 {
                result = helper(startA: startA, startB: startB + 1)
            } else {
                result = helper(startA: startA + 1, startB: startB)
            }
            
            dp[startA][startB] = result
            return result
        }
        
        let a = arrA[startA]
        let b = arrB[startB]
        let result: Int
        if a == b {
            result = helper(startA: startA + 1, startB: startB + 1) + 1
        } else {
            result = max(
                helper(startA: startA + 1, startB: startB),
                helper(startA: startA, startB: startB + 1)
            )
        }
        
        dp[startA][startB] = result
        return result
    }
}