[Swift]LeetCode909. 蛇梯棋 | Snakes and Ladders

★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
➤微信公众号：山青咏芝（shanqingyongzhi）
➤博客园地址：山青咏芝（https://www.cnblogs.com/strengthen/）
➤GitHub地址：https://github.com/strengthen/LeetCode
➤原文地址： https://www.cnblogs.com/strengthen/p/10609919.html 
➤如果链接不是山青咏芝的博客园地址，则可能是爬取作者的文章。
➤原文已修改更新！强烈建议点击原文地址阅读！支持作者！支持原创！
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★

热烈欢迎，请直接点击！！！

进入博主App Store主页，下载使用各个作品！！！

注：博主将坚持每月上线一个新app！！！

On an N x N board, the numbers from 1 to N*N are written boustrophedonically starting from the bottom left of the board, and alternating direction each row.  For example, for a 6 x 6 board, the numbers are written as follows:

You start on square 1 of the board (which is always in the last row and first column).  Each move, starting from square x, consists of the following:

• You choose a destination square S with number x+1, x+2, x+3, x+4, x+5, or x+6, provided this number is <= N*N.
  • (This choice simulates the result of a standard 6-sided die roll: ie., there are always at most 6 destinations.)
• If S has a snake or ladder, you move to the destination of that snake or ladder.  Otherwise, you move to S.

A board square on row r and column c has a "snake or ladder" if board[r][c] != -1.  The destination of that snake or ladder is board[r][c].

Note that you only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving.  (For example, if the board is `[[4,-1],[-1,3]]`, and on the first move your destination square is `2`, then you finish your first move at `3`, because you do not continue moving to `4`.)

Return the least number of moves required to reach square N*N.  If it is not possible, return -1.

Example 1:

Input: [
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]
Output: 4
Explanation: 
At the beginning, you start at square 1 [at row 5, column 0].
You decide to move to square 2, and must take the ladder to square 15.
You then decide to move to square 17 (row 3, column 5), and must take the snake to square 13.
You then decide to move to square 14, and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
It can be shown that you need at least 4 moves to reach the N*N-th square, so the answer is 4.

Note:

1. 2 <= board.length = board[0].length <= 20
2. board[i][j] is between 1 and N*N or is equal to -1.
3. The board square with number 1 has no snake or ladder.
4. The board square with number N*N has no snake or ladder.

---

在一块 N x N 的棋盘 board 上，从棋盘的左下角开始，每一行交替方向，按从 1 到 N*N 的数字给方格编号。例如，对于一块 6 x 6 大小的棋盘，可以编号如下：

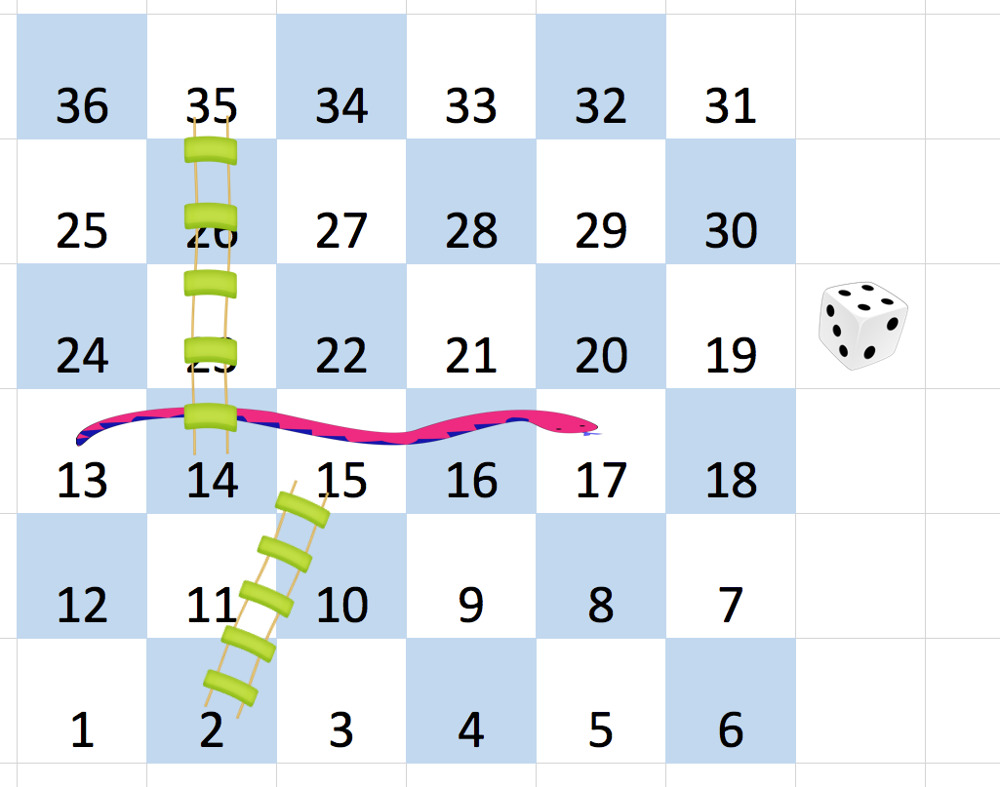
玩家从棋盘上的方格 1 （总是在最后一行、第一列）开始出发。

每一次从方格 x 起始的移动都由以下部分组成：

• 你选择一个目标方块 S，它的编号是 x+1，x+2，x+3，x+4，x+5，或者 x+6，只要这个数字 <= N*N。
• 如果 S 有一个蛇或梯子，你就移动到那个蛇或梯子的目的地。否则，你会移动到 S。 

在 r 行 c 列上的方格里有 “蛇” 或 “梯子”；如果 board[r][c] != -1，那个蛇或梯子的目的地将会是 board[r][c]。

注意，你每次移动最多只能爬过蛇或梯子一次：就算目的地是另一条蛇或梯子的起点，你也不会继续移动。

返回达到方格 N*N 所需的最少移动次数，如果不可能，则返回 -1。 

示例：

输入：[
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]
输出：4
解释：
首先，从方格 1 [第 5 行，第 0 列] 开始。
你决定移动到方格 2，并必须爬过梯子移动到到方格 15。
然后你决定移动到方格 17 [第 3 行，第 5 列]，必须爬过蛇到方格 13。
然后你决定移动到方格 14，且必须通过梯子移动到方格 35。
然后你决定移动到方格 36, 游戏结束。
可以证明你需要至少 4 次移动才能到达第 N*N 个方格，所以答案是 4。 

提示：

1. 2 <= board.length = board[0].length <= 20
2. board[i][j] 介于 1 和 N*N 之间或者等于 -1。
3. 编号为 1 的方格上没有蛇或梯子。
4. 编号为 N*N 的方格上没有蛇或梯子。

---

Runtime: 84 ms

Memory Usage: 19 MB

class Solution {
    func snakesAndLadders(_ board: [[Int]]) -> Int {
        var n:Int = board.count
        var arr:[Int] = [Int](repeating:0,count:n * n)
        var i:Int = n - 1
        var j:Int = 0
        var index:Int = 0
        var inc:Int = 1
        while (index < n * n)
        {
            arr[index] = board[i][j]
            index += 1
            if inc == 1 && j == n - 1
            {
                inc = -1
                i -= 1
            }
            else if inc == -1 && j == 0
            {
                inc = 1
                i -= 1
            }
            else
            {
                j += inc
            }
        }
        var visited:[Bool] = [Bool](repeating:false,count:n * n)
        var q:[Int] = [Int]()
        var start:Int = arr[0] > -1 ? arr[0] - 1 : 0
        q.append(start)
        visited[start] = true
        var step:Int = 0
        while (!q.isEmpty)
        {
            var size:Int = q.count
            while(size > 0)
            {
                var cur:Int = q.removeFirst()
                if cur == n * n - 1
                {
                    return step
                }
                var next:Int = cur + 1
                while(next <= min(cur + 6, n * n - 1))
                {
                    var dest:Int = arr[next] > -1 ? arr[next] - 1 : next
                    if !visited[dest]
                    {
                        visited[dest] = true
                        q.append(dest)
                    }
                    next += 1
                }
                size -= 1
            } 
            step += 1
        }
        return -1
    }
}

---

96ms

class Solution {
    func snakesAndLadders(_ board: [[Int]]) -> Int {
        var flatBoard = [Int]()
        let n = board.count
        var fromLeft = true
        for row in board.reversed() {
            if fromLeft {
                fromLeft = false
                for x in row {
                    flatBoard.append(x)
                }
            } else {
                fromLeft = true
                for x in row.reversed() {
                    flatBoard.append(x)
                }
            }
        }
        flatBoard.insert(0, at: 0)
        var queue = [Int]()
        queue.append(1)
        var counter = [Int](repeating:-1, count: n*n + 1)
        counter[1] = 0
        while queue.count > 0 {
            let curr = queue.removeLast()
            
            for i in 1...6 {
                var next = curr + i
                if next > n*n {
                    break
                }
                if flatBoard[next] != -1 {
                    next = flatBoard[next]
                }
                if next == n*n {
                    return counter[curr] + 1
                }
                if counter[next] == -1 {
                    queue.insert(next, at: 0)
                    counter[next] = counter[curr] + 1
                }
            }
        }        
        return -1
    }
}

---

104ms

class Solution {
    func snakesAndLadders(_ board: [[Int]]) -> Int {
        var newBoard: [Int] = []                
        var movingForward = true
        for i in (0..<board.count).reversed() {
            newBoard += movingForward ? board[i] : Array(board[i].reversed())
            movingForward = !movingForward
        }
        
        var steps = 0
        var queue: [Int] = [0]
        var visited: [Bool] = Array(repeating: false, count: newBoard.count)
        visited[0] = true                
        
        while(!queue.isEmpty) {
            var size = queue.count
            while (size > 0) {
                let curr = queue.removeFirst()            
                if curr >= newBoard.count - 1 {                     
                    return steps
                }        

                let range = curr + 1...min(curr + 6, newBoard.count - 1)              
                for j in range { 
                    let dest = newBoard[j] > -1 ? newBoard[j] - 1 : j
                    if !visited[dest] {  
                        visited[dest] = true
                        queue.append(dest) 
                    }
                }                
                size -= 1
            }
            steps += 1            
        }        
        return -1
    }
}