线性回归

目录

• 提纲
• 基础线性回归模型&损失函数
  • 模型表达
    • 线性模型基本形式
    • 线性模型向量形式
  • 损失函数
• 优化方法（极小化损失函数）
  • 最小二乘 OLS
  • 梯度下降 GD
• 线性回归的推广
  • 多项式回归
  • 广义线性回归
• 正则化

---

参考资料

• 台湾大学 《机器学习基石》视频
• Ng 《机器学习》视频
• 周志华《机器学习》
• 线性回归原理小结
• Lasso回归算法： 坐标轴下降法与最小角回归法小结

---

提纲

1. 基础线性回归模型&损失函数
2. 优化方法（极小化损失函数）
   1. 最小二乘法 OLS
      • 代数法解法
      • 矩阵法解法
   2. 梯度下降 Gradient Descent
3. 线性回归的推广
   1. 多项式回归
   2. 广义线性回归
4. 正则化
   1. L1：Lasso
      • 坐标轴下降法
      • 最小角回归法
   2. L2：Ridge
      • 最小二乘法
      • 梯度下降
   3. L1+L2：弹性网
      • 坐标轴下降法
      • 最小角回归法

基础线性回归模型&损失函数

符号	含义
\(x_j\)	第\(j\)维特征
\(x\)	一条样本中的特征向量，\(x=(1,x_1,x_2,⋯,x_n)\)
\({x^{(i)}}\)	第\(i\)条样本
\(x_j^{(i)}\)	第\(i\)条样本的第\(j\)维特征
\({y^{(i)}}\)	第\(i\)条样本的结果（label）
\(X\)	所有样本的特征全集，即\(X=(x^{(1)},x^{(2)},⋯,x^{(m)})^T\)
\(Y\)	所有样本的label全集，即\(Y=(y^{(1)},y^{(2)},⋯,y^{(m)})^T\)
\(w\)	参数向量，即\(w=(w_0,w_1,⋯,w_n)\)
\(w_j\)	第\(j\)维参数

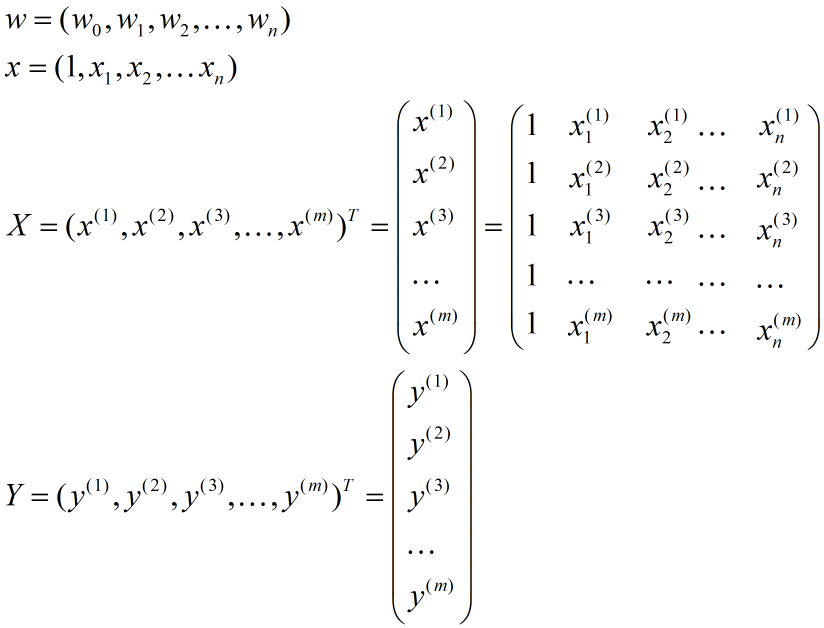
模型表达

线性模型基本形式

\[y(x,w)=w_0+w_1x_1+⋯+w_nx_n \]

其中，\(x_1,x_2,⋯,x_n\)表示自变量（集合）；\(y\)是因变量；\(w\)为参数向量；\(w_i\)表示对应自变量（特征）的权重，\(w_0\)是偏倚项（又称为截距\(b\)）

线性模型向量形式

如果令\(x_0=1\), \(y(x,w)=h_w(x)\), 可以将公式写成向量形式，即

\[h_{w}(x)=\sum_{i=0}^{m}w_{i}x_{i}=w^{T}x \]

其中，\(w=(w_0,w_1,⋯,w_n)\)，\(x=(1,x_1,x_2,⋯,x_n)\) 均为行向量，\(w^T\)为\(w\)的转置。

在一些应用场景中，需要将输入空间映射到特征空间，然后建模. 定义映射函数为\(\phi (x)\)，因此我们可以把公式写成更通用的表达方式：

\[h_{w}(x)=w^{T}\phi (x) \]

损失函数

\[J(w)=\frac{1}{2m}\sum_{i=1}^{m}\left ( h_{w}({x^{i}})-y^{(i)} \right )^2\\ \underset{w}{min}J(w) \]

注意：\(w\)是\(n+1\)维的，而每个\(x\)是\(n\)维的，样本数量为\(m\). 系数1/2只是为后续求导方便计算，而1/m可有可无（但还是前后文统一吧）。

选择使用 误差平方损失极小化 作为优化目标，其实还可以从概率的角度解释（极大似然估计），看下面网址，这里就不写了
http://www.52caml.com/head_first_ml/ml-chapter1-regression-family/

进一步使用矩阵形式表达损失函数

\[J(w)=\frac{1}{2}\left \| Xw^T-Y \right \|^2 = \frac{1}{2}(Xw^T-Y)^2(Xw^2-Y) \]

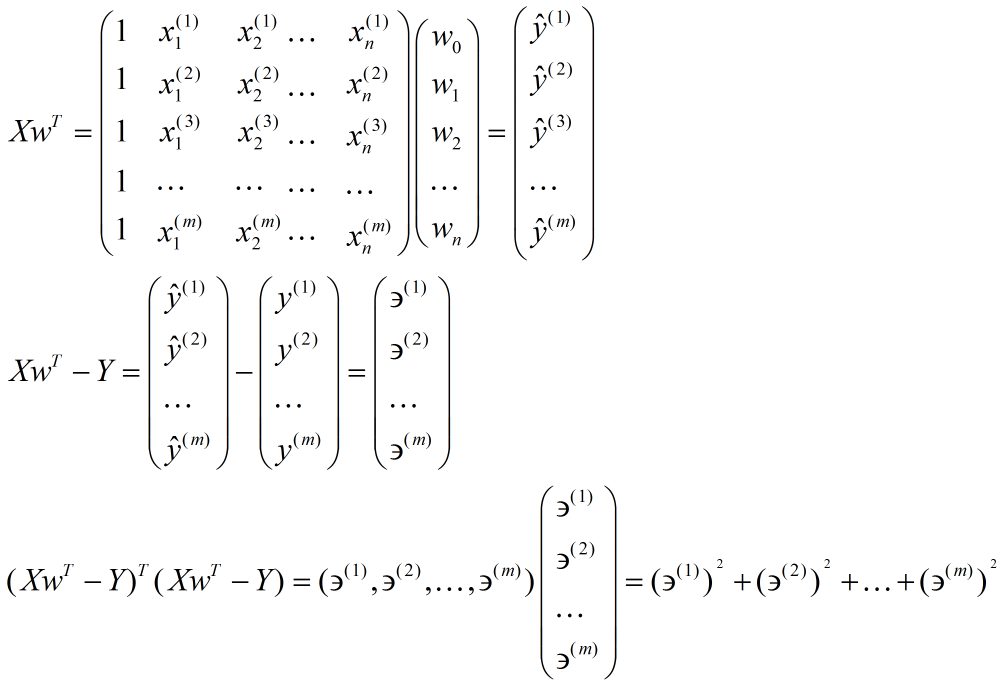
优化方法（极小化损失函数）

最小二乘 OLS

矩阵法（对损失函数进行\(w\) 求导，再令其为0解得\(w\)）：

\[X^TXw=X^TY\\ w=(X^TX)^{-1}X^TY \]

梯度下降 GD

注：梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解

\[J(w)=\frac{1}{2m}\sum_{i=1}^{m}\left ( h_{w}({x^{i}})-y^{(i)} \right )^2 \]

首先，我们对上面的目标函数进行每个参数的单独求导，得到：

\[\frac{\partial }{\partial w_j}J(w)=\frac{1}{m}\sum_{i=1}^{m}\left ( h_{w}({x^{i}})-y^{(i)} \right )\cdot ( x^{(i)}_j ) \]

通过求导结果，可以得到最后的迭代式子：

\[w_j = w_j-\alpha \cdot \frac{1}{m}\sum_{i=1}^{m}\left ( h_{w}({x^{i}})-y^{(i)} \right )\cdot ( x^{(i)}_j ) \]

其中α是步长
注：梯度下降是对每个参数不断的下降，每个参数下降一次需要动用所有样本，所以计算量也蛮大的。有n+1个参数（n+1维），m个样本。

线性回归的推广

多项式回归

回到我们开始的线性模型，\(y(x,w)=w_0+w_1x_1+⋯+w_nx_n\), 如果这里不仅仅是x的一次方，比如增加二次方，那么模型就变成了多项式回归。这里写一个只有两个特征的 p 次方多项式回归的模型：

\[h_θ(x1,x2)=θ_0+θ_1x_1+θ_2x_2+θ_3(x_1)^2+θ_4(x_2)^2+θ_5(x_1x_2) \]

我们令\(x_0=1,x_1=x_1,x_2=x_2,x_3=(x_1)^2,x_4=(x_2)^2,x_5=(x_1x_2)\),这样我们就得到了下式：

\[h_θ(x1,x2)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3+θ_4x_5+θ_5x_5 \]

可以发现，我们又重新回到了线性回归，这是一个五元线性回归，可以用线性回归的方法来完成算法。对于每个二元样本特征\((x_1,x_2)\),我们得到一个五元样本特征\((1,x_1,x_2,(x_1)^2,(x_2)^2,(x_1x_2))\)，通过这个改进的五元样本特征，我们重新把不是线性回归的函数变回线性回归。

广义线性回归

在上一节的线性回归的推广中，我们对样本特征端做了推广，这里我们对于特征 \(y\) 做推广。比如我们的输出\(Y\)不满足和\(X\)的线性关系，但是\(lnY\) 和\(X\)满足线性关系，模型函数如下：

\[lnY=Xw^T \]

这样对与每个样本的输入y，我们用 lny去对应， 从而仍然可以用线性回归的算法去处理这个问题。我们把 Iny一般化，假设这个函数是单调可微函数g(.)g(.),则一般化的广义线性回归形式是：

\[g(Y)=Xw^T 或者 Y=g^{−1}(Xw^T) \]

这个函数\(g(.)\)我们通常称为联系函数。

正则化

线性模型优化目标如下：

\[J(w)=\frac{1}{2m}\sum_{i=1}^{m}\left ( h_{w}({x^{i}})-y^{(i)} \right )^2 \]

但是，当样本特征很多且样本数有限时，按照上面公式求得的参数w容易使得模型陷入过拟合。为了缓解过拟合问题，可引入正则化项。

引入\(L_1\)范数正则化：Lasso

\[J(w)=\frac{1}{2m}\sum_{i=1}^{m}\left ( h_{w}({x^{i}})-y^{(i)} \right )^2+\lambda \left \| w \right \|_1 \]

引入\(L_2\)范数正则化：Ridge

\[J(w)=\frac{1}{2m}\sum_{i=1}^{m}\left ( h_{w}({x^{i}})-y^{(i)} \right )^2+\lambda \left \| w \right \|_2^2 \]

注：
\(\lambda\) 为正则项系数/惩罚项系数
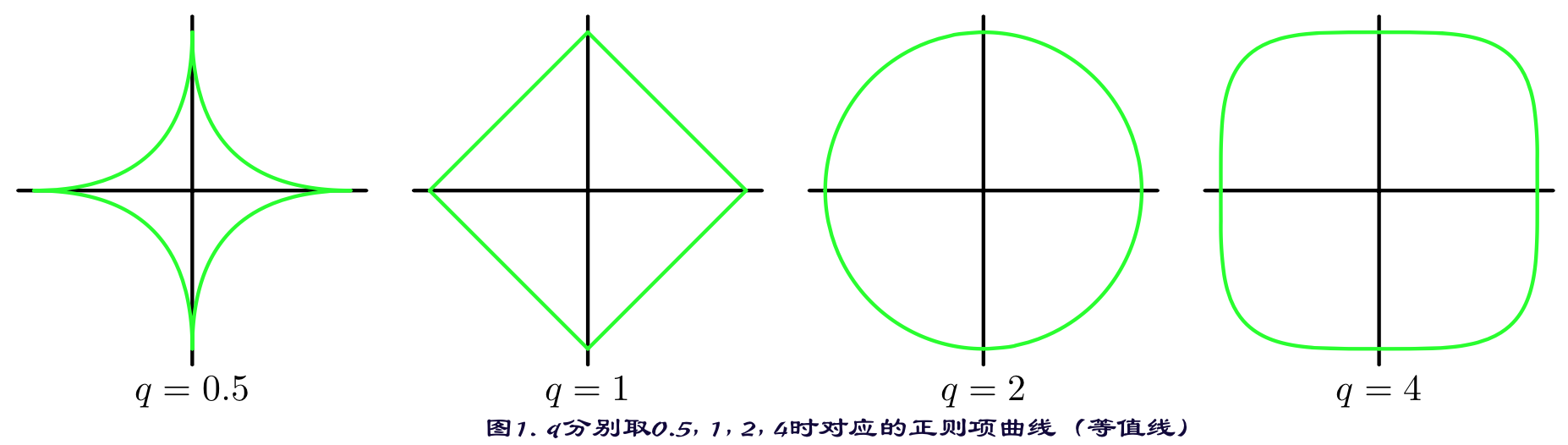
\(L_1\)范数与\(L_2\)范数正则化都有助于降低过拟合风险，但L1还会带来一个额外的好处，就是\(L_1\)正则化更易于获得“稀疏”（sparse）解，即它求得的参数w会有更少的非零分量。 （原因如下图）

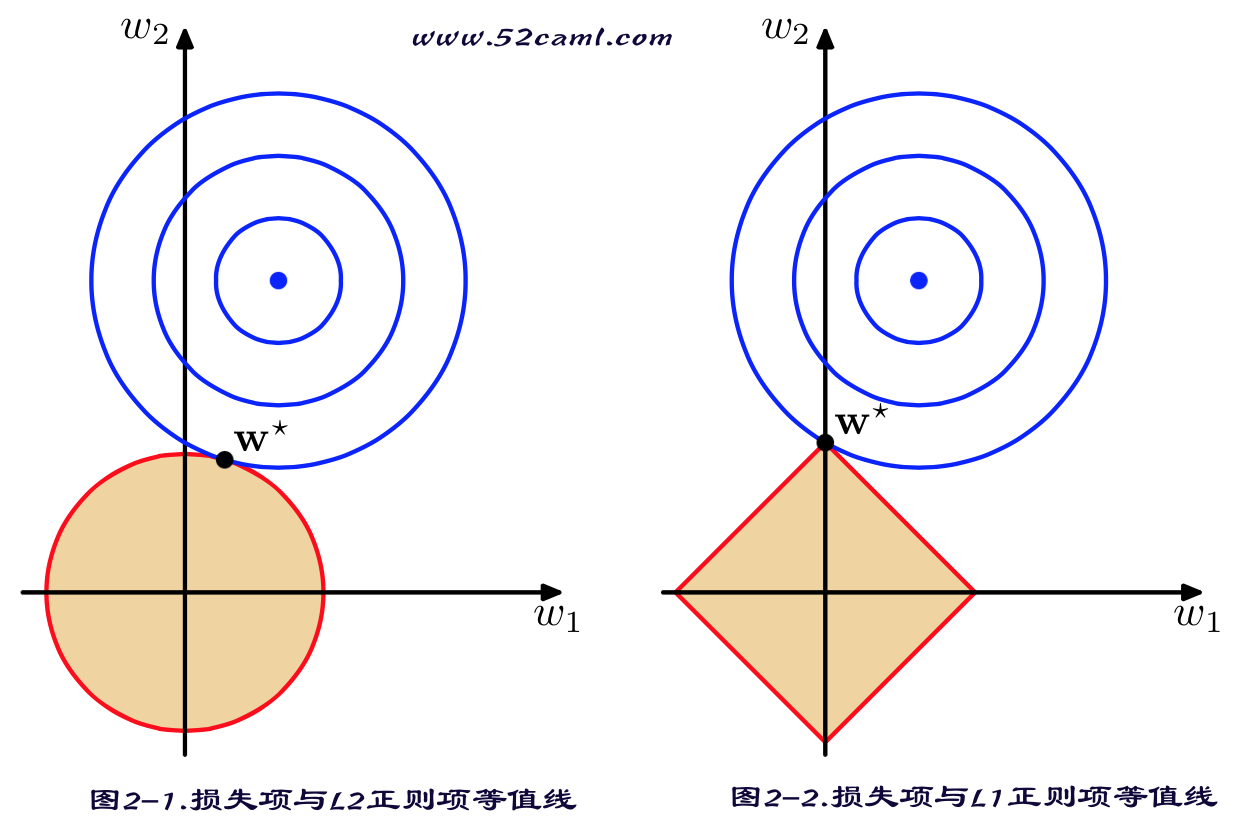
Lasso解法：
因为Lasso所带的\(L_1\)范数正则项不是连续可导的，所以最小二乘与梯度下降这些方法将失效，所以需要使用其他求极值的算法：坐标轴下降法（coordinate descent）和 最小角回归法（ Least Angle Regression， LARS）。

Ridge解法：
同普通线性回归模型一样，加上\(L_2\)范数正则项依旧连续可导，所以继续使用 最小二乘 与 梯度下降。