DirectX透视投影矩阵推导

定义一个相机的位置和方向。知道了相机的位置和方向，我们是通过定义一个平截头体（frustum）来描述相机的范围，裁剪阶段也是依据这个范围空间进行裁剪。平截头体如下：

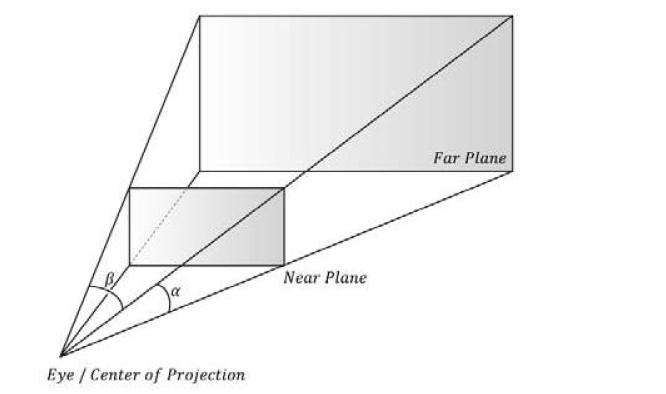
$\alpha$ 表示垂直视角， $\beta$ 表示水平视角，near plane 表示近平面，far plane 表示远平面。

通常，我们在观察空间中使用4个参数定义，以原点为中心，观察方向为 z 轴正方向的 frustum。四个参数分别为：

1. $\mathrm{n}$, 近平面位置
2. $\mathrm{f}$, 远平面位置
3. $\alpha$, 垂直视角
4. $r$, 横纵比 (aspect ratio)

在观察空间中，近平面和远平面都平行于 xy 平面，所以只需要指定他们沿 z 轴方向的距离即可表示这两个平面。横纵比由 $r=w/h$ 表示，其中 w 表示投影窗口的宽度，h 表示投影窗口的高度（单位由观察空间决定）。投影窗口本质是场景在观察空间中的2D图像，而且该图像最终会被映射到后台缓冲区，所以投影窗口的比例应和后台缓冲区的尺寸比例一致。当后台缓冲 区的尺寸为 800×600 时，横纵比 r = 800/600 ≈ 1.333 。不一致会导致变形，比如一个圆被拉伸成椭圆。

---

计算水平视角 $\beta$#

首先，假设一个投影平面，为了方便计算，设高 $h=2$ ，有， $w=2 r$ 。投影面尺寸大小不重要，重要的是比例 $r$ 。同时，设投影面距离视点 为 $d$ 。投影面在哪也无所谓，可以放在近平面，也可以放在 $0-n$ 之间，但是最后发现的是，投影矩阵以及最后得到的坐标都与这个距离 $d$ 无关。

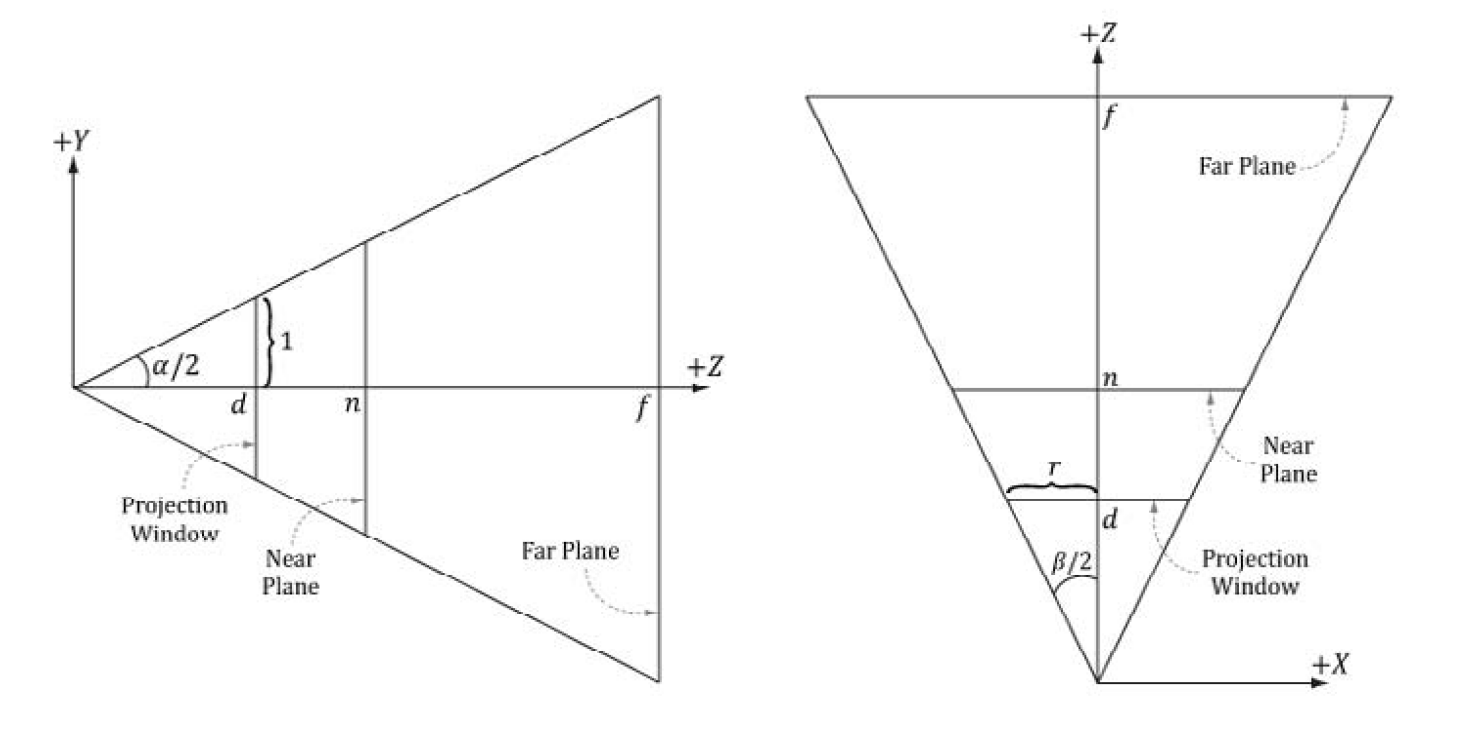
由 $\mathrm{yz}$ 平面，有 $\tan \left(\frac{\alpha}{2}\right)=\frac{1}{d} \rightarrow d=\cot \left(\frac{\alpha}{2}\right)$

由 $\mathrm{xz}$ 平面，有 $\tan \left(\frac{\beta}{2}\right)=\frac{r}{d}=r \cdot \tan \left(\frac{\alpha}{2}\right)$

所以，可以求得水平视角 $\beta$ 。

---

计算投影窗口的投影坐标#

设视觉空间中一个点的坐标为 $(x, y, z)$ ，这个点投影到投影窗口上的坐标为 $\left(x^{\prime} ， y^{\prime} ， d\right)$ ，如图所示。

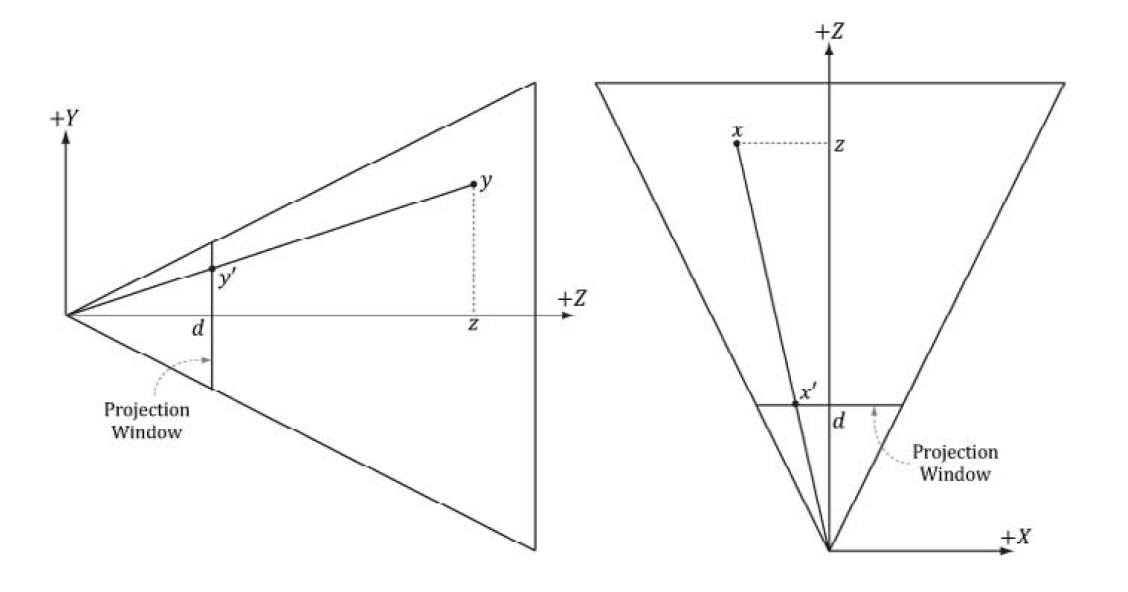
所以，根据三角形相似，有

$$\begin{aligned} &\frac{x^{\prime}}{d}=\frac{x}{z} \rightarrow x^{\prime}=\frac{x d}{z}=\frac{x \cot (\alpha / 2)}{z}=\frac{x}{z \tan (\alpha / 2)} \\ &\frac{y^{\prime}}{d}=\frac{y}{z} \rightarrow y^{\prime}=\frac{y d}{z}=\frac{y \cot (\alpha / 2)}{z}=\frac{y}{z \tan (\alpha / 2)} \end{aligned}$$

因为在 frustum 内的点都会投影到投影面，所以我们可以反推，点 $(x, y, z)$ 在 frustum 中，当且仅当，如下条件被满足时。

1. $-r<x^{\prime}<=r$
2. $-1<y^{\prime}<=1$
3. $n<=z<=f$

规范化设备坐标 (NDC, Normalized Device Coordinates)#

为什么要使用NDC？

1. 设备坐标系（Device），也叫屏幕坐标系，由每一个显示设备（如显示器）的像素点定义，每一个显示设备都有自己单独的坐标系统。还可以进一步在屏幕坐标系统定义一块视图区（view port）
2. 上述计算的投影坐标，依赖投影窗口的横纵比，这也就意味着我们需要为硬件指定横纵比，硬件才可以执行那些与投影窗口尺寸相关的操作（比如，将投影窗口映射到后台缓冲区）
3. 去除横纵比的依赖，可以简化后面的运算。NDC空间的坐标可以通过视口变换映射为设备坐标系下的屏幕坐标。

在NDC空间下，x，y 会规范到 [-1, 1] 之间，z规范到 [0, 1] 之间（d3d中，而在opengl中，z 规范到 [-1, 1]）

所以NDC空间下，点 $(x, y, z)$ 在 frustum 中，当且仅当，

1. $-1<=x^{\prime} / r<=1$
2. $-1<y^{\prime}<=1$
3. $\mathrm{n}<=\mathrm{z}<=\mathrm{f}$

所以，修改上面的投影公式，得到在NDC空间下的投影坐标：

$$\begin{aligned} &x^{\prime}=\frac{x}{r z \tan (\alpha / 2)} \\ &y^{\prime}=\frac{y}{z \tan (\alpha / 2)} \end{aligned}$$

在 NDC 空间中，投影窗口的高度和宽度都为 2。也就是说，现在的尺寸是固定的，硬件不需要知道横纵比，而且我们必须自己来完成投影坐标从观察空间到 NDC 空间的转换工作（图形硬件假定我们会完成这一工作，这个工作也就是视口变换）。

矩阵描述以及透视除法#

现在我们想要把投影变换用矩阵来表示。但是上式中，由于都出现了除以z，而非线性的式子我们无法使用矩阵描述，但是都除以z提醒了我们可以分为两部分处理：先一个线性操作，然后一个除以z的非线性操作，但是我们经过线性变化后，原始的 z 已经丢失，我们需要想办法保存下来原始的深度 z 。解决办法是我们使用齐次坐标的 w 保存 z。所以投影矩阵大致如下：

$$\mathbf{P}=\left[\begin{array}{cccc} \frac{1}{r \tan (\alpha / 2)} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan (\alpha / 2)} & 0 & 0 \\ 0 & 0 & A & 1 \\ 0 & 0 & B & 0 \end{array}\right]$$

矩阵中的 A、B 是两个对 z 线性变换的常量参数，后面会求。

任意一个frustum中的坐标 (x, y, z, 1) 与 投影矩阵乘，可以得到：

$$[x, y, z, 1]\left[\begin{array}{cccc} \frac{1}{r \tan (\alpha / 2)} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan (\alpha / 2)} & 0 & 0 \\ 0 & 0 & A & 1 \\ 0 & 0 & B & 0 \end{array}\right]=\left[\frac{\mathrm{x}}{r \tan (\alpha / 2)}, \frac{\mathrm{x}}{\tan (\alpha / 2)}, A z+B, z\right]$$

然后，每个坐标除以 $w=z$，得到最终结果：

$$\left[\frac{\mathrm{x}}{r \tan (\alpha / 2)}, \frac{\mathrm{x}}{\tan (\alpha / 2)}, A z+B, z\right] \stackrel{}{\longrightarrow}\left[\frac{\mathrm{x}}{r z \tan (\alpha / 2)}, \frac{\mathrm{x}}{z \tan (\alpha / 2)}, A+\frac{B}{z}, 1\right]$$

除以w这一步骤，又被称为透视除法，同时除以w的时候，我们不必担心 w=0，因为 w = z >= n > 0

规范化深度值#

在d3d中，z会被规范到 [0, 1]，令 $g(z)$ 为映射函数，所以有，

$$\begin{aligned} &g(z)=A+\frac{B}{z} \\ &0 \leq g(z) \leq 1 \\ &n \leq z \leq f \end{aligned}$$

将 $z=n$ 和 $z=f$ 带入，有，

$$\begin{aligned} &A+\frac{B}{n}=0 \\ &A+\frac{B}{f}=1 \end{aligned}$$

解得：

$$A=\frac{f}{f-n}, B=-\frac{n f}{f-n}$$

有，

$$g(z)=\frac{f}{f-n}-\frac{n f}{(f-n) z}$$

$g(z)$函数图像：

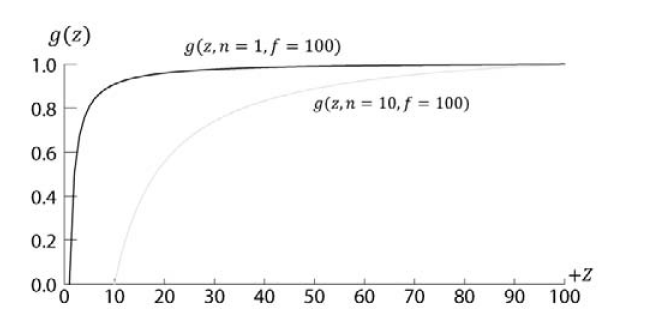
由于图像是非线性的，当 z 接近 近平面 和 远平面 时，都会出现精度问题。通常的建议是让近平面和远平面尽可能接近，把深度的精度性问题减小到最低程度。

最后，投影矩阵：

$$\mathbf{P}=\left[\begin{array}{cccc} \frac{1}{r \tan (\alpha / 2)} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan (\alpha / 2)} & 0 & 0 \\ 0 & 0 & \frac{f}{f-n} & 1 \\ 0 & 0 & \frac{-n f}{f-n} & 0 \end{array}\right]$$

Direct3D 11 中，投影矩阵可通过 XNA 数学库获得。

static XMMATRIX XMMatrixPerspectiveFovLH( // returns projection matrix, LH表示左手坐标系
FLOAT FovAngleY, // vertical field of view angle in radians
FLOAT AspectRatio, // aspect ratio = width / height
FLOAT NearZ, // distance to near plane
FLOAT FarZ); // distance to far plane

相关参考#

Direct3D - 透视投影矩阵与齐次裁剪空间 (goudan-er.github.io)