概述
计算机显示器是一个2D平面。OpenGL渲染时必须将一个3D的场景投影在屏幕上成为一个2D的图片。GL_PROJECTION矩阵的就是用作这种投影变换。首先,其将所有的顶点数据从视觉坐标系(眼坐标系)转化到裁剪空间。然后,通过除以裁剪坐标系中的w分量,将转化后的裁剪坐标变换成标准设备坐标系(NDC)。
因此,我们必须记住GL_PROJECTION集成了裁剪和转化成标准设备坐标系的功能。下面的模块讲述了,如何从以下6个参数建立投影矩阵:left、right、bottom、top、near和far等边界值。
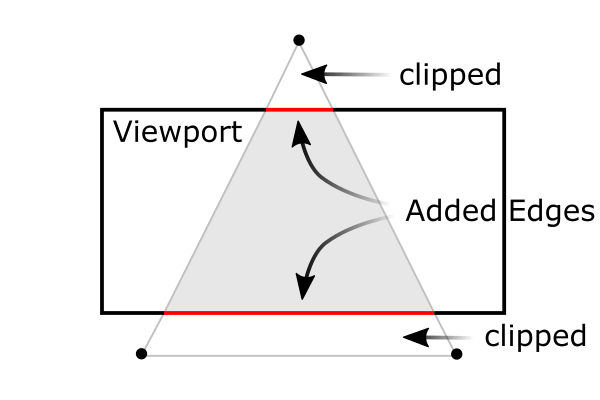
需要注意的是,裁剪空间中的平头截体的裁剪过程发生在,除以\(w_{c}\)分量之前。将裁剪坐标 \(x_{c}\), \(y_{c}\)和\(z_{c}\)和\(w_{c}\)进行比较,如果其中任意一个值小于\(w_{c}\)或者大于\(w_{c}\),那么这个顶点将会被裁剪掉,渲染时会丢弃这个顶点。
\[-w_{c}<x_{c}, y_{c}, z_{c}<w_{c}
\]
当裁剪发生时,OpenGL会重新构建裁剪的边界和边线。
透视投影
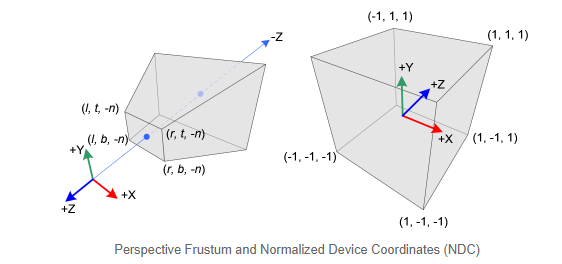
在透视投影时,裁剪截体是一个锥形的,然后被映射到标准设备坐标系中(一个立方体),NDC的x、y和z轴的范围都是从-1至+1。
注意,视觉坐标系是右手坐标系,而NDC使用的是左手坐标系,它们的z值方向是相反的,在视觉坐标系中,摄像机在原点,观察方向为z轴的负值方向,但是在NDC中,摄像机的观察方向却是z轴的正值方向。因此,glFrustum()的near和far参数必须大于0,所以在构建GL_PROJECTION矩阵时,我们必须对它们取反。
在 OpenGL 中,视觉空间中的 3D 点被投影到近平面(投影平面)上。下图显示了视觉空间中的一个点 \(\left(x_{e}, y_{e}\right.\) , \(z_{e}\) ) 是如何在近平面上投影到 \(\left(x_{p}, y_{p}, z_{p}\right)\) 的。
从视雉体的顶视图,眼睛空间的 \(x\) 坐标, \(x_{e}\) 映射到 \(x_{p}\) ,这是通过使用相似三角形的相似计算的;
\[\begin{aligned}
\frac{x_{p}}{x_{e}} &=\frac{-n}{z_{e}} \\
x_{p} &=\frac{-n \cdot x_{e}}{z_{e}}=\frac{n \cdot x_{e}}{-z_{e}}
\end{aligned}
\]
从视锥体的侧视图来看, \(y_{p}\) 也以类似的方式计算;
\[\begin{aligned}
\frac{y_{p}}{y_{e}} &=\frac{-n}{z_{e}} \\
y_{p} &=\frac{-n \cdot y_{e}}{z_{e}}=\frac{n \cdot y_{e}}{-z_{e}}
\end{aligned}
\]
注意 \(x_{p}\) 和 \(y_{p}\) 都依赖于 \(z_{e}\); 它们与 \(-z_{e}\) 呈反比。换句话说,它们都被 \(-z_{e}\) 除以。这是构建GLPROJECTION矩阵的第一个线索。当视觉坐标系的坐标通过乘以GLPROJECTION矩阵转化成裁剪坐标,转化后的裁剪坐标任然是一个齐次坐标。最后通过除以w分量,转化成标准设备坐标系(NDC)。(可以在OpenGL变换中了解更多细节。)
\[\left(\begin{array}{c}
x_{\text {clip }} \\
y_{\text {clip }} \\
z_{\text {clip }} \\
w_{\text {clip }}
\end{array}\right)=M_{p r o j ection } \cdot\left(\begin{array}{c}
x_{\text {eye }} \\
y_{\text {eye }} \\
z_{\text {eye }} \\
w_{\text {eye }}
\end{array}\right),\left(\begin{array}{l}
x_{\text {ndc }} \\
y_{\text {ndc }} \\
z_{\text {ndc }}
\end{array}\right)=\left(\begin{array}{l}
x_{\text {clip }} / w_{\text {clip }} \\
y_{\text {clip }} / w_{\text {clip }} \\
z_{\text {clip }} / w_{\text {clip }}
\end{array}\right)
\]
因此,我们可以将剪辑坐标的 \(w\) 分量设置为 \(-z_{e^{\circ}}\) 并且,矩阵GL_PROJECTION 4 变为 \((0,0,-1,0)\) 。
\[\left(\begin{array}{c}
x_{c} \\
y_{c} \\
z_{c} \\
w_{c}
\end{array}\right)=\left(\begin{array}{cccc}
& \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot \\
0 & 0 & -1 & 0
\end{array}\right)\left(\begin{array}{c}
x_{e} \\
y_{e} \\
z_{e} \\
w_{e}
\end{array}\right), \quad \therefore w_{c}=-z_{e}
\]
接下来,我们将 \(x_{p}\) 和 \(y_{p}\) 映射到具有线性关系的 \(N D C\) 的 \(x_{n}\) 和 \(y_{n }\) 。\([1, r] \Rightarrow[-1,1]\) 和 \([b, t] \Rightarrow[-1,1]\)
然后,我们将 \(x_{p}\) 和 \(y_{p}\) 替换为上述方程。
请注意,我们使每个方程的两个项都可以被 \(-\mathrm{z}_{\mathrm{e}}\) 整除以进行透视除法 \(\left(\mathrm{x}_{\mathrm{C}} / \mathrm{w}_{\mathrm{C}}, \mathrm{y}_{\mathrm{C}} / \mathrm{w}_{\mathrm{C}}\right)\) 。我们之前将 \(\mathrm{w}_{\mathrm{c}}\) 设置为 \(-\mathrm{z}_{\mathrm{e}}\), 括号内的术语将变为剪辑坐标的 \(x_{c}\) 和 \(y_{c}\)
通过这些等式,我们可以得出GL_PROJECTION矩阵的第一行和第二行。
\[\left(\begin{array}{l}
x_{c} \\
y_{c} \\
z_{c} \\
w_{c}
\end{array}\right)=\left(\begin{array}{cccc}
\frac{2 n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\
0 & \frac{2 n}{t-b} & \frac{t+b}{t-b} & 0 \\
& & & \\
0 & 0 & -1 & 0
\end{array}\right)\left(\begin{array}{c}
x_{e} \\
y_{e} \\
z_{e} \\
w_{e}
\end{array}\right)
\]
现在,我们只有第 3 行GL_PROJECTION矩阵要求解。找到 \(z_{n}\) 与其他的有点不同,因为眼睛空间中的 \(z_{e}\) 总是在近平面上投影到\(-n\) 。但是我们需要唯一的 \(z\) 值来进行裁剪和深度测试。另外,我们应该能够取消投影 (逆变换) 它。 由于我们知道 \(z\) 不依赖于 \(x\) 或 \(y\) 值,因此我们借用 \(w\) 分量来查找 \(z_{n}\) 和 \(z_{e}\) 之间的关系。因此,我们可以像这样指定
\[\left(\begin{array}{c}
x_{c} \\
y_{c} \\
z_{c} \\
w_{c}
\end{array}\right)=\left(\begin{array}{cccc}
\frac{2 n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\
0 & \frac{2 n}{t-b} & \frac{t+b}{t-b} & 0 \\
0 & 0 & A & B \\
0 & 0 & -1 & 0
\end{array}\right)\left(\begin{array}{l}
x_{e} \\
y_{e} \\
z_{e} \\
w_{e}
\end{array}\right)
\]
\[z_{n}=z_{c} / w_{c}=\frac{A z_{e}+B w_{e}}{-z_{e}}
\]
在视觉空间中, \(w_{e}\) 等于 1 。因此,等式变为;
\[z_{n}=\frac{A z_{e}+B}{-z_{e}}
\]
为了找到系数 \(A\) 和 \(B\) ,我们使用 \(\left(z_{e}, z_{n}\right)\) 关系; \((-n,-1)\) 和 \((-f, 1)\) ,并将它们放入上面的等式中。
\[\left\{\begin{array} { l }
{ \frac { - A n + B } { n } = - 1 } \\
{ \frac { - A f + B } { f } = 1 }
\end{array} \quad \rightarrow \left\{\begin{array}{l}
-A n+B=-n \\
-A f+B=f
\end{array}\right.\right.
\]
为了求解A和B的方程,重写方程(1)为B
\[B=A n-n
\]
将方程(1')替换为方程(2)中的B,然后求解A;
\[\begin{aligned}
-A f+(A n-n)&=f \\
-(f-n) A&=f+n \\
A&=-\frac{f+n}{f-n}
\end{aligned}
\]
将A放入方程 (1) 中以查找B;
\[\begin{aligned}
\left(\frac{f+n}{f-n}\right) n+B&=-n \\
B &=-n-\left(\frac{f+n}{f-n}\right) n=-\left(1+\frac{f+n}{f-n}\right) n=-\left(\frac{f-n+f+n}{f-n}\right) n \\
&=-\frac{2 f n}{f-n}
\end{aligned}
\]
我们找到了 \(A\) 和 \(B\) 。因此, \(z_{e}\) 和 \(z_{n}\) 之间的关系变为;
\[z_{n}=\frac{-\frac{f+n}{f-n} z_{e}-\frac{2 f n}{f-n}}{-z_{e}}
\]
最后,我们找到了GL_PROJECTION矩阵的所有条目。完整的投影矩阵是
\[\left(\begin{array}{cccc}
\frac{2 n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\
0 & \frac{2 n}{t-b} & \frac{t+b}{t-b} & 0 \\
0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2 f n}{f-n} \\
0 & 0 & -1 & 0
\end{array}\right)
\]
此投影矩阵适用于一般视雉体。如果观看体积是对称的,即 \(r=-l\) 和 \(t=-b\) ,则可以将其简化为;
\[\left\{\begin{array}{l}
r+l=0 \\
r-l=2 r \text { (width) }
\end{array} \quad, \quad\left\{\begin{array}{l}
t+b=0 \\
t-b=2 t \text { (height) }
\end{array}\right.\right.
\]
\[\left(\begin{array}{cccc}
\frac{n}{r} & 0 & 0 & 0 \\
0 & \frac{n}{t} & 0 & 0 \\
0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2 f n}{f-n} \\
0 & 0 & -1 & 0
\end{array}\right)
\]
在我们继续之前,请再次看一下 \(z_{\mathrm{e}}\) 和 \(z_{\mathrm{n}}\) 之间的关系。您注意到它是一个有理函数,并且是 \(z_{\mathrm{e}}\) 和 \(z_{\mathrm{n}}\) 之间 的非线性关系。这意味着在近平面上具有非常高的精度,但在远端平面上的精度非常低。如果范围 \([-n,-f]\) 变大, 则会导致深度精度问题(z-fighting); \(z_{e}\) 在远平面周围的微小变化不会影响 \(z_{n}\) 值。所以n和f的差值尽量小,以尽量减少深度缓冲区精度问题。
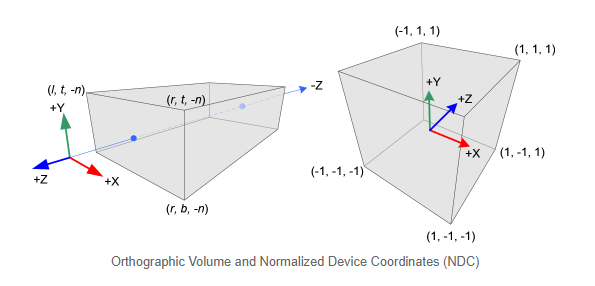
正交投影
眼球空间中所有的 \(x_{e} 、 y e\) 和 \(z_{e}\) 分量都线性映射到 NDC。我们只需要将矩形体积缩放到立方体,然后将其移动到原点。让我们找出使用线性关系GL_PROJECTION的元素。
因为正射投影不需要w分量,所以矩阵的第四行仍然为(0, 0, 0, 1)。因此完整的GL_PROJECTION正射投影矩阵如下:
\[\left(\begin{array}{cccc}
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\
0 & 0 & \frac{-2}{f-n} & -\frac{f+n}{f-n} \\
0 & 0 & 0 & 1
\end{array}\right)
\]
如果观看体积对称,则可以进一步简化它, \(r=-l\) 并且 \(t=-b\) 。
\[\left\{\begin{array}{l}
r+l=0 \\
r-l=2 r \text { (width) }
\end{array} \quad,\left\{\begin{array}{l}
t+b=0 \\
t-b=2 t \text { (height) }
\end{array}\right.\right.
\]
结果
\[\left(\begin{array}{cccc}
\frac{1}{r} & 0 & 0 & 0 \\
0 & \frac{1}{t} & 0 & 0 \\
0 & 0 & \frac{-2}{f-n} & -\frac{f+n}{f-n} \\
0 & 0 & 0 & 1
\end{array}\right)
\]
相关参考
OpenGL Projection Matrix (songho.ca)
3D图形学中的矩阵变换(三) | 王鹏飞 (pengfeixc.com)
观察空间到裁剪空间的投影矩阵推导 · JDreamHeart-知识汇总







 浙公网安备 33010602011771号
浙公网安备 33010602011771号