透视矫正插值 Perspective-Correct Interpolation

> Perspective-Correct Interpolation 翻译仅供学习

(PDF) Perspective-Correct Interpolation (researchgate.net)

透视矫正插值 Perspective-Correct Interpolation

在3D渲染中，输入数据是一些primitive信息，包括顶点位置、颜色、纹理坐标等等。在光栅化阶段，primitive(一般为三角形)被转化成一系列的fragment(或者称为像素)，这些fragment接下来要做ps操作，此时每个fragment都有位置、颜色、纹理坐标这些属性信息，这些属性信息通过顶点属性用插值方法得到的。

就是说在3D图形处理器绘制三角形时，每个像素处的属性信息（包括颜色、纹理坐标等）是对扫描线左右端点对应的顶点属性信息进行插值运算得到的。

1 介绍 INTRODUCTION

我们将推导出（并证明）一种在屏幕空间中通过线性插值实现透视校正插值的方法。在线性图形基元（例如线和多边形）的光栅化过程中，顶点属性的直接屏幕空间线性插值通常不会产生透视正确的结果。

在传统的光栅图形中，颜色、纹理坐标和法向量等属性通常与图形基元的顶点相关联[1,2]。在3D空间中，每个属性的值在每个图形基元之间线性变化。然而，在3D顶点通过透视投影投影到2D图像平面（或屏幕）之后，3D空间中属性值的这种线性变化不会转化为屏幕空间中类似的线性变化。因此，如果我们对屏幕空间中的这些属性值应用直接的线性插值，通常我们会在图像中得到错误的结果。

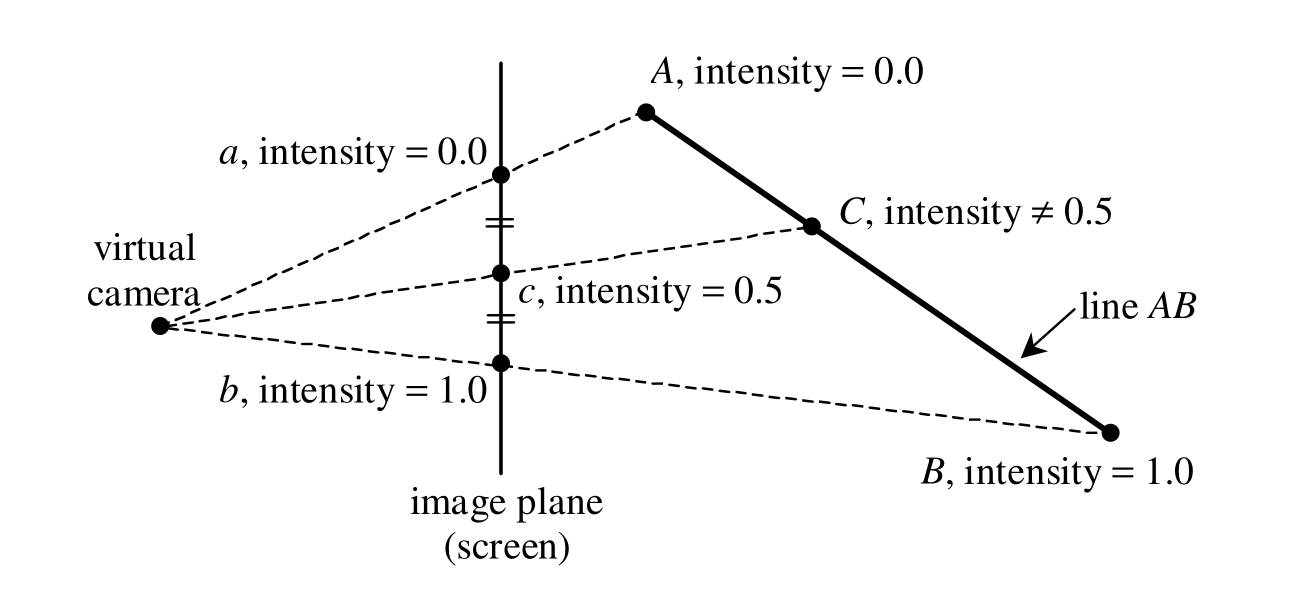
图1：屏幕空间（或图像平面）中属性值的直接线性插值并不总是产生透视正确的结果。

为便于说明，图1仅显示了投影到1D图像平面上的2D空间中的一条线，但可以将相同的参数应用于投影到2D图像平面上的3D线性几何基元。在图中，二维空间中线AB的顶点A和B分别投影到一维图像平面中的点a和b上。顶点处的属性值是强度值（intensity）。在A处，强度值为0.0，在B处，强度值为1.0。因此a和b处的强度值分别为0.0和1.0。假设c是a和b之间的图像平面中点。如果我们在图像平面（或屏幕空间）中对a和b处的强度值进行线性插值，则c处的强度值为0.5。然而，如果我们将点c“反投影”到直线AB上的点C上，我们可以看到C不一定是A和B之间的中点。由于强度值从A到B线性变化（在3D空间中），如果C不是A和B之间的中点，则C处的强度值不应为0.5。

尽管如此，仍然可以通过在屏幕空间中进行线性插值来获得透视正确的结果。这可以通过对属性的某些函数的值进行插值来完成，而不是直接对属性进行插值。然后每个插值结果由另一个函数（反函数）转换，以获得屏幕空间中所需点的最终属性值。您将看到这些函数使用了顶点的z值。

2 插值z INTERPOLATING z-VALUES

在进行透视投影以将图元的3D顶点投影到2D图像平面之前，许多图形渲染系统假设虚拟相机已经位于3D空间的原点，从-z或+z方向看。这定义了一个称为相机坐标系的坐标系。相机的固定观察方向也允许我们始终拥有垂直于z轴的图像平面，这显着简化了透视投影计算。不失一般性，我们将假设相机在+z方向上看，并且图像平面在相机前面的距离为d（见图2）。

许多光栅图形渲染系统使用z-buffer[1,2]来执行隐藏表面去除。这要求在将图元投影到屏幕上的每个像素上，必须知道图元上相应3D点的z坐标（z值）。然而，因为只有图元的顶点被实际投影，它们在屏幕空间中对应的2D图像点是屏幕空间中唯一知道z值的地方。为了更快地光栅化，我们希望使用顶点图像点的已知z值导出其他像素的z值。

z值可以被视为一个属性，其值在3D线性基元中呈线性变化。与我们在图1中看到的示例一样，屏幕空间中z值的直接线性插值并不总是产生透视正确的结果。但是，我们将在下文中看到，我们实际上可以对z值的倒数进行线性插值以获得正确的结果。

与图1类似，图2显示了2D相机坐标系中的一条线被投影到1D图像平面上。标题解释了我们将在公式推导中使用的符号。图中，s为图像平面内的插值参数，t为图元上的插值参数。

图2：虚拟相机在相机坐标系中的+z方向看。图像平面位于相机前方距离d处。A、B和C分别是属性值\(I_{1}, I_{2}\) 和\(I_{t}\)的图元上的点，它们在图像平面上的图像分别为a、b和c。s和t是用于线性插值的参数。

我们的目标是推导出公式以在屏幕空间中正确插入z值。相同的推导可以直接应用于投影到2D图像平面上的3D线性图元（primitive）的情况。

参考图2，由相似三角形，我们有

\[\frac{X_{1}}{Z_{1}}=\frac{u_{1}}{d} \Rightarrow X_{1}=\frac{u_{1} Z_{1}}{d} \tag{1} \]

\[\frac{X_{2}}{Z_{2}}=\frac{u_{2}}{d} \Rightarrow X_{2}=\frac{u_{2} Z_{2}}{d}\tag{2} \]

\[\frac{X_{t}}{Z_{t}}=\frac{u_{s}}{d} \Rightarrow Z_{t}=\frac{d X_{t}}{u_{s}} \tag{3} \]

通过在图像平面（或屏幕空间）中进行线性插值，我们有

\[u_{s}=u_{1}+s\left(u_{2}-u_{1}\right) \tag{4} \]

通过在相机坐标系中对图元进行线性插值，我们有

\[X_{t}=X_{1}+t\left(X_{2}-X_{1}\right) \tag{5} \]

\[Z_{t}=Z_{1}+t\left(Z_{2}-Z_{1}\right) \tag{6} \]

将（4）和（5）代入（3），

\[Z_{t}=\frac{d\left(X_{1}+t\left(X_{2}-X_{1}\right)\right)}{u_{1}+s\left(u_{2}-u_{1}\right)} \tag{7} \]

将（1）和（2）代入（7），

\[\begin{aligned} Z_{t} &=\frac{d\left(\frac{u_{1} Z_{1}}{d}+t\left(\frac{u_{2} Z_{2}}{d}-\frac{u_{1} Z_{1}}{d}\right)\right)}{u_{1}+s\left(u_{2}-u_{1}\right)} \\ &=\frac{u_{1} Z_{1}+t\left(u_{2} Z_{2}-u_{1} Z_{1}\right)}{u_{1}+s\left(u_{2}-u_{1}\right)} \end{aligned} \tag{8} \]

将（6）代入（8），

\[Z_{1}+t\left(Z_{2}-Z_{1}\right)=\frac{u_{1} Z_{1}+t\left(u_{2} Z_{2}-u_{1} Z_{1}\right)}{u_{1}+s\left(u_{2}-u_{1}\right)} \tag{9} \]

可以简化为

\[t=\frac{s Z_{1}}{s Z_{1}+(1-s) Z_{2}} \tag{10} \]

将（10）代入（6），我们有

\[Z_{t}=Z_{1}+\frac{s Z_{1}}{s Z_{1}+(1-s) Z_{2}}\left(Z_{2}-Z_{1}\right) \tag{11} \]

可以简化为

\[Z_{t}=\frac{1}{\frac{1}{Z_{1}}+s\left(\frac{1}{Z_{2}}-\frac{1}{Z_{1}}\right)} \tag{12} \]

等式（12）告诉我们，只需在\(1 / Z_{1}\) 和\(1 / Z_{2}\),之间进行线性插值，然后计算插值结果的倒数，就可以正确导出图像平面中点c处的z值。对于z缓冲区的，甚至不需要计算最终倒数，因为我们只需要在z值比较期间反转比较操作。

3 插值属性 INTERPOLATING ATTRIBUTE VALUES

在这里，我们要推导出公式以在屏幕空间中正确插入其他属性值。再次参考图2。通过在相机坐标系中跨图元线性插值属性值，我们得到

\[I_{t}=I_{1}+t\left(I_{2}-I_{1}\right) \tag{13} \]

将（10）代入（13），我们有

\[I_{t}=I_{1}+\frac{s Z_{1}}{s Z_{1}+(1-s) Z_{2}}\left(I_{2}-I_{1}\right) \tag{14} \]

可以重新排列成

\[I_{t}=\left(\frac{I_{1}}{Z_{1}}+s\left(\frac{I_{2}}{Z_{2}}-\frac{I_{1}}{Z_{1}}\right)\right) /\left(\frac{1}{Z_{1}}+s\left(\frac{1}{Z_{2}}-\frac{1}{Z_{1}}\right)\right) \tag{15} \]

从（12），我们可以看到（15）中的分母只是 \(1 / Z_{i}\)。

所以，

\[I_{t}=\left(\frac{I_{1}}{Z_{1}}+s\left(\frac{I_{2}}{Z_{2}}-\frac{I_{1}}{Z_{1}}\right)\right) / \frac{1}{Z_{t}} \tag{16} \]

式(16)的意思是只要在\(I_{1} / Z_{1}\) 和 \(I_{2} / Z_{2}\)之间进行线性插值，然后将插值结果除以\(1 / Z_{t}\)，就可以正确导出图像平面c点的属性值，它本身可以通过屏幕空间中的线性插值导出，如（12）所示。

参考文献 REFERENCES

[1] James D. Foley, Andries van Dam, Steven K. Feiner and John F. Hughes. Computer Graphics: Principles and Practice, Second Edition. Addison-Wesley, \(1990 .\)

[2] Mason Woo, Jackie Neider, Tom Davis, Dave Shreiner (OpenGL Architecture Review Board). OpenGL Programming Guide, Third Edition: The Official Guide to Learning OpenGL, Version 1.2. Addison-Wesley, \(1999 .\)

Loading

straywriter

透视矫正插值 Perspective-Correct Interpolation