并查集
目录
1558.Segment set
A segment and all segments which are connected with it compose a segment set. The size of a segment set is the number of segments in it. The problem is to find the size of some segment set.

Input
In the first line there is an integer t - the number of test case. For each test case in first line there is an integer n (n<=1000) - the number of commands.
There are two different commands described in different format shown below:
P x1 y1 x2 y2 - paint a segment whose coordinates of the two endpoints are (x1,y1),(x2,y2).
Q k - query the size of the segment set which contains the k-th segment.
k is between 1 and the number of segments in the moment. There is no segment in the plane at first, so the first command is always a P-command.
Output
For each Q-command, output the answer. There is a blank line between test cases.
Sample Input
1
10
P 1.00 1.00 4.00 2.00
P 1.00 -2.00 8.00 4.00
Q 1
P 2.00 3.00 3.00 1.00
Q 1
Q 3
P 1.00 4.00 8.00 2.00
Q 2
P 3.00 3.00 6.00 -2.00
Q 5
Sample Output
1
2
2
2
5
思路:并查集。
从每个集合所唯一的根下手,让根来存储集合内元素个数。
因为无论是合并,还是查找某元素,最终都会追溯到该集合的根。
每次合并的时候,主集合将自己和附属集合的个数和存在主集合内就可以。
不过这要开两个数组来完成啦~一个集合作为father数组,正常的并查集,另一个用来存储集合元素个数。
初始化的时候要使每个元素个数都为1(就是自己)。
#include<iostream>
#include<string>
using namespace std;
const double EPS = 1e-10;
const int MAX=1001;
struct point
{
double x,y;
};
struct line
{
point a,b;
}l[MAX];
int father[MAX],num[MAX];
double Max(double a,double b){return a>b?a:b;}
double Min(double a,double b){return a<b?a:b;}
bool inter(line l1,line l2)
{
point p1,p2,p3,p4;
p1=l1.a;
p2=l1.b;
p3=l2.a;
p4=l2.b;
if( Min(p1.x,p2.x)>Max(p3.x,p4.x) ||
Min(p1.y,p2.y)>Max(p3.y,p4.y) ||
Min(p3.x,p4.x)>Max(p1.x,p2.x) ||
Min(p3.y,p4.y)>Max(p1.y,p2.y) )
return 0;
double k1,k2,k3,k4;
k1 = (p2.x-p1.x)*(p3.y-p1.y) - (p2.y-p1.y)*(p3.x-p1.x);
k2 = (p2.x-p1.x)*(p4.y-p1.y) - (p2.y-p1.y)*(p4.x-p1.x);
k3 = (p4.x-p3.x)*(p1.y-p3.y) - (p4.y-p3.y)*(p1.x-p3.x);
k4 = (p4.x-p3.x)*(p2.y-p3.y) - (p4.y-p3.y)*(p2.x-p3.x);
return (k1*k2<=EPS&&k3*k4<+EPS);
}
void Init(int n)
{
int i;
for(i=1;i<=n;i++)
{
father[i]=i;
num[i]=1;
}
}
int Find(int x)
{
while(father[x]!=x)
x=father[x];
return x;
}
void combine(int a,int b)
{
int temp_a,temp_b;
temp_a=Find(a);
temp_b=Find(b);
if(temp_a!=temp_b)
{
father[temp_a]=temp_b;
num[temp_b]+=num[temp_a];
}
}
int main()
{
int test,i,n,k,js;
char c;
cin>>test;
while(test--)
{
js=0;
cin>>n;
Init(n);
while(n--)
{
cin>>c;
if(c=='P')
{
++js;
cin>>l[js].a.x>>l[js].a.y>>l[js].b.x>>l[js].b.y;
for(i=1;i<js;i++)
{
if(inter(l[js],l[i]))
combine(js,i);
}
}
else
{
cin>>k;
cout<<num[Find(k)]<<endl;
}
}
if(test)
cout<<endl;
}
return 0;
}1811.Rank of Tetris
自从Lele开发了Rating系统,他的Tetris事业更是如虎添翼,不久他遍把这个游戏推向了全球。
为了更好的符合那些爱好者的喜好,Lele又想了一个新点子:他将制作一个全球Tetris高手排行榜,定时更新,名堂要比福布斯富豪榜还响。关于如何排名,这个不用说都知道是根据Rating从高到低来排,如果两个人具有相同的Rating,那就按这几个人的RP从高到低来排。
终于,Lele要开始行动了,对N个人进行排名。为了方便起见,每个人都已经被编号,分别从0到N-1,并且编号越大,RP就越高。
同时Lele从狗仔队里取得一些(M个)关于Rating的信息。这些信息可能有三种情况,分别是"A > B","A = B","A < B",分别表示A的Rating高于B,等于B,小于B。
现在Lele并不是让你来帮他制作这个高手榜,他只是想知道,根据这些信息是否能够确定出这个高手榜,是的话就输出"OK"。否则就请你判断出错的原因,到底是因为信息不完全(输出"UNCERTAIN"),还是因为这些信息中包含冲突(输出"CONFLICT")。
注意,如果信息中同时包含冲突且信息不完全,就输出"CONFLICT"。
Input
本题目包含多组测试,请处理到文件结束。
每组测试第一行包含两个整数N,M(0<=N<=10000,0<=M<=20000),分别表示要排名的人数以及得到的关系数。
接下来有M行,分别表示这些关系
Output
对于每组测试,在一行里按题目要求输出
Sample Input
3 3
0 > 1
1 < 2
0 > 2
4 4
1 = 2
1 > 3
2 > 0
0 > 1
3 3
1 > 0
1 > 2
2 < 1
Sample Output
OK CONFLICT UNCERTAIN
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <queue>
#define MAX_NUM 100010
using namespace std;
//该结构体用来存储 比某个值小的节点,模仿临界表后边的链表
typedef struct Node
{
int num;//数值
Node *next;
}Node;
//用来模仿临界表的数组
struct
{
int rd;//入度
Node *next;
}vect[MAX_NUM];
// N、M 分别表示要排名的人数以及得到的关系数
int N,M;
int sum;//用来记录总元素个数
int A[MAX_NUM],B[MAX_NUM];
char oper[MAX_NUM];//比较运算符
//根,用来判断是否为一个序列
int root[MAX_NUM];
//拓扑排序中使用,用来模仿临界表,这里的next用来记录比他大的所有的元素
int que[MAX_NUM],front,rear;//模拟队列
//找到根
int find_root(int a)
{
if(root[a] == a)return a;
return root[a] = find_root(root[a]);
}
//合并两个集合
int union_set(int a,int b)
{
a = find_root(a);
b = find_root(b);
if(a==b)return 0;
root[b]=a;
return 1;
}
//初始化
void init()
{
memset(vect,0,sizeof(vect));
for(int i=0;i<N;i++)
root[i]=i;
rear = front = 0;
}
void addNode(int a,int b)
{
Node *no = (Node*)malloc(sizeof(Node));
no->num=b;
no->next = vect[a].next;
vect[a].next = no;
vect[b].rd++;
}
//交换两个元素
void swap(int &a,int &b)
{
int tem = a;
a = b;
b = tem;
}
//拓扑排序
void top_order()
{
bool uncertain=false;
//将入度为0,且是根的节点放入队列中,
//若队列中的结点个数大于,则说明信息不全
for(int i = 0;i < N;i++)
{
if(vect[i].rd==0&&find_root(i)==i)
que[rear++] = i;//入队,同时尾指针加1
}
while(front!=rear)
{
if(rear-front>1)//出现信息不全的情况
uncertain = true;
int cur = que[front++];
sum--;
for(Node *i=vect[cur].next;i!=NULL;i=i->next )
{
if(--vect[i->num].rd==0)
que[rear++]=i->num;
}
}
if(sum>0)printf("CONFLICT\n");
else if(uncertain)printf("UNCERTAIN\n");
else printf("OK\n");
}
int main()
{
int a,b;
while(scanf("%d%d",&N,&M)!=EOF)
{
init();
sum = N;
for(int i=0;i<M;i++)
{
scanf("%d %c %d",&A[i],&oper[i],&B[i]);
if(oper[i]=='=')
{
if(union_set(A[i],B[i]))//合并两个元素的集合合并,总数减少1
sum--;
}
}
for(int i=0;i<M;i++)
{
if(oper[i]=='=')continue;
a = find_root(A[i]);
b = find_root(B[i]);
if(oper[i]=='<')
swap(a,b);
addNode(a,b);
}
top_order();
}
return 0;
}1829.A Bug's Life
Background
Professor Hopper is researching the sexual behavior of a rare species of bugs. He assumes that they feature two different genders and that they only interact with bugs of the opposite gender. In his experiment, individual bugs and their interactions were easy to identify, because numbers were printed on their backs.
Problem
Given a list of bug interactions, decide whether the experiment supports his assumption of two genders with no homosexual bugs or if it contains some bug interactions that falsify it.
Input
The first line of the input contains the number of scenarios. Each scenario starts with one line giving the number of bugs (at least one, and up to 2000) and the number of interactions (up to 1000000) separated by a single space. In the following lines, each interaction is given in the form of two distinct bug numbers separated by a single space. Bugs are numbered consecutively starting from one.
Output
The output for every scenario is a line containing "Scenario #i:", where i is the number of the scenario starting at 1, followed by one line saying either "No suspicious bugs found!" if the experiment is consistent with his assumption about the bugs' sexual behavior, or "Suspicious bugs found!" if Professor Hopper's assumption is definitely wrong.
Sample Input
2
3 3
1 2
2 3
1 3
4 2
1 2
3 4
Sample Output
Scenario #1: Suspicious bugs found!
Scenario #2: No suspicious bugs found!
#include <iostream>
#include <stdio.h>
using namespace std;
int _case, bug, flag, action, a, b;
int father[2100], r[2100];
//r表示和父节点的关系,0表示同性
int root(int x)
{
int temp;
if(x == father[x])
return father[x];
//路径压缩
temp = root(father[x]);
r[x] = (r[x]+r[father[x]]) % 2;//路径压缩时,修改节点和祖先的关系
father[x] = temp;
return father[x];
}
void Union(int x,int y)
{
int fx = root(x);
int fy = root(y);
if(fx != fy)
{
/*if(father[x] == fx )
cout<<"hhhhhhhh"<<endl;
else
cout<<"aaaaaaaaa"<<endl;*/
father[fx] = fy;
//归并后修改关系
if(r[y] == 0)
r[fx] = 1 - r[x];
else
r[fx] = r[x];
}
else //已经有相同祖先
{
if(r[x] == r[y])
flag = 1;//他们是同性
}
}
int main()
{
scanf("%d",&_case);
for(int t=1;t<=_case;t++)
{
flag = 0;
printf("Scenario #%d:\n",t);
scanf("%d%d",&bug,&action);
for(int i=1;i<=bug;i++)
{
father[i] = i;
r[i] = 0;
}
while(action--)
{
scanf("%d%d",&a,&b);//虫子编号
if(flag == 0)
Union(a,b);
}
if(flag == 1)
printf("Suspicious bugs found!\n");
else
printf("No suspicious bugs found!\n");
printf("\n");
}
return 0;
}
1198.Farm Irrigation
Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.
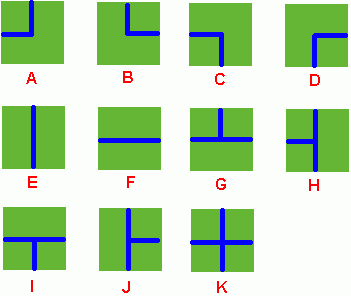
Figure 1
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map
ADC
FJK
IHE
then the water pipes are distributed like
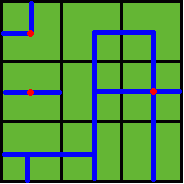
Figure 2
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.
Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?
Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.
Input
There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.
Output
For each test case, output in one line the least number of wellsprings needed.
Sample Input
2 2
DK
HF
3 3
ADC
FJK
IHE
-1 -1
Sample Output
2 3
#include<stdio.h>
#include<string.h>
int a[500][500];
int m,n;
void dfs(int x,int y)
{
int next[5][3]={{0,1},{1,0},{0,-1},{-1,0}};//方向数组
int i,j,tx,ty;
if(x<0||x>m*3||y<0||y>n*3)//越界判断
return ;
if(a[x][y]==1)
{
a[x][y]=0;//能够连通的点全部删除
for(i=0;i<=3;i++)
{
dfs(x+next[i][0],y+next[i][1]);
}
}
}
int main()
{
int t[50][3]={{0,1,0},{1,1,0},{0,0,0},{0,1,0},{0,1,1},{0,0,0},{0,0,0},{1,1,0},{0,1,0},
{0,0,0},{0,1,1},{0,1,0},{0,1,0},{0,1,0},{0,1,0},{0,0,0},{1,1,1},{0,0,0},
{0,1,0},{1,1,1},{0,0,0},{0,1,0},{1,1,0},{0,1,0},{0,0,0},{1,1,1},{0,1,0},
{0,1,0},{0,1,1},{0,1,0},{0,1,0},{1,1,1},{0,1,0}};//先将每种字符代表的管道用矩阵表
int i,j,k;
char s[60][60];
while(scanf("%d%d",&m,&n)!=EOF)
{
if(m==(-1)&&n==-1)
break;
memset(a,0,sizeof(a));
memset(s,0,sizeof(s));
for(i=1;i<=m;i++)
scanf("%s",s[i]);
int x,y;
for(i=1;i<=m;i++)
{
for(j=0;j<n;j++)
{
x=(i-1)*3;
// y=(j+1)*x;
for(k=(s[i][j]-'A')*3;k<(s[i][j]-'A'+1)*3;k++)//构图
{
// printf("s===%c k====%d\n",s[i][j],k);
a[x][j*3]=t[k][0];
a[x][j*3+1]=t[k][1];
a[x][j*3+2]=t[k][2];
x++;
}
}
}
int sum=0;
for(i=0;i<m*3;i++)
{
for(j=0;j<n*3;j++)
{
if(a[i][j]==1)
{
dfs(i,j);//搜索
sum++;
}
}
}
printf("%d\n",sum);
}
return 0;
}


