Codeforces780C
题解:n个气球 从1到n染色,如果a、b和c是不同的正方形,a和b在它们之间有一条直接的路径,b和c之间有一条直接的路径,然后在这三个方块上的气球颜色是不同的。
AC代码
#include <stdio.h> #include <math.h> #include <string.h> #include <stdlib.h> #include <iostream> #include <sstream> #include <algorithm> #include <string> #include <queue> #include <vector> using namespace std; const int maxn= 200010; const int inf = 0x3f3f3f3f; typedef long long ll; int color[maxn]; std::vector<int> v[maxn]; int n,ans=0; void dfs(int now,int father) { int i,k; k=0; for(i=0; i<v[now].size(); i++) { if(color[v[now][i]]!=inf) { continue; //该点已经访问过,直接下一个邻接点 } k++; while(color[now]==k||color[father]==k) //确定颜色 { k++; } color[v[now][i]]=k; dfs(v[now][i],now); } ans=ans<k?k:ans; } int main(int argc, char const *argv[]) { int a,b; cin>>n; for(int i=0; i<n-1; i++) { cin>>a>>b; v[a].push_back(b); //存图的边 v[b].push_back(a); } memset(color,inf,sizeof(color)); color[0]=0; color[1]=1; dfs(1,0); cout<<ans<<endl; for(int i=1; i<n; i++) { cout<<color[i]<<" "; } cout<<color[n]<<endl; return 0; }
Andryusha goes through a park each day. The squares and paths between them look boring to Andryusha, so he decided to decorate them.
The park consists of n squares connected with (n - 1) bidirectional paths in such a way that any square is reachable from any other using these paths. Andryusha decided to hang a colored balloon at each of the squares. The baloons' colors are described by positive integers, starting from 1. In order to make the park varicolored, Andryusha wants to choose the colors in a special way. More precisely, he wants to use such colors that if a, b and c are distinct squares that a and b have a direct path between them, and b and c have a direct path between them, then balloon colors on these three squares are distinct.
Andryusha wants to use as little different colors as possible. Help him to choose the colors!
The first line contains single integer n (3 ≤ n ≤ 2·105) — the number of squares in the park.
Each of the next (n - 1) lines contains two integers x and y (1 ≤ x, y ≤ n) — the indices of two squares directly connected by a path.
It is guaranteed that any square is reachable from any other using the paths.
In the first line print single integer k — the minimum number of colors Andryusha has to use.
In the second line print n integers, the i-th of them should be equal to the balloon color on the i-th square. Each of these numbers should be within range from 1 to k.
3
2 3
1 3
3
1 3 2
5
2 3
5 3
4 3
1 3
5
1 3 2 5 4
5
2 1
3 2
4 3
5 4
3
1 2 3 1 2
In the first sample the park consists of three squares: 1 → 3 → 2. Thus, the balloon colors have to be distinct.
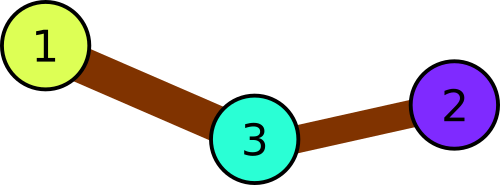 Illustration for the first sample.
Illustration for the first sample.In the second example there are following triples of consequently connected squares:
- 1 → 3 → 2
- 1 → 3 → 4
- 1 → 3 → 5
- 2 → 3 → 4
- 2 → 3 → 5
- 4 → 3 → 5
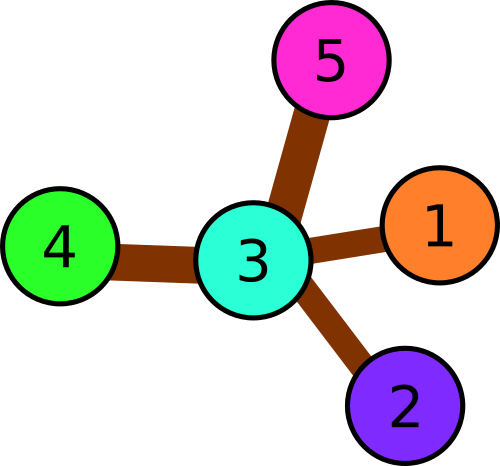 Illustration for the second sample.
Illustration for the second sample.In the third example there are following triples:
- 1 → 2 → 3
- 2 → 3 → 4
- 3 → 4 → 5
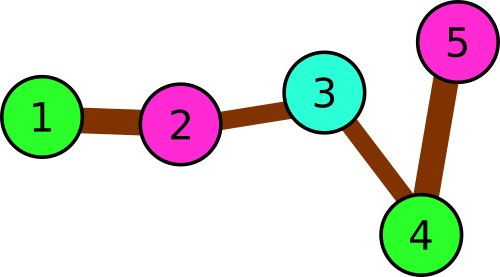 Illustration for the third sample.
Illustration for the third sample.


