2-3树的插入和删除原理

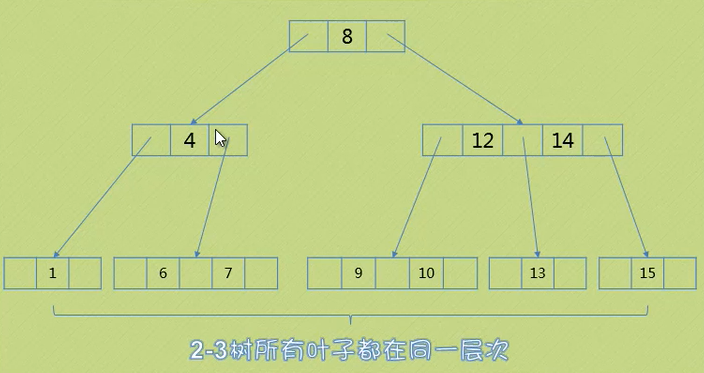
2-3树

多路查找树
2-节点，含有一个值和两条链接
3-节点，含有两个值和三条链接
所有叶子必须都在同一层次

插入原理

情况一 空树

创建一个二节点作为根节点即可

情况二 二节点的叶子节点

插入3: 直接插入,将该二节点变为三节点即可

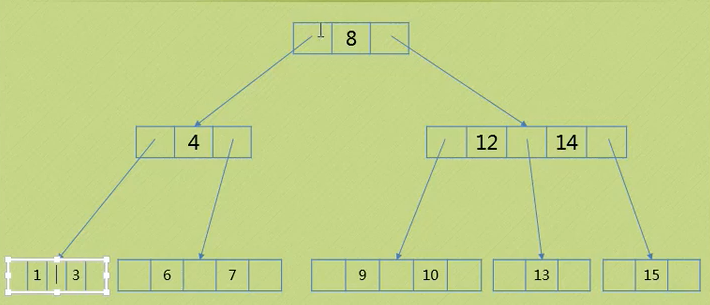
情况三 三节点的叶子节点 ( 父节点为二节点 )

插入5: 
1.根据左小右大,5应该插到6的左边,但是6所在的节点已经是三节点,且由于叶子节点必须要在同一层次(不能单独往下延伸)
2.不能够往下走,那就只能往上走,且父节点是二节点可扩展为三节点
3.将扩展节点的右节点的最左元素6上移,调整叶子节点(结果如图)

情况四 三节点的叶子节点 ( 父节点为三节点 )

插入11:
1.根据数值应该插入到10的右边,但10所在的节点已经为三节点了,同时其父节点也为三节点
2.继续往上找,父节点的父节点为二节点可扩展
3.将扩展的节点的右节点的最左元素12上移
4.9,10,11按照中序遍历的方式调整

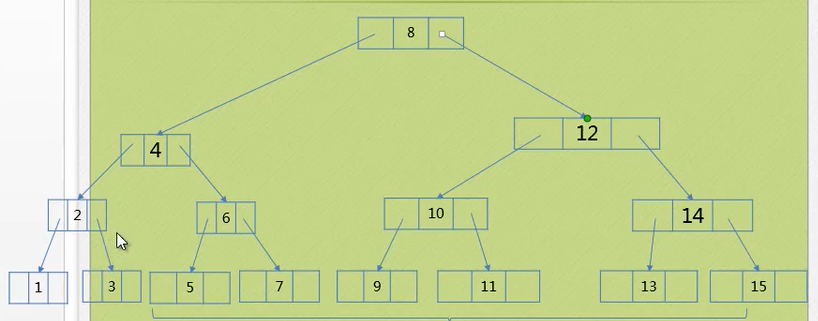
情况五 三节点的叶子节点 ( 父节点及其以上均为三节点 )

插入2:
1.按照数值大小,应该插入到1的右边,但1所在节点及其上面的所有节点都是三节点了,挤不下了,这时候就要增加高度了
2.从下往上拆,最后全部节点都变为二节点

删除原理

情况一 删除元素所在节点是三节点

直接删除,将三节点变为二节点即可

情况二 删除元素位于二节点 ( 父节点为二节点 , 右孩子为三节点)

删除1:
1.删掉1
2.左旋转,将4放到1所在的位置,6放到4所在的位置

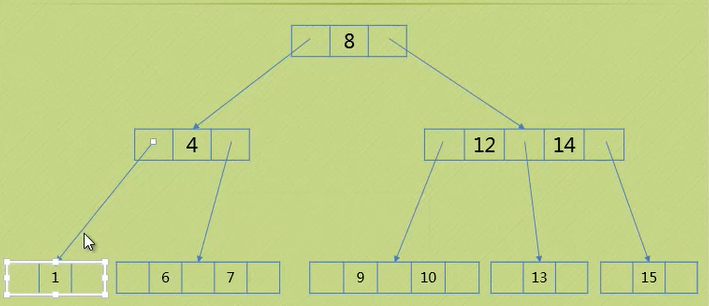
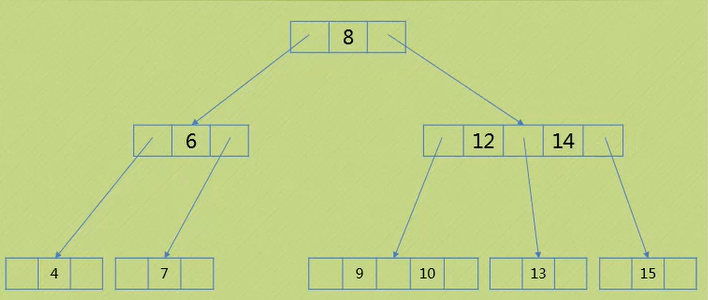
情况三 删除元素位于二节点 ( 父节点为二节点 , 右孩子也为二节点)

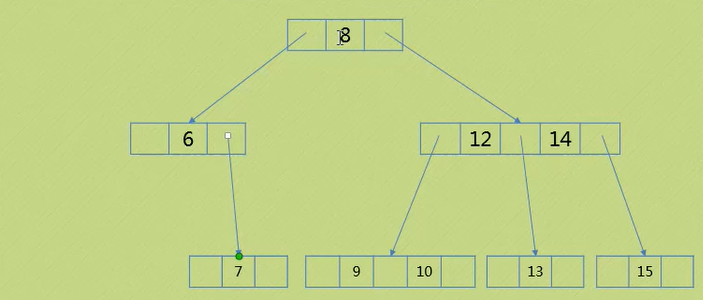
删除4:
1.首先要知道一点:图中7是根节点的直接前继,根节点的直接后继则是9
2.将后继9拿过来帮忙,放到8的位置,8则去左边帮忙,放到7的位置(本质也是左旋)
3.6,7也左旋调整

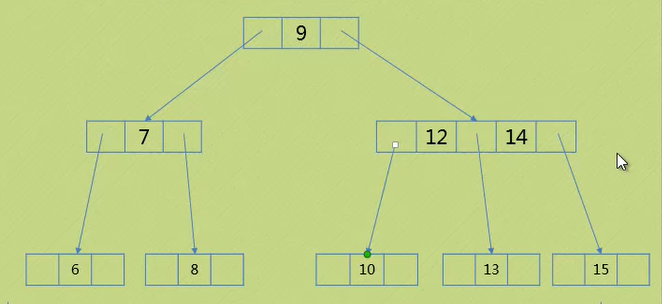
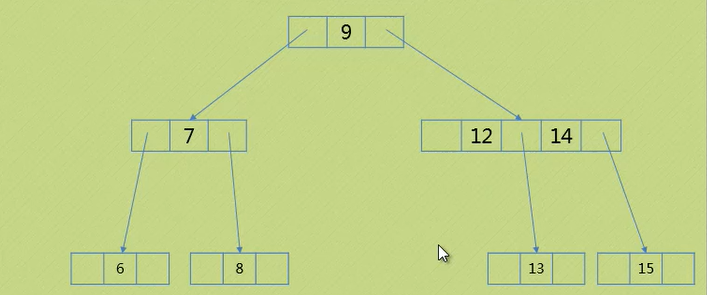
情况四 删除元素位于二节点 ( 父节点为三节点 )

删除10:
1.将父节点由三节点变为二节点
2.扩展原先父节点的中间节点

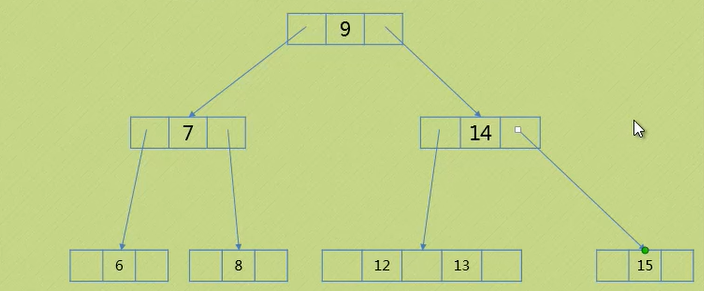
情况五 满二叉树的时候删除

如图,节点均为二节点
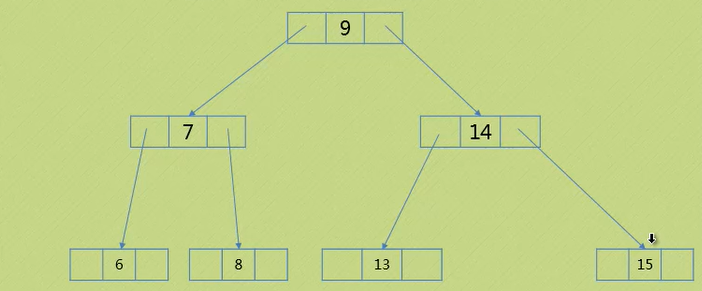
删除8:
1.思路与上面插入的情况五相反,所有节点都不能拆分了,那就扩大宽度缩小一层

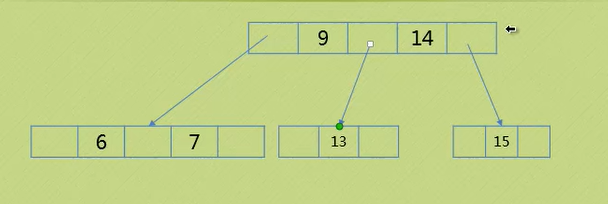
情况六 删除的节点不是叶子节点 ( 删除节点右孩子为三节点 )

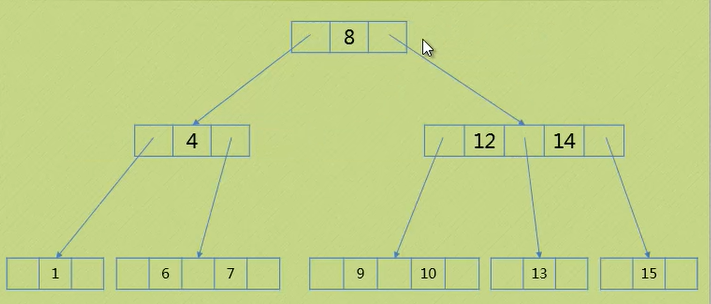
删除4:
1.右孩子最左元素上移即可
2.右孩子变为二节点

其余删除非叶子节点的情况处理方法类似,就不赘述了