HDCTF CRYPTO部分 wp

HDCTF CRYPTO部分 wp

Normal_Rsa(revenge)

from Crypto.Util.number import *
#from shin import flag


m=bytes_to_long(b'HDCTF{******}')
e=65537
p=getPrime(256)
q=getPrime(512)
r=getPrime(512)
n=p*q*r
P=pow(p,2,n)
Q=pow(q,2,n)
c=pow(m,e,n)
print(f"P = {P}")
print(f"Q = {Q}")
print(f"n = {n}")
print(f"c = {c}")
'''
P = 8760210374362848654680470219309962250697808334943036049450523139299289451311563307524647192830909610600414977679146980314602124963105772780782771611415961
Q = 112922164039059900199889201785103245191294292153751065719557417134111270255457254419542226991791126571932603494783040069250074265447784962930254787907978286600866688977261723388531394128477338117384319760669476853506179783674957791710109694089037373611516089267817074863685247440204926676748540110584172821401
n = 12260605124589736699896772236316146708681543140877060257859757789407603137409427771651536724218984023652680193208019939451539427781667333168267801603484921516526297136507792965087544395912271944257535087877112172195116066600141520444466165090654943192437314974202605817650874838887065260835145310202223862370942385079960284761150198033810408432423049423155161537072427702512211122538749
c = 7072137651389218220368861685871400051412849006784353415843217734634414633151439071501997728907026771187082554241548140511778339825678295970901188560688120351732774013575439738988314665372544333857252548895896968938603508567509519521067106462947341820462381584577074292318137318996958312889307024181925808817792124688476198837079551204388055776209441429996815747449815546163371300963785
'''

主要是知识点是 p**2%n 3个素数 e和phi不互素

脚本如下

import libnum
import gmpy2

e=  65537
P = 8760210374362848654680470219309962250697808334943036049450523139299289451311563307524647192830909610600414977679146980314602124963105772780782771611415961
Q = 112922164039059900199889201785103245191294292153751065719557417134111270255457254419542226991791126571932603494783040069250074265447784962930254787907978286600866688977261723388531394128477338117384319760669476853506179783674957791710109694089037373611516089267817074863685247440204926676748540110584172821401
n = 12260605124589736699896772236316146708681543140877060257859757789407603137409427771651536724218984023652680193208019939451539427781667333168267801603484921516526297136507792965087544395912271944257535087877112172195116066600141520444466165090654943192437314974202605817650874838887065260835145310202223862370942385079960284761150198033810408432423049423155161537072427702512211122538749
c = 7072137651389218220368861685871400051412849006784353415843217734634414633151439071501997728907026771187082554241548140511778339825678295970901188560688120351732774013575439738988314665372544333857252548895896968938603508567509519521067106462947341820462381584577074292318137318996958312889307024181925808817792124688476198837079551204388055776209441429996815747449815546163371300963785

p1,s=gmpy2.iroot(P,2)
q,s=gmpy2.iroot(Q,2)
p=libnum.nroot(P,2)
q=libnum.nroot(Q,2)
p=gmpy2.gcd(P,n)
q=gmpy2.gcd(Q,n)
p=libnum.gcd(P,n)
q=libnum.gcd(Q,n)
t=n//(p*q)

phi=(p-1)*(q-1)*(t-1)
a1=libnum.gcd(e,phi)
a2=e//a1
d=libnum.invmod(a2,phi)
m1=pow(c,d,n)
m=libnum.nroot(m1,a1)
print(libnum.n2s(m))

也可以通过工具来解密————轩禹CTF_RSA工具3.6

爬过小山去看云

题目如下

密文：ymyvzjtxswwktetpyvpfmvcdgywktetpyvpfuedfnzdjsiujvpwktetpyvnzdjpfkjssvacdgywktetpyvnzdjqtincduedfpfkjssne
在山的那头，有3个人，4只鸟，19只羊，11朵云

题目提示小山，小山的英文是hill，所以是希尔(Hill Cipher)密码，然后进行解密

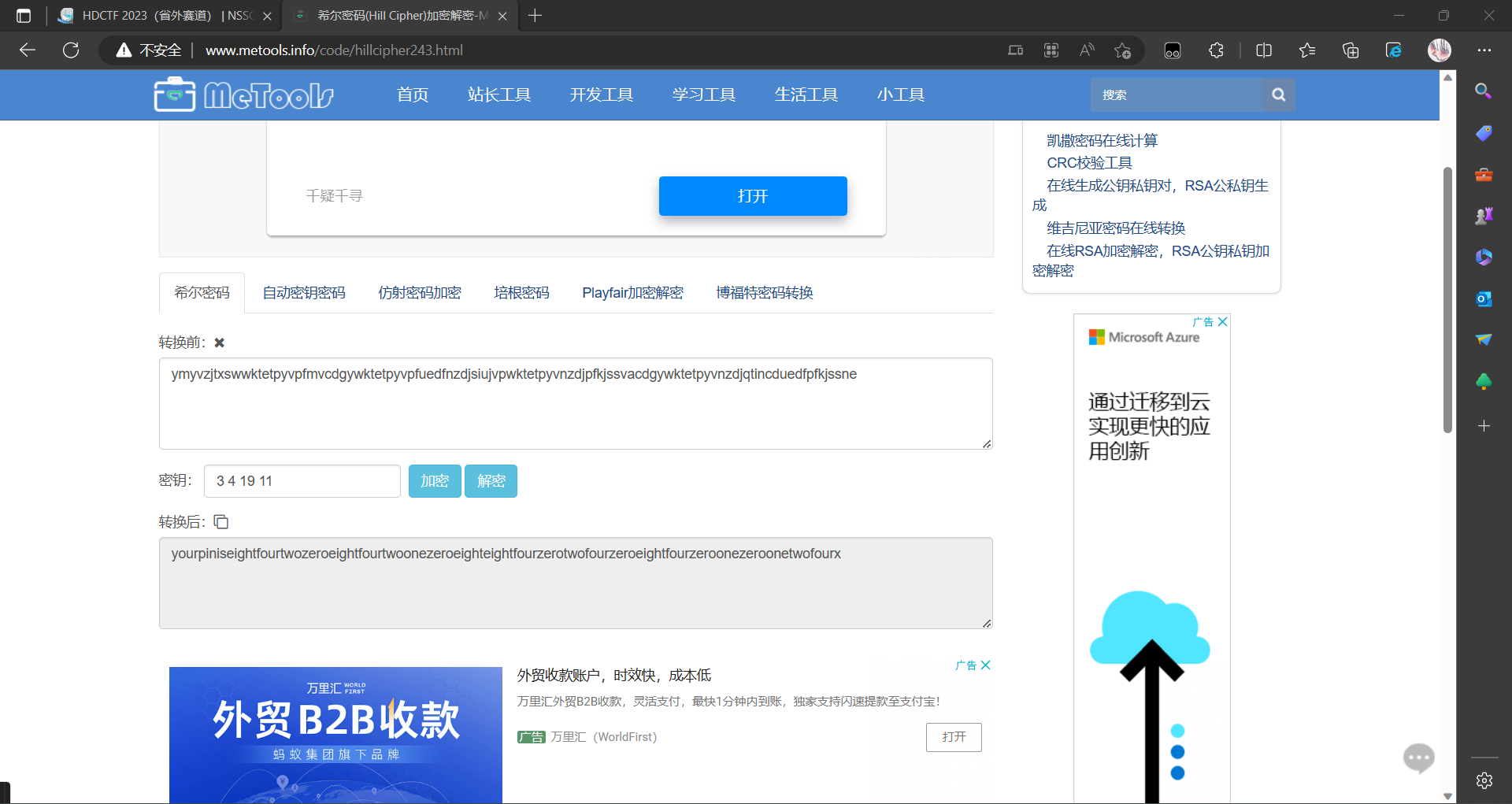
然后英文转数字为842084210884024084010124，题目中提示了云，那就是云影密码解密

Math_Rsa

题目内容

from Crypto.Util.number import *
from shin import flag


m=bytes_to_long(flag)
r=getPrime(1024)
assert r%4==3
p=getPrime(1024)
assert pow(p,(r-1)//2,r)==1
q=getPrime(1024)
e=65537
n=p*q
a=pow(p,2,r)
c=pow(m,e,n)
print(f"n = {n}")
print(f"r = {r}")
print(f"a = {a}")
print(f"c = {c}")
'''
n = 14859096721972571275113983218934367817755893152876205380485481243331724183921836088288081702352994668073737901001999266644597320501510110156000004121260529706467596723314403262665291609405901413014268847623323618322794733633701355018297180967414569196496398340411723555826597629318524966741762029358820546567319749619243298957600716201084388836601266780686983787343862081546627427588380349419143512429889606408316907950943872684371787773262968532322073585449855893701828146080616188277162144464353498105939650706920663343245426376506714689749161228876988380824497513873436735960950355105802057279581583149036118078489
r = 145491538843334216714386412684012043545621410855800637571278502175614814648745218194962227539529331856802087217944496965842507972546292280972112841086902373612910345469921148426463042254195665018427080500677258981687116985855921771781242636077989465778056018747012467840003841693555272437071000936268768887299
a = 55964525692779548127584763434439890529728374088765597880759713360575037841170692647451851107865577004136603179246290669488558901413896713187831298964947047118465139235438896930729550228171700578741565927677764309135314910544565108363708736408337172674125506890098872891915897539306377840936658277631020650625
c = 12162333845365222333317364738458290101496436746496440837075952494841057738832092422679700884737328562151621948812616422038905426346860411550178061478808128855882459082137077477841624706988356642870940724988156263550796637806555269282505420720558849717265491643392140727605508756229066139493821648882251876933345101043468528015921111395602873356915520599085461538265894970248065772191748271175288506787110428723281590819815819036931155215189564342305674107662339977581410206210870725691314524812137801739246685784657364132180368529788767503223017329025740936590291109954677092128550252945936759891497673970553062223608
'''

解题脚本

#根据质数 r 计算 a = p^2 mod r；
#计算 φ(n) = (p-1)(q-1)；
#计算 e 在模 φ(n) 意义下的逆元 d，即满足 e * d ≡ 1 (mod φ(n)) 的最小正整数 d；
#计算明文 m = c^d mod n。


from Crypto.Util.number import *
# 密文 c、模数 n 和加密指数 e，这里使用与加密相同的参数
c = 12162333845365222333317364738458290101496436746496440837075952494841057738832092422679700884737328562151621948812616422038905426346860411550178061478808128855882459082137077477841624706988356642870940724988156263550796637806555269282505420720558849717265491643392140727605508756229066139493821648882251876933345101043468528015921111395602873356915520599085461538265894970248065772191748271175288506787110428723281590819815819036931155215189564342305674107662339977581410206210870725691314524812137801739246685784657364132180368529788767503223017329025740936590291109954677092128550252945936759891497673970553062223608
n = 14859096721972571275113983218934367817755893152876205380485481243331724183921836088288081702352994668073737901001999266644597320501510110156000004121260529706467596723314403262665291609405901413014268847623323618322794733633701355018297180967414569196496398340411723555826597629318524966741762029358820546567319749619243298957600716201084388836601266780686983787343862081546627427588380349419143512429889606408316907950943872684371787773262968532322073585449855893701828146080616188277162144464353498105939650706920663343245426376506714689749161228876988380824497513873436735960950355105802057279581583149036118078489
e = 65537
a=55964525692779548127584763434439890529728374088765597880759713360575037841170692647451851107865577004136603179246290669488558901413896713187831298964947047118465139235438896930729550228171700578741565927677764309135314910544565108363708736408337172674125506890098872891915897539306377840936658277631020650625
# 根据质数 r 计算 a = p^2 mod r
r = 145491538843334216714386412684012043545621410855800637571278502175614814648745218194962227539529331856802087217944496965842507972546292280972112841086902373612910345469921148426463042254195665018427080500677258981687116985855921771781242636077989465778056018747012467840003841693555272437071000936268768887299
p = pow(a, (r+1)//4, r)

# 计算 φ(n) = (p-1)(q-1)，并计算 e 在模 φ(n) 意义下的逆元 d
phi = (p-1)*(n//p-1)
d = inverse(e, phi)

# 计算明文 m = c^d mod n
m = pow(c, d, n)
print(long_to_bytes(m))

计算得到

flag为HDCTF{0ce04f81-516b-4132-81a2-b0b7166e03ad}