[BZOJ1135][P3488][POI2009]LYZ[线段树+Hall定理]

首先从二分图匹配的角度来想这个题，只要每个人都能和一双鞋子匹配，那么溜冰鞋就是足够的。

但看范围不能用二分图匹配来做，因为边数会爆炸

Hall定理是判定二分图是否存在完全匹配的定理。

完全匹配：是指最大匹配数为 \(min(|X|,|Y|)\) 也就是 \(X\) 或 \(Y\) 集合其中一个集合所有点都被匹配了。

设二分图\(G=\lt V\text{1,}V\text{2,}E\gt\)中 \(|V\text{1|}=m<=|V\text{2|}=n\)
, \(G\) 中存在从 \(V1\)到 \(V2\) 的完全匹配当且仅当 \(V1\) 中任意 \(k(k=1,2,...,m)\) 个顶点至少与 \(V2\) 中 \(k\) 个顶点是相邻的。
有解的条件就是任意一个人的集合的人数<=所连接的鞋子数量

当\(r_i\)是连续的时候连接的鞋子的数量最少。


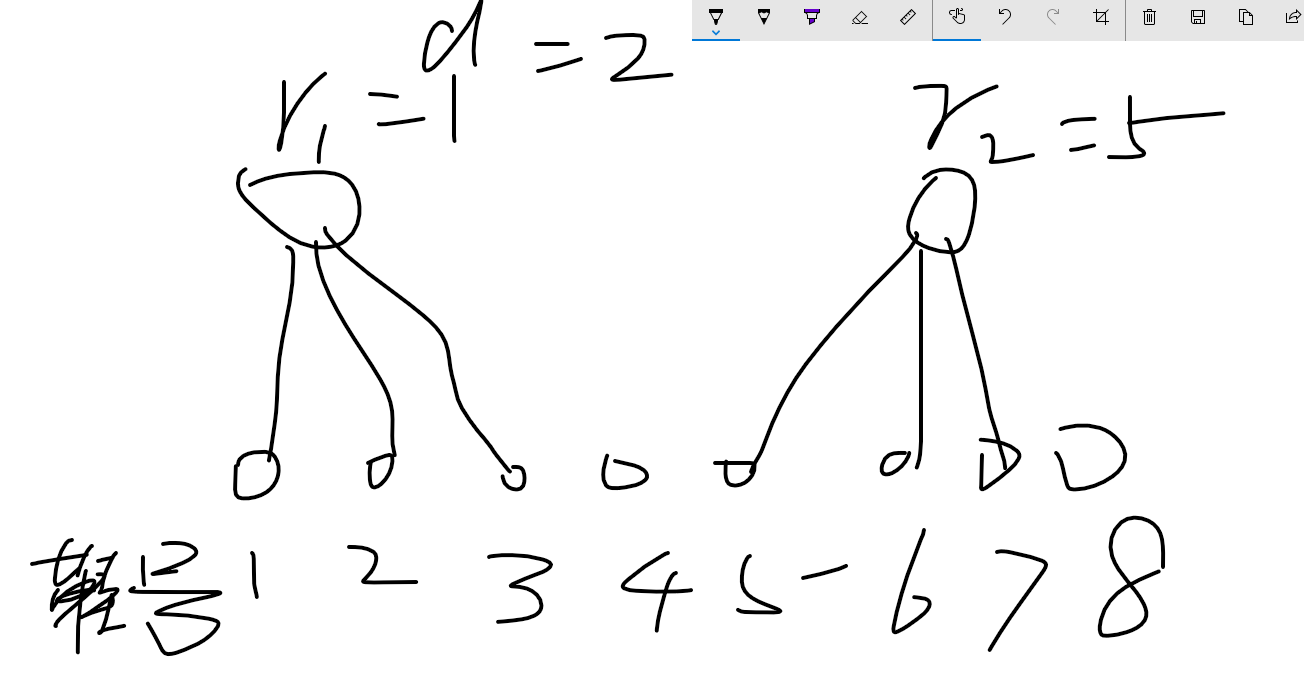
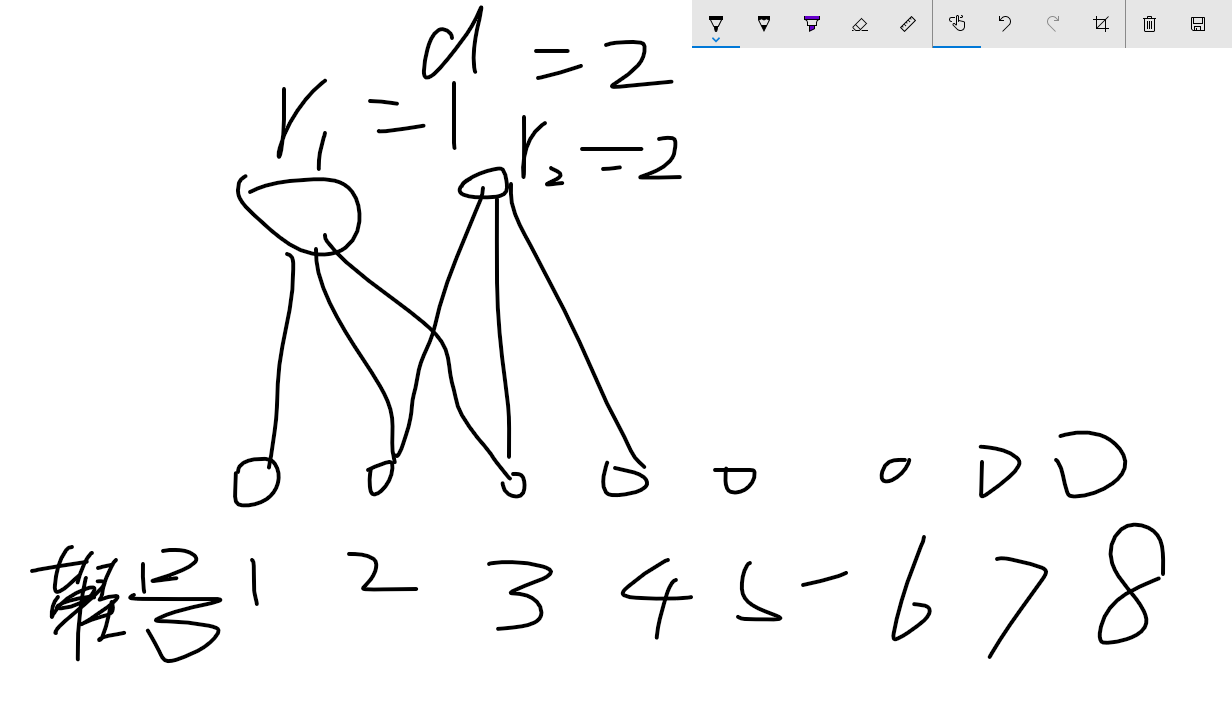
所以如果连续的情况满足，其他情况一定满足。

关于为什么最坏情况不满足，其他情况就一定不满足，不是很懂，翻了好多题解都没有看到关于这个的解释。求解

上述成立的话，就是带修改维护最大子段和了

\[\sum_{i=l}^r{\{}a\left[ i \right] \le \,\,\left( r-l+1+d \right) *k\} \]

\[\sum_{i=l}^r{\left( a\left[ i \right] -k \right) \le d*k} \]

#include <map>
#include <set>
#include <list>
#include <cmath>
#include <ctime>
#include <queue>
#include <deque>
#include <stack>
#include <bitset>
#include <cctype>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
 
bool Debug;
 
const int mod = 1e9+7;
const int MAXN = 2e5+7;

#define xx first
#define yy second
#define pb push_back
#define mp make_pair
#define iter iterator
#define sqr(a) ((a)*(a))
#define abs(a) ((a)>0?(a):(-(a)))
#define max(a, b) ((a)>(b)?(a):(b))
#define min(a, b) ((a)<(b)?(a):(b))
#define mset(a, b) memset(a, b, sizeof(a))
#define mcpy(a, b) memcpy(a, b, sizeof(a))
#define lop(i,a,b) for(int i = (a); i <= (b); ++i)
#define dlop(i,a,b) for(int i = (a); i >= (b); --i)
#define debu(...) if (Debug) fprintf(stderr, __VA_ARGS__)
#define debug(x) if (Debug) cerr << "" #x " = " << x << endl
#define ergo(a) for(auto it = a.begin(); it != a.end(); ++it)
 
template<typename T> T gcd(T a, T b) {T t; while(t = a % b) a = b, b = t; return b;}
template<typename T> T Pow(T a, T b, T mod) {T ret = 1; for( ; b; b >>= 1) {if (b & 1) ret = ret * 1ull * a % mod; a = a * 1ull * a % mod;} return ret%mod;}
template<typename T> void chmax(T &x, T y) {if (x < y) x = y;}
template<typename T> void chmin(T &x, T y) {if (x > y) x = y;}
template<typename T> void amod(T &x, T y) {x += y; if (x >= mod) x -= mod;}
template<typename T> void smod(T &x, T y) {x -= y; if (x < 0) x += mod;}
 
typedef long long ll; 
typedef long double ld;
typedef unsigned int uint;
typedef pair<int,int> pii;
typedef unsigned long long ull;
template<typename T> void read(T &x) {
  x = 0; int c = getchar(), f = 1;
  while(!isdigit(c)) (c=='-')&&(f = -1), c = getchar();
  while(isdigit(c)) x = x * 10 + c - '0', c = getchar();
  x *= f;
}
#define read2(a, b) read(a), read(b)
ll n, a[200005], m, k, d, x, y;
 
struct Node{
  ll lmax, rmax, tmax, val;
  Node *ls, *rs;
  inline void pushup(){
    val = ls->val + rs->val;
    lmax = max(ls->lmax, ls->val + rs->lmax);
    rmax = max(rs->rmax, rs->val + ls->rmax);
    tmax = max(ls->tmax, max(rs->tmax, ls->rmax + rs->lmax));
  }
}pool[MAXN<<1], *root;
inline Node *newNode() {
  static int cnt = 0;
  return &pool[cnt++];
}
 
Node *build(int l, int r) {
  Node *cur = newNode();
  if (l != r) {
    int mid = l+r>>1;
    cur->ls = build(l, mid);
    cur->rs = build(mid+1, r);
    cur->pushup();
  }
  else cur->val = cur->tmax = -k;
  return cur;
}
 
void Modify(Node *cur, int l, int r, int x, int y) {
  if (l == r) {
    cur->val += y, cur->tmax += y; 
    cur->lmax = cur->rmax = max(cur->val, 0);
    return ;
  }
  int mid = l+r>>1;
  if (x <= mid) Modify(cur->ls, l, mid, x, y);
  else Modify(cur->rs, mid+1, r, x, y);
  cur->pushup();
}
 
int main() {
  #ifdef LOCAL_DEBUG
    Debug = 1;
    // freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
  #endif
  read2(n, m), read2(k, d);
  root = build(1, n);
  while(m--) {
    read2(x, y);
//    cerr << x << ' ' << y << endl;
    Modify(root, 1, n, x, y);
    if (root->tmax <= k * d) puts("TAK");
    else puts("NIE");
  }
//  cout << root->tmax;
  return 0;
}