[BZOJ4448][SCOI2015]情报传递[dfs序+树状数组]

2操作可以转化成x的权值在i时刻变成了1，然后查询的操作相当于查询i - c[i] 时刻 x->y链上权值和

可以差分成 $$f(x) + f(y) - f(\text{lca}) - f(fa[lca])$$

f是指根到一个点链上的权值和

这个可以直接写成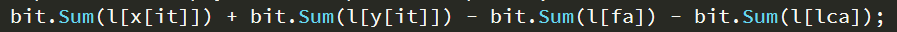

x子树中跟链无关的点会抵消掉（x子树中的所有点dfs序的左端点和右端点都被x的dfs序包含 +1的位置和-1的位置都被覆盖了，所以会抵消）

（那个add(l[x[i]] + siz[x[i]], -1)后来被我改成remove了

第一个查询就是查询链长而已。。

复杂度$$O(mlogn)$$

#include <bits/stdc++.h>
using namespace std;
 
typedef double lf;
typedef long long ll;
typedef long double llf;
typedef pair<ll, ll> pll;
typedef unsigned int uint;
typedef pair<int, int> pii;
typedef unsigned long long ull;
 
bool Debug;
const int mod = 1e9 + 7, MAXN = 2e5 + 7, inft = 1e9;
const ll infl = 1ll << 60;
 
#define xx first
#define yy second
#define pb push_back
#define mp make_pair
#define mset(a, b) memset(a, b, sizeof(a))
#define debug(...) if (Debug) fprintf(stderr, __VA_ARGS__)
#define lop(i,a,b) for(int i = (a), i##end = (b); i <= i##end; ++i)
#define dlop(i,a,b) for(int i = (a), i##end = (b); i >= i##end; --i)
#define ergo(a) for(__typeof(a.end())it = (a).begin(), it##end = (a).end(); it != it##end; ++it)
 
template<class A, class B> inline void chmax(A &x, B y) {if (x < y) x = y;}
template<class A, class B> inline void chmin(A &x, B y) {if (x > y) x = y;}
template<class A, class B> inline A max(A a, B b) {return a > b ? a : b;}
template<class A, class B> inline A min(A a, B b) {return a < b ? a : b;}
template<class A, class B> inline A gcd(A a, B b) {if (a < b) swap(a, b); if (!b) return a; while (A t = a % b) a = b, b = t; return b;}
template<class A, class B> inline A lcm(A a, B b) {return a / gcd(a, b) * b;}
template<class A, class B> inline A Pow(A a, B b) {A ret; for (ret = 1; b; b >>= 1) {if (b & 1) ret = ret * 1ll * a % mod; a = a * 1ll * a % mod;} return ret % mod;}
template<class T> inline T abs(T x) {return x >= 0 ? x : -x;}
template<class T> inline T sqr(T x) {return x * x;}
 
struct IO {
  struct Cg {inline int operator()() {return getchar();}};
  struct Cp {inline void operator()(int x) {putchar(x);}};
#define IS(x) (x == 10 || x == 13 || x == ' ')
#define OP operator
#define RT return *this
#define RX x=0;int t=P();while((t<'0'||t>'9')&&t!='-')t=P();f=1;\
if(t=='-')t=P(),f=-1;x=t-'0';for(t=P();t>='0'&&t<='9';t=P())x=x*10+t-'0'
#define RL if(t=='.'){lf u=0.1;for(t=P();t>='0'&&t<='9';t=P(),u*=0.1)x+=u*(t-'0');}if(f==-1)x=-x;
#define RU x=0;int t=P();while(t<'0'||t>'9')t=P();x=t-'0';for(t=P();t>='0'&&t<='9';t=P())x=x*10+t-'0'
#define TR *this,x;return x
  template<typename T>struct Fr {int f; T P; inline Fr&OP, (int&x) {RX; x *= f; RT;} inline OP int() {int x; TR;} inline Fr&OP, (ll &x) {RX; x *= f; RT;} inline OP ll() {ll x; TR;} inline Fr&OP, (char&x) {for (x = P(); IS(x); x = P()); RT;} inline OP char() {char x; TR;} inline Fr&OP, (char*x) {char t = P(); for (; IS(t); t = P()); if (~t) {for (; !IS(t) && ~t; t = P()) * x++ = t;}*x++ = 0; RT;} inline Fr&OP, (lf&x) {RX; RL; RT;} inline OP lf() {lf x; TR;} inline Fr&OP, (llf&x) {RX; RL; RT;} inline OP llf() {llf x; TR;} inline Fr&OP, (uint&x) {RU; RT;} inline OP uint() {uint x; TR;} inline Fr&OP, (ull&x) {RU; RT;} inline OP ull() {ull x; TR;}};
  Fr<Cg>in;
#define WI if(x){if(x<0)P('-'),x=-x;c=0;while(x)s[c++]=x%10+'0',x/=10;while(c--)P(s[c]);}else P('0')
#define WL if(y){lf t=0.5;for(int i=y;i--;)t*=0.1;if(x>=0)x+=t;else x-=t,P('-');*this,(ll)(abs(x));P('.');if(x<0)\
x=-x;while(y--){x*=10;x-=floor(x*0.1)*10;P(((int)x)%10+'0');}}else if(x>=0)*this,(ll)(x+0.5);else *this,(ll)(x-0.5);
#define WU if(x){c=0;while(x)s[c++]=x%10+'0',x/=10;while(c--)P(s[c]);}else P('0')
  template<typename T>struct Fw {int c, s[24]; T P; inline Fw&OP, (int x) {WI; RT;} inline Fw&OP()(int x) {WI; RT;} inline Fw&OP, (uint x) {WU; RT;} inline Fw&OP()(uint x) {WU; RT;} inline Fw&OP, (ll x) {WI; RT;} inline Fw&OP()(ll x) {WI; RT;} inline Fw&OP, (ull x) {WU; RT;} inline Fw&OP()(ull x) {WU; RT;} inline Fw&OP, (char x) {P(x); RT;} inline Fw&OP()(char x) {P(x); RT;} inline Fw&OP, (const char*x) {while (*x)P(*x++); RT;} inline Fw&OP()(const char*x) {while (*x)P(*x++); RT;} inline Fw&OP()(lf x, int y) {WL; RT;} inline Fw&OP()(llf x, int y) {WL; RT;}};
  Fw<Cp>out;
} io;
#define in io.in
#define out io.out
 
struct Edge {
  int v, next;
} G[MAXN]; int head[MAXN], son[MAXN], dep[MAXN], anc[MAXN], tot, l[MAXN], idx, ans1[MAXN], ans2[MAXN], s, n, m, x[MAXN], y[MAXN], c[MAXN], op, p, siz[MAXN], top[MAXN], k; 
 
inline void add(int u, int v) {
  G[++tot] = (Edge) {v, head[u]}; head[u] = tot;
}
 
#define cur G[i].v
void dfs1(int u) {
  dep[u] = dep[anc[u]] + 1, siz[u] = 1;
  for (int i = head[u]; i; i = G[i].next) {    
    dfs1(cur);
    siz[u] += siz[cur];
    if (siz[cur] >= siz[son[u]]) son[u] = cur;
  }
}
void dfs2(int u, int t) {
  top[u] = t; l[u] = ++idx;
  if (son[u]) dfs2(son[u], t);
  for(int i = head[u]; i; i = G[i].next) if (cur != son[u]) dfs2(cur, cur);
}
#undef cur
inline int LCA(int u, int v) {
  while(top[u] != top[v]) 
    dep[top[u]] >= dep[top[v]] ? u = anc[top[u]] : v = anc[top[v]];
  return dep[u] < dep[v] ? u : v;
}
vector<int>q[MAXN];
struct BIT {
  int t[MAXN];
  inline void add(register int k) {
    while (k <= n) ++t[k], k += k & (-k);
  }
  inline void remove(register int k) {
    while (k <= n) --t[k], k += k & (-k);
  }
  inline int Sum(int k) {
    register int ret = 0;
    while (k) ret += t[k], k -= k & (-k);
    return ret;
  }
} bit;
 
int main() {
  in, n;
  lop(i, 1, n) {
    in, anc[i];
    if (!anc[i]) s = i;
    else add(anc[i], i);
  }
  dfs1(s), dfs2(s, s);
  in, m;
  lop(i, 1, m) {
    in, k, x[i];
    if (k == 1) {
      in, y[i], c[i];
      c[i] = i - c[i];
      q[max(1, c[i])].pb(i);// c[i] <= 0 is equal to c[i] = 1 
    }
  }
  lop(i,1,m) {
    for(vector<int>::iterator it = q[i].begin(); it != q[i].end(); ++it) {
      int lca = LCA(x[*it], y[*it]), fa = anc[lca];
      ans1[*it] = dep[x[*it]] + dep[y[*it]] - dep[fa] - dep[lca];
      ans2[*it] = bit.Sum(l[x[*it]]) + bit.Sum(l[y[*it]]) - bit.Sum(l[fa]) - bit.Sum(l[lca]);
    }
    if (!y[i]) bit.add(l[x[i]]), bit.remove(l[x[i]] + siz[x[i]]);// the node M between l[x[i]] and l[x[i]] + siz[x[i]](M in x[i]'s subtree) will not influence the result because +1 and -1 = 0
  }
  lop(i,1,m) if (ans1[i]) out, ans1[i], ' ', ans2[i], '\n';
  return 0;
}