[BZOJ4870][SHOI2017]组合数问题[递推+矩阵快速幂]
题意:求
\[\sum_{i=1}^{ik+r\le n}{\text{C}^{ik+r}_{nk}}\left( \text{mod }p \right)
\]
发现实际上是求 \(\mod p \equiv r\) 的组合数之和
\(dp[i][j]\)表示从 \(i\) 个球中取 \(j\) 个的方案数 其中\(j\) 满足 \(j \equiv r \pmod k\)
所以\(dp[i][j] = dp[i-1][j-1 \pmod k] + dp[i-1][j]\)
可以用矩阵乘法来优化
struct Matrix {
int mat[51][53], x, y;
inline void init(int n, int m) {
x = n, y = m;
lop(i, 1, x) lop(j, 1, y) mat[i][j] = 0;
}
inline Matrix &operator *(const Matrix &rhs) const {
assert(x && y && rhs.x && y == rhs.x);
static Matrix ret; ret.init(x, rhs.y);
lop(i, 1, x)
lop(k, 1, y) if (mat[i][k])
lop(j, 1, rhs.y) {
ret.mat[i][j] += mat[i][k] * 1ll * rhs.mat[k][j] % mod;
if (ret.mat[i][j] >= mod) ret.mat[i][j] -= mod;
}
return ret;
}
inline void operator ^=(ll k) {
static Matrix ret; ret.init(x, y);
lop(i, 1, x) ret.mat[i][i] = 1;
while (k) {
if (k & 1) ret = ret * (*this);
*this = *this * (*this);
k >>= 1;
}
*this = ret;
}
} a, b;
int main() {
cin >> n >> mod >> k >> r;
a.init(1, k);
a.mat[1][1] = 1;
b.init(k, k);
lop(i,0,k-1) ++b.mat[i+1][i+1], ++b.mat[i+1][(i-1+k)%k+1];//if your code is b.mat[...][...] = 1, when k = 1, it will be wrong (you can see pascal's trangle 2 = 1 + 1 but not 2 = 1 + 0)
b ^= 1ll * n * k;
a = a * b;
cout << a.mat[1][r+1];
return 0;
}

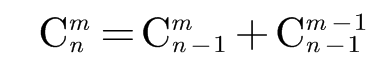

 浙公网安备 33010602011771号
浙公网安备 33010602011771号