舞蹈链DLX
算法
算法应用
主要用于精准覆盖问题,通过一点简单的改变就可以直接求重复覆盖问题。
算法流程
- 对于当前的矩阵,选择一行,将这一行和不能与这条边一起选的边上的所有点删掉。(不能一起选就是在同一列有点)
- 如果删掉后所有列都被删完了,就结束。
- 如果这时候还有列没被删,但没有行可以选了就说明不合法,开始回溯,将删去的边加回来。
总结:就是爆搜选的边,但是有一些优化剪枝,不能选矛盾的边。(看到这你会有一种云里雾里的感觉,不明白怎么快速实现,这是正常的,你只需要理解上面是正确的即可)
链表
上面的算法需要我们快速实现删除,回溯以及一些查询。我们考虑到链表是一种支持快速修改的结构,同时易于回溯(因为链表没有真正删除点,只是不经过它而已)。所以用链表实现上述操作。
所以我们引入十字交叉双向循环链表 ,看起来很高级,其实很简单,十字交叉是因为在两条链上,一条是行一条是列。双向就不用说了,循环是为了方便查找。(它就长下面这样子,图来自oi-wiki)
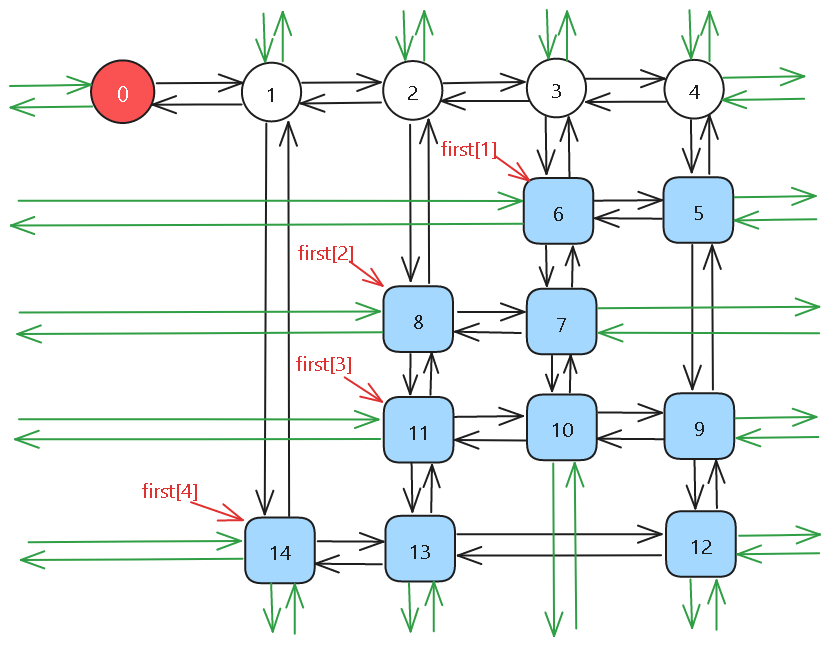
将一的信息存下来,为了方便寻找每一列的信息再多存一下列的编号。
代码实现
预处理&建模
void ycl()
{
for(int i=0;i<=m;i++)
{
dian[i].l=i-1;dian[i].r=i+1;
dian[i].u=i;dian[i].d=i;//有用,竖着的链也要首尾相连
lcnt[i]=0;//记录每列的1的个数
}
cnt=m;
dian[0].l=m,dian[cnt].r=0;//形成环
return ;
}
void addnode(int x,int y)
{
dian[++cnt].row=x;dian[cnt].col=y;//行列信息
dian[cnt].u=dian[y].u;dian[dian[y].u].d=cnt;
dian[cnt].d=y;dian[y].u=cnt;
if(!bk[x])//这一行的第一个1,bk[x]记录了第一个1的编号
{
dian[cnt].l=dian[cnt].r=cnt;//左右都没有点,自己成环
bk[x]=cnt;
}
else
{
dian[cnt].l=dian[bk[x]].l;dian[dian[bk[x]].l].r=cnt;
dian[cnt].r=bk[x];dian[bk[x]].l=cnt;
}
lcnt[y]++;//记录每列的1的个数
}
删除某一列及相关的东西
void del(int x)
{
for(int i=dian[x].d;i!=x;i=dian[i].d)//枚举在这一列是一的行,都要删除
{
for(int j=dian[i].r;j!=i;j=dian[j].r)//枚举删除的行上的列
{
dian[dian[j].u].d=dian[j].d;
dian[dian[j].d].u=dian[j].u;
lcnt[dian[j].col]--;
}
}
dian[dian[x].l].r=dian[x].r;
dian[dian[x].r].l=dian[x].l;//特殊处理列的编号所在的链
return ;
}
恢复某一列及相关的东西
与删除相反即可
void rev(int x)
{
dian[dian[x].l].r=x;
dian[dian[x].r].l=x;
for(int i=dian[x].d;i!=x;i=dian[i].d)//枚举删除的行
{
for(int j=dian[i].r;j!=i;j=dian[j].r)//枚举删除的行上的列
{
dian[dian[j].u].d=j;
dian[dian[j].d].u=j;
lcnt[dian[j].col]++;
}
}
return ;
}
dance!!!
bool dance(int dep)//搜索的层数
{
if(dian[0].r==0)//所有列都被合法删除,有解
{
for(int i=1;i<dep;i++)cout<<ans[i]<<' ';
cout<<'\n';
return 1;
}
int c=dian[0].r;
for(int i=c;i;i=dian[i].r)//在列的那条链上搜索
if(lcnt[i]<lcnt[c])c=i;//找最小的列,剪枝
del(c);//删除列c
for(int i=dian[c].d;i!=c;i=dian[i].d)//枚举选择的行
{
ans[dep]=dian[i].row;
for(int j=dian[i].r;j!=i;j=dian[j].r)//枚举删除的行上的列
del(dian[j].col);
if(dance(dep+1))return 1;
for(int j=dian[i].r;j!=i;j=dian[j].r)//恢复删除的行上的列
rev(dian[j].col);
}
rev(c);
return 0;
}
总代码
#include <bits/stdc++.h>
using namespace std;
const int N=50010;
int n,m,cnt,lcnt[N],bk[N],ans[N];
struct node
{
int l,r,u,d,row,col;//l,r,u,d分别表示左右上下节点编号,row,col表示所在行列
}dian[N];
void ycl()
{
for(int i=0;i<=m;i++)
{
dian[i].l=i-1;dian[i].r=i+1;
dian[i].u=i;dian[i].d=i;//是否有用?
lcnt[i]=0;//记录每列的1的个数
}
cnt=m;
dian[0].l=m,dian[cnt].r=0;//形成环
return ;
}
void addnode(int x,int y)
{
dian[++cnt].row=x;dian[cnt].col=y;
dian[cnt].u=dian[y].u;dian[dian[y].u].d=cnt;
dian[cnt].d=y;dian[y].u=cnt;
if(!bk[x])//这一行的第一个1,bk[x]记录了第一个1的编号
{
dian[cnt].l=dian[cnt].r=cnt;//左右都没有点,自己成环
bk[x]=cnt;
}
else
{
dian[cnt].l=dian[bk[x]].l;dian[dian[bk[x]].l].r=cnt;
dian[cnt].r=bk[x];dian[bk[x]].l=cnt;
}
lcnt[y]++;//记录每列的1的个数
}
void del(int x)
{
for(int i=dian[x].d;i!=x;i=dian[i].d)//枚举删除的行
{
for(int j=dian[i].r;j!=i;j=dian[j].r)//枚举删除的行上的列
{
dian[dian[j].u].d=dian[j].d;
dian[dian[j].d].u=dian[j].u;
lcnt[dian[j].col]--;
}
}
dian[dian[x].l].r=dian[x].r;
dian[dian[x].r].l=dian[x].l;
return ;
}
void rev(int x)
{
dian[dian[x].l].r=x;
dian[dian[x].r].l=x;
for(int i=dian[x].d;i!=x;i=dian[i].d)//枚举删除的行
{
for(int j=dian[i].r;j!=i;j=dian[j].r)//枚举删除的行上的列
{
dian[dian[j].u].d=j;
dian[dian[j].d].u=j;
lcnt[dian[j].col]++;
}
}
return ;
}
bool dance(int dep)//搜索的层数
{
if(dian[0].r==0)//所有列都被合法删除,有解
{
for(int i=1;i<dep;i++)cout<<ans[i]<<' ';
cout<<'\n';
return 1;
}
int c=dian[0].r;
for(int i=c;i;i=dian[i].r)//在列的那条链上搜索
if(lcnt[i]<lcnt[c])c=i;//找最小的列
del(c);//删除列c
for(int i=dian[c].d;i!=c;i=dian[i].d)//枚举删除的行
{
ans[dep]=dian[i].row;
for(int j=dian[i].r;j!=i;j=dian[j].r)//枚举删除的行上的列
del(dian[j].col);
if(dance(dep+1))return 1;
for(int j=dian[i].r;j!=i;j=dian[j].r)//恢复删除的行上的列
rev(dian[j].col);
}
rev(c);
return 0;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
ycl();//处理head和列号
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
int x;cin>>x;
if(x==1)addnode(i,j);//建节点
}
if(!dance(1))cout<<"No Solution!"<<'\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号