【洛谷P5470】序列
题目
题目链接:https://www.luogu.com.cn/problem/P5470
给定两个长度为 \(n\) 的正整数序列 \(\{a_i\}\) 与 \(\{b_i\}\),序列的下标为 \(1, 2, \cdots , n\)。现在你需要分别对两个序列各指定恰好 \(K\) 个下标,要求至少有 \(L\) 个下标在两个序列中都被指定,使得这 \(2K\) 个下标在序列中对应的元素的总和最大。
形式化地说,你需要确定两个长度为 \(K\) 的序列 \(\{c_i\}, \{d_i\}\),其中 \(1 \leq c_1 < c_2 <\cdots <c_K \leq n , 1 \leq d_1< d_2 < \cdots< d_K \leq n\),并要求 \(\{c_1, c_2, \cdots , c_K\} \cap \{d_1, d_2, · · · , d_K\}\geq L\)。
目标是最大化 \(\sum^{K}_{i=1} a_{c_i} +\sum^{K}_{i=1} b_{d_i}\)。
\(Q\leq 10;n\leq 2\times 10^5;\sum n\leq 10^6\)。
思路
考虑一个费用流模型:
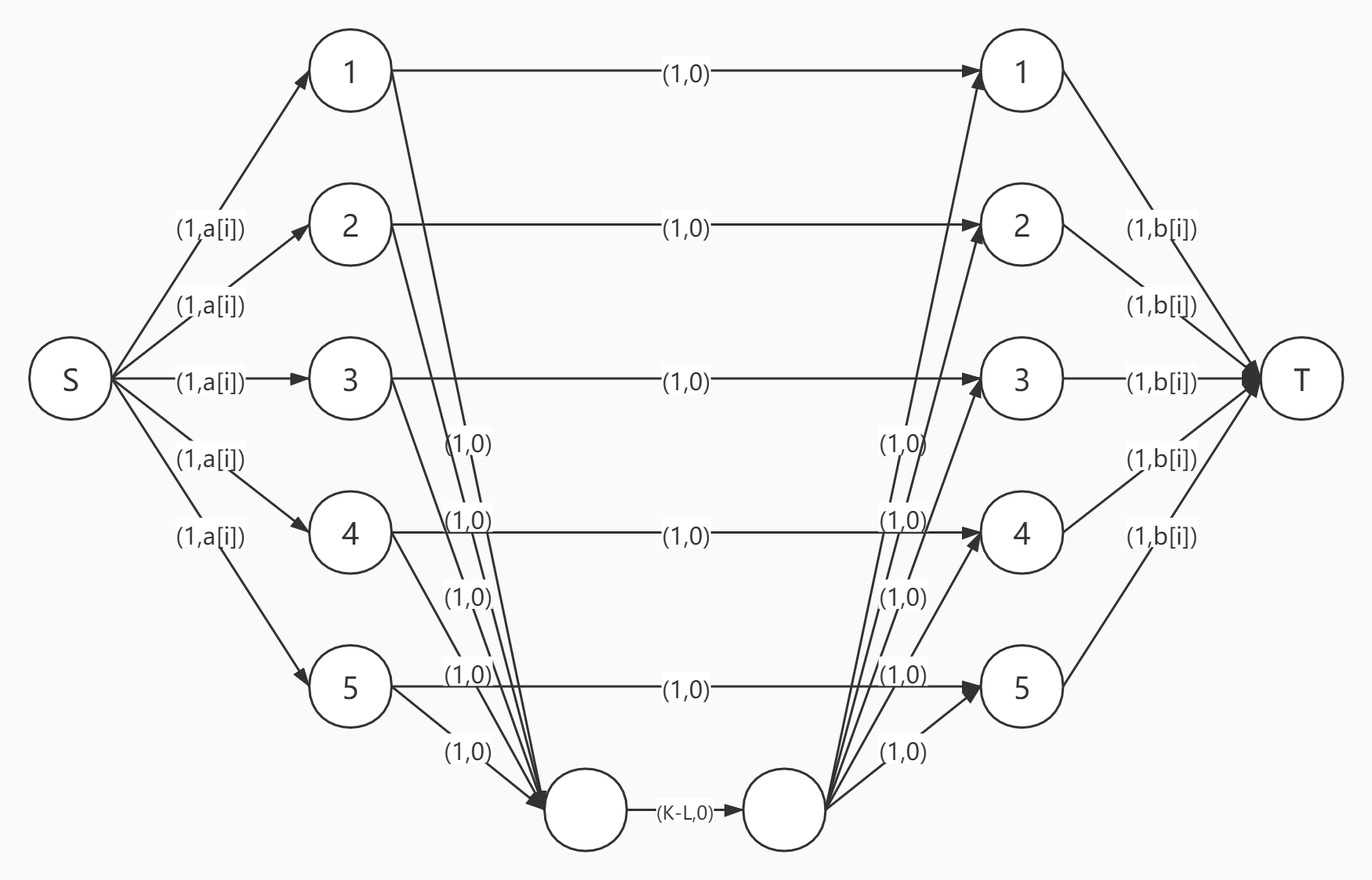
我们只需要求出流量为 \(K\) 的时候的最小费用即可。
采用 SPFA 找增广路即可做到 \(O(n^2K)\)。
我们称 \(a_i\) 和 \(b_j(i\neq j)\) 匹配为自由匹配,\(a_i\) 和 \(b_i\) 匹配为限制匹配。记 \(cnt\) 为剩余能自由匹配的次数,初始 \(cnt=K-L\)。
考虑模拟费用流:
- 如果 \(cnt>0\),显然此时进行自由匹配最优。取 \(a\) 中没有被匹配的最大值和 \(b\) 中没有被匹配的最大值匹配即可。
- 如果 \(cnt=0\),此时有以下三种匹配方式:
- 直接进行一次限制匹配,选择最大的 \(a_i+b_i\) 且 \(a_i,b_i\) 之前都没有匹配过的 \(i\) 进行匹配。
- 对于原来的一个匹配 \((a_i,b_j)\),且 \(b_i\) 没有匹配,那么选择一个最大的 \(a_k\) 且 \(a_k\) 没有匹配,然后取消 \((a_i,b_j)\) 这对匹配,增加 \((a_i,b_i),(a_k,b_j)\) 这对匹配。
- 对于原来的一个匹配 \((a_j,b_i)\),且 \(a_i\) 没有匹配,那么选择一个最大的 \(b_k\) 且 \(b_k\) 没有匹配,然后取消 \((a_j,b_i)\) 这对匹配,增加 \((a_i,b_i),(a_j,b_k)\) 这对匹配。
显然当 \(cnt=0\) 时,三中策略都不会使得 \(cnt\) 减小。选择三中策略中贡献最大的即可。因为模拟费用流中退流类似一个反悔贪心,只需要关心局部最优解即可。
具体的话,我们维护五个堆 \(qa,qb,qc,pa,pb\),分别表示 \(a\) 没被匹配的最大值;\(b\) 没被匹配的最大值;\(a_i,b_i\) 都没被匹配时 \(a_i+b_i\) 的最大值;\(b_i\) 被匹配,\(a_i\) 没被匹配时 \(a_i\) 的最大值;\(a_i\) 被匹配,\(b_i\) 没被匹配时 \(b_i\) 的最大值。
再维护 \(ma[i],mb[i]\) 表示 \(a_i\) 匹配的对象的下标;\(b_i\) 匹配的对象的下标。
当我们进行一次操作之后,需要分别维护好五个堆,两个数组以及 \(cnt\)。其实不难发现 \(qa,qb,qc\) 都不会增加元素,所以只需要考虑 \(pa,pb\) 增加元素的情况。
接下来就是一些细节了:
- \(cnt>0\) 时,如果选出的两个下标相等,那么不需要将 \(cnt\) 减一,当做限制匹配即可。
- \(cnt=0\) 时,策略 \(2,3\) 可能导致 \(cnt\) 加一。具体的,当 \(j=k\) 的时候相当于原先一组自由匹配变成了两组限制匹配,此时 \(cnt\) 需要加一。
- 当我们进行一次自由匹配时,需要注意这对自由匹配是否可以和另一对自由匹配交换匹配元素,形成一对自由匹配和一对限制匹配。也就是如果这次匹配了 \((a_i,b_j)\),则需要查看是否有 \((a_k,b_i)\) 或者 \((a_j,b_k)\) 这组匹配。如果有,那么可以叫互相交换匹配的一个元素让 \(cnt\) 加 \(1\)。
- 在上一点的前提下,交换了匹配后也有可能形成两对限制匹配,此时 \(cnt\) 应该加 \(2\) 而非加 \(1\)。
理清楚逻辑其实写起来十分简单。
时间复杂度 \(O(n\log n)\)。
代码
#include <bits/stdc++.h>
#define mp make_pair
#define st first
#define nd second
using namespace std;
typedef long long ll;
const int N=200010;
int Q,n,L,K,cnt,a[N],b[N],ma[N],mb[N];
ll ans;
priority_queue<pair<int,int> > qa,qb,qc,pa,pb;
int read()
{
int d=0; char ch=getchar();
while (!isdigit(ch)) ch=getchar();
while (isdigit(ch)) d=(d<<3)+(d<<1)+ch-48,ch=getchar();
return d;
}
void prework()
{
ans=0;
memset(ma,0,sizeof(ma));
memset(mb,0,sizeof(mb));
while (qa.size()) qa.pop();
while (qb.size()) qb.pop();
while (qc.size()) qc.pop();
while (pa.size()) pa.pop();
while (pb.size()) pb.pop();
}
void check(int i)
{
if (!ma[i] || !mb[i] || ma[i]==i) return;
if (ma[i]==mb[i]) cnt++;
mb[ma[i]]=mb[i]; ma[mb[i]]=ma[i];
ma[i]=mb[i]=i; cnt++;
}
void solve0()
{
while (ma[qa.top().nd]) qa.pop();
while (mb[qb.top().nd]) qb.pop();
int i=qa.top().nd,j=qb.top().nd;
qa.pop(); qb.pop();
ma[i]=j; mb[j]=i;
ans+=a[i]+b[j]; cnt-=(i!=j);
if (!mb[i]) pb.push(mp(b[i],i));
if (!ma[j]) pa.push(mp(a[j],j));
check(i); check(j);
}
int solve1()
{
while (qc.size() && (ma[qc.top().nd] || mb[qc.top().nd])) qc.pop();
if (qc.size()) return qc.top().st;
return -1;
}
int solve2()
{
while (qa.size() && ma[qa.top().nd]) qa.pop();
while (pb.size() && mb[pb.top().nd]) pb.pop();
if (qa.size() && pb.size())
return qa.top().st+pb.top().st;
return -1;
}
int solve3()
{
while (qb.size() && mb[qb.top().nd]) qb.pop();
while (pa.size() && ma[pa.top().nd]) pa.pop();
if (qb.size() && pa.size())
return qb.top().st+pa.top().st;
return -1;
}
void upd1()
{
int i=qc.top().nd; qc.pop();
ma[i]=mb[i]=i; ans+=a[i]+b[i];
}
void upd2()
{
int i=qa.top().nd,j=pb.top().nd,k=ma[j];
qa.pop(); pb.pop();
ma[j]=mb[j]=j; ma[i]=k; mb[k]=i;
cnt+=(i==k); ans+=b[j]+a[i];
if (!mb[i]) pb.push(mp(b[i],i));
check(i); check(k);
}
void upd3()
{
int i=qb.top().nd,j=pa.top().nd,k=mb[j];
qb.pop(); pa.pop();
ma[j]=mb[j]=j; mb[i]=k; ma[k]=i;
cnt+=(i==k); ans+=a[j]+b[i];
if (!ma[i]) pa.push(mp(a[i],i));
check(i); check(k);
}
int main()
{
Q=read();
while (Q--)
{
prework();
n=read(); K=read(); L=read();
for (int i=1;i<=n;i++) a[i]=read(),qa.push(mp(a[i],i));
for (int i=1;i<=n;i++) b[i]=read(),qb.push(mp(b[i],i));
for (int i=1;i<=n;i++) qc.push(mp(a[i]+b[i],i));
cnt=K-L;
while (K--)
{
if (cnt) { solve0(); continue; }
int v1=solve1(),v2=solve2(),v3=solve3();
if (v1>=max(v2,v3)) { upd1(); continue; }
if (v2>=max(v1,v3)) { upd2(); continue; }
if (v3>=max(v1,v2)) { upd3(); continue; }
}
cout<<ans<<"\n";
}
return 0;
}


