【CF1528B】Kavi on Pairing Duty

题目

题目链接：https://codeforces.com/problemset/problem/1528/B
有 \(2n\) 个点在一条直线上，你需要把他们两两配对（可以看作两两连线），一种配对方案是好的当且仅当不存在两条连线它们长度不一样且没有互相包含（也就是对于任意两条连线之间至少需要满足长度一样或者互相包含。
求好的配对方案数。
\(n\leq 10^6\)。

思路

记 \(f_i\) 表示 \(n=i\) 时的答案，考虑递推。
容易发现合法方案一定是拎出最左最右分别 \(k\) 个点，然后让这 \(2k\) 个点互相匹配（必须左边匹配右边），中间的点再互相匹配。这样才能满足如果长度不一就必须包含。
但是显然这样容易算重，比如下图

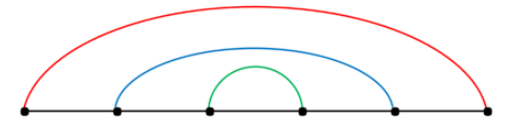
当 \(k=1\) 的时候被计算了一次，\(k=2\) 的时候也会计算一次。
所以我们要求枚举的左右 \(k\) 个互相匹配还需要满足匹配的路径两两交叉，这样每一种匹配方式对应了唯一一层去计算。
而 \(2k\) 个点两两交叉的匹配方式就只有一种（\(i\) 匹配 \(i+k\)），所以有

\[f_i=g_i+\sum^{i-1}_{j=1}f_j \]

其中 \(g_i\) 就表示不存在任何包含关系时，\(2i\) 个点的匹配方案数。
那么相当于要求所有匹配的线长度一致。假设 \(j\) 连向 \(j+k\)（或 \(j-k\)），那么一定有 \(k|i\)，不然无法恰好匹配。而不难发现对于任意 \(k|i\) 都有恰好一种匹配方式。所以 \(g_i\) 即为 \(i\) 的因子数量。
时间复杂度 \(O(n\log n)\)，采用线性筛可以做到 \(O(n)\)。

代码

#include <bits/stdc++.h>
using namespace std;

const int N=1000010,MOD=998244353;
int n,f[N],g[N];

int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
		for (int j=i;j<=n;j+=i)
			g[j]++;
	f[1]=1;
	for (int i=2;i<=n;i++)
		f[i]=(2*f[i-1]%MOD+g[i])%MOD;
	printf("%d",((f[n]-f[n-1])%MOD+MOD)%MOD);
	return 0;
}