【BZOJ#2119】股市的预测

题目

题目链接：https://darkbzoj.tk/problem/2119
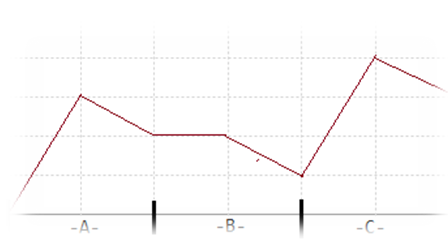
墨墨的妈妈热爱炒股，她要求墨墨为她编写一个软件，预测某只股票未来的走势。股票折线图是研究股票的必备工具，它通过一张时间与股票的价位的函数图像清晰地展示了股票的走势情况。经过长时间的观测，墨墨发现很多股票都有如下的规律：之前的走势很可能在短时间内重现！如图可以看到这只股票A部分的股价和C部分的股价的走势如出一辙。通过这个观测，墨墨认为他可能找到了一个预测股票未来走势的方法。进一步的研究可是难住了墨墨，他本想试图统计B部分的长度与发生这种情况的概率关系，不过由于数据量过于庞大，依赖人脑的力量难以完成，于是墨墨找到了善于编程的你，请你帮他找一找给定重现的间隔（B部分的长度），有多少个时间段满足首尾部分的走势完全相同呢？当然，首尾部分的长度不能为零。

题意简述：给定长度为 \(n\) 的数组 \(a\) 以及一个数字 \(m\)，将数组 \(a\) 作差分得到 \(a'\) 后，有多少子串 \([l,r]\) 满足 \(a[l\cdots r]=a[r+m+1\cdots r+m+1+(r-l)]\)。
\(n\leq 5\times 10^5,m\leq 10\)。

思路

既然是一个字符串内子串之间的匹配，考虑枚举子串长度 \(k\)，然后套路性把数组 \(k\) 倍数的位置标记，然后枚举所有标记位置前后统计答案。
具体的，枚举完长度 \(k\) 后，对于一个标记 \(i(k|i)\)，我们把所有长度为 \(k\)，且 \(l\leq i\leq r\) 的子串 \(a[l\cdots r]\) 在这次统计中计算贡献。
那么取 \(j=i+k+m\)，我们把 \(x=\text{LCS}(s[1\cdots i],s[1\cdots j])\) 和 \(y=\text{LCP}(s[i\cdots n],s[j\cdots n])\) 求出来，分别对 \(k\) 取 \(\min\)（因为我们要求必须经过 \(i\) 这个位置，所以长度不能超过 \(k\)），那么符合要求的子串数量就是 \(x+y-k\)。
那么就正反各建一个后缀数组就搞定了。时间复杂度 \(O(n\log n)\)。其实二分 + hash 也可以搞定的说

代码

封装后缀数组真香。

#include <bits/stdc++.h>
using namespace std;

const int N=50010,LG=16;
int n,m,tot,ans,a[N],b[N],lg[N];

struct SA
{
	int c[N],x[N],y[N],sa[N],rank[N],height[N],st[N][LG+1];
	
	void getsa(int *a)
	{
		int m=tot;
		for (int i=1;i<=n;i++) x[i]=a[i],c[x[i]]++;
		for (int i=1;i<=m;i++) c[i]+=c[i-1];
		for (int i=n;i>=1;i--) sa[c[x[i]]--]=i;
		for (int k=1;k<=n;k<<=1)
		{
			int num=0;
			for (int i=n-k+1;i<=n;i++) y[++num]=i;
			for (int i=1;i<=n;i++) if (sa[i]>k) y[++num]=sa[i]-k;
			for (int i=1;i<=m;i++) c[i]=0;
			for (int i=1;i<=n;i++) c[x[i]]++;
			for (int i=1;i<=m;i++) c[i]+=c[i-1];
			for (int i=n;i>=1;i--) sa[c[x[y[i]]]--]=y[i],y[i]=0;
			swap(x,y);
			x[sa[1]]=num=1;
			for (int i=2;i<=n;i++)
				x[sa[i]]=(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num : ++num;
			if (m==num) break;
			m=num;
		}
	}
	
	void geth(int *a)
	{
		for (int i=1;i<=n;i++) rank[sa[i]]=i;
		for (int i=1,k=0;i<=n;i++)
		{
			if (k) k--;
			int j=sa[rank[i]-1];
			while (a[i+k]==a[j+k]) k++;
			height[rank[i]]=k;
		}
	}
	
	void buildst()
	{
		for (int i=1;i<=n;i++) st[i][0]=height[i];
		for (int i=n;i>=1;i--)
			for (int j=1;i+(1<<j)-1<=n;j++)
				st[i][j]=min(st[i][j-1],st[i+(1<<j-1)][j-1]);
	}
	
	int lcp(int i,int j)
	{
		i=rank[i]; j=rank[j];
		if (i>j) swap(i,j);
		int k=lg[j-i];
		return min(st[i+1][k],st[j-(1<<k)+1][k]);
	}
	
	void work(int *a) { getsa(a); geth(a); buildst(); }
}sa[2];

int main()
{
	scanf("%d%d",&n,&m);
	for (int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
	for (int i=1;i<=n;i++) scanf("%d",&a[i]);
	for (int i=n;i>=1;i--) a[i]-=a[i-1];
	for (int i=1;i<=n;i++) a[i]=b[i]=a[i+1];
	n--;
	sort(b+1,b+1+n);
	tot=unique(b+1,b+1+n)-b-1;
	for (int i=1;i<=n;i++)
		a[i]=lower_bound(b+1,b+1+tot,a[i])-b;
	for (int i=1;i<=n;i++) b[i]=a[n-i+1];
	sa[0].work(a); sa[1].work(b);
	for (int i=1;i<=n;i++)
		for (int j=i;j+m+i<=n;j+=i)
		{
			int x=min(sa[0].lcp(j,j+m+i),i),y=min(sa[1].lcp(n-j+1,n-j-m-i+1),i);
			ans+=max(x+y-i,0);
		}
	printf("%d\n",ans);
	return 0;
}