【YbtOJ#573】后缀表达

题目

题目链接：https://www.ybtoj.com.cn/contest/115/problem/2



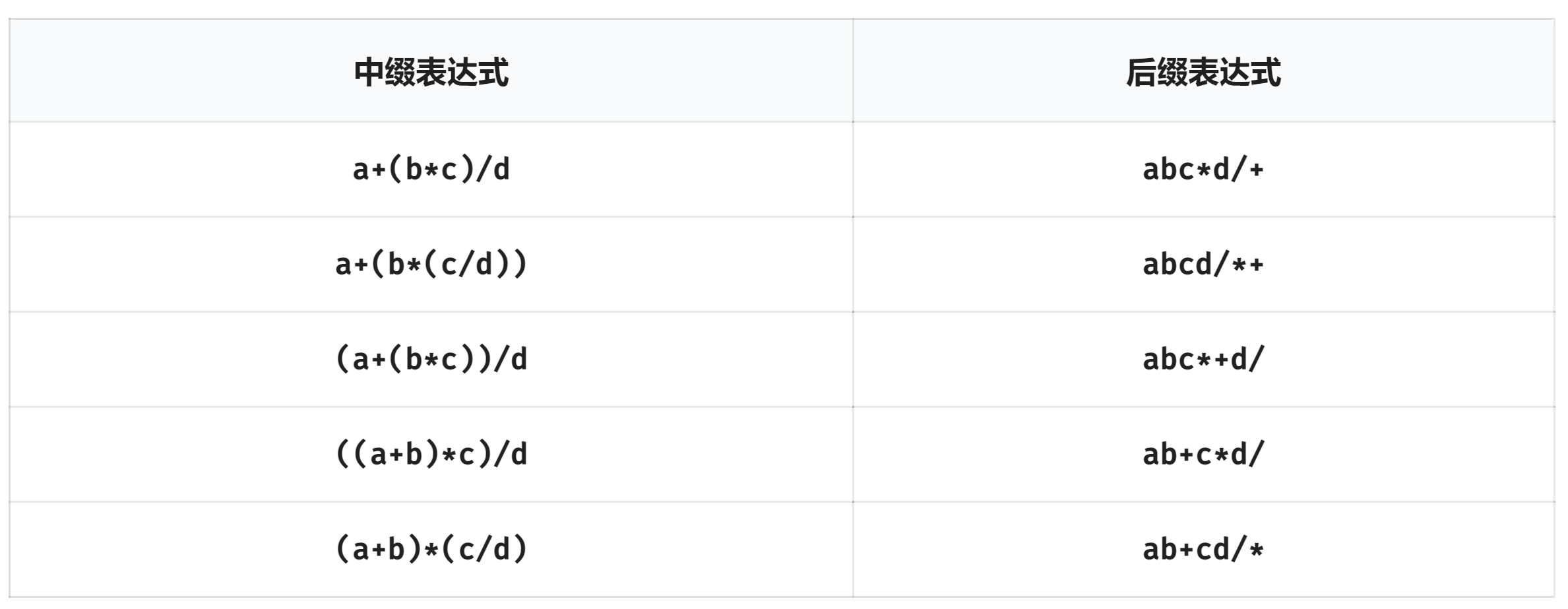
\(n\leq 2500\)。

思路

建出表达式树，如果一个非叶子节点有多个相同字母儿子显然可以把相同字母合并。
然后由于满足结合律，如果一个符号存在一个相同符号儿子，那么就可以把这个儿子的所有儿子合并到上面。注意字母重复依然要合并。
然后考虑在树上 dp。
设 \(f_x\) 表示节点 \(x\) 的子树合并后最少占用单元。
如果直接把所有儿子连起来，那么

\[f_x=1+\sum_{y\in \text{son}(x)}f_y \]

因为我们把所有字母合并了，现在可能减小占用单元当且仅当一个叶子节点排在一个非叶子节点前面，并且这个非叶子节点存在一种排序使得叶子节点所表示字母可以排在最前面的同时，所需单元不增加。因为如果所需单元增加，而我们只能减小 \(1\) 个单元，所以显然不优。
由于一个叶子只能和一个非叶子结合，考虑二分图匹配。左边是 \(26\) 个字母，右边是儿子节点。记 \(avl[x][i]\) 表示节点 \(x\) 能否在不增加最少需要单元的前提下把字母 \(i\) 移到最前面，那么如果 \(avl[v][i]=1\)，就从 \(i\) 向 \(v\) 连边。然后最大匹配就是最多能减小的单元。
接下来考虑如何合并 \(avl[x]\)。\(avl[x][i]=1\) 当且仅当 \(x\) 有 \(i\) 字母这个儿子；或者存在儿子 \(v\) 满足 \(avl[v][i]=1\) 并且最大匹配可以不匹配 \(v\)。
那么如果本来就没有匹配显然可行，如果本来匹配了，我们就从它的匹配点再尝试找一条增广路，如果找得到那么说明可以不用匹配 \(v\)。
答案就是 \(f[n]\)。
时间复杂度 \(O(mn^2)\)，其中 \(m=26\)。

代码

#include <bits/stdc++.h>
using namespace std;

const int N=1000050;
int n;
char s[N];

struct edge
{
	int next,to;
	bool del;
};

struct Graph
{
	int tot,head[N],vis[N],pos[N];
	edge e[N];
	
	void clr(int k)
	{
		for (int i=N-1;i>=N-30;i--)
			pos[i]=0,vis[i]=0,head[i]=-1;
		for (int i=0;i<=k;i++)
			pos[i]=0,vis[i]=0,head[i]=-1;
		tot=0;
	}
	
	void add(int from,int to)
	{
		e[++tot]=(edge){head[from],to,0};
		head[from]=tot;
	}
	
	bool dfs(int x,int t)
	{
		if (vis[x]==t) return 0;
		vis[x]=t;
		for (int i=head[x];~i;i=e[i].next)
		{
			int v=e[i].to;
			if (!pos[v] || dfs(pos[v],t))
			{
				pos[v]=x;
				return 1;
			}
		}
		return 0;
	}
	
	bool find(int i)
	{
		if (!pos[i]) return 1;
		return dfs(pos[i],i+19260817);
	}
}G;

struct Tree
{
	int tot,head[N],f[N],rk[N];
	bool typ[N][30],avl[N][30];
	edge e[N];
	
	void add(int from,int to)
	{
		if (s[to]>='a' && s[to]<='z')
		{
			if (typ[from][s[to]-'a']) return;
			typ[from][s[to]-'a']=1;
		}
		e[++tot]=(edge){head[from],to,0};
		head[from]=tot;
	}
	
	void dfs1(int x)
	{
		for (int i=head[x];~i;i=e[i].next)
		{
			int v=e[i].to;
			dfs1(v);
			if (s[v]==s[x])
			{
				for (int j=head[v];~j;j=e[j].next)
					if (!e[j].del) add(x,e[j].to),e[j].del=1;
				e[i].del=1;
			}
		}
	}
	
	void dfs2(int x)
	{
		f[x]=1;
		if (head[x]==-1) return;
		for (int i=head[x];~i;i=e[i].next)
		{
			int v=e[i].to;
			if (!e[i].del) dfs2(v);
		}
		tot=0;
		for (int i=head[x];~i;i=e[i].next)
			if (!e[i].del)
			{
				int v=e[i].to;
				f[x]+=f[v]; rk[++tot]=v;
				for (int j=0;j<26;j++)
					if (typ[x][j] && avl[v][j])
						G.add(N-1-j,tot);
			}
		for (int i=0;i<26;i++)
			if (typ[x][i] && G.dfs(N-1-i,i+1)) f[x]--;
		for (int i=1;i<=tot;i++)
			if (G.find(i))
				for (int j=0;j<26;j++)
					avl[x][j]|=avl[rk[i]][j];
		G.clr(tot);
		for (int i=0;i<26;i++)
			avl[x][i]|=typ[x][i];
	}
}T;

void build()
{
	stack<int> st;
	for (int i=1;i<=n;i++)
	{
		if (s[i]<'a' || s[i]>'z')
		{
			int x=st.top(); st.pop();
			int y=st.top(); st.pop();
			T.add(i,x); T.add(i,y);
		}
		st.push(i);
	}
}

int main()
{
	freopen("expr.in","r",stdin);
	freopen("expr.out","w",stdout);
	memset(T.head,-1,sizeof(T.head));
	memset(G.head,-1,sizeof(G.head));
	scanf("%s",s+1);
	n=strlen(s+1);
	build();
	T.dfs1(n); T.dfs2(n);
	printf("%d",T.f[n]);
	return 0;
}