【洛谷P5055】【模板】可持久化文艺平衡树

题目

题目链接：https://www.luogu.com.cn/problem/P5055
您需要写一种数据结构，来维护一个序列，其中需要提供以下操作（对于各个以往的历史版本）：

1. 在第 \(p\) 个数后插入数 \(x\) 。
2. 删除第 \(p\) 个数。
3. 翻转区间 \([l,r]\)，例如原序列是 \(\{5,4,3,2,1\}\)，翻转区间 \([2,4]\) 后，结果是 \(\{5,2,3,4,1\}\)。
4. 查询区间 \([l,r]\) 中所有数的和。

和原本平衡树不同的一点是，每一次的任何操作都是基于某一个历史版本，同时生成一个新的版本（操作 \(4\) 即保持原版本无变化），新版本即编号为此次操作的序号。
本题强制在线。
\(n\leq 2\times 10^5,|x|\leq 10^6\)。

思路

FTQ Treap 维护区间操作十分简单：直接把前 \(r\) split 出来，再把前 \(l-1\) 规范 split 出来，就得到 \([l,r]\) 了。
所以我们可以像 Splay 一样进行区间翻转，维护区间和。
但是注意除了在 split 和 merge 处要复制节点以外，在 pushdown 处也要复制节点。因为可能出现下图的情况

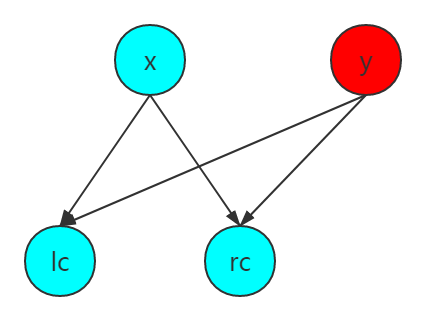
其中 \(y\) 是 \(x\) 复制过来的节点，假设 \(y\) 有翻转标记且此时我们 pushdown \(y\)，那么就会把 \(x\) 的儿子给翻转。下次询问 \(x\) 的信息时就会出错。
所以为了方便 pushdown，FHQ Treap 一个节点的翻转标记表示这个点的两个儿子还没有被翻转。也就是 pushdown \(x\) 时需要翻转 \(x\) 的左右儿子，同时下传标记。
空间往大的开就行了。
时间复杂度 \(O(n\log n)\)。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N=200010,MAXN=N*100;
int n,rt[N];
ll last;

struct FHQ
{
	int tot,ch[MAXN][2],val[MAXN],dat[MAXN],siz[MAXN];
	ll sum[MAXN];
	bool rev[MAXN];
	
	int cpynode(int x)
	{
		int y=++tot;
		ch[y][0]=ch[x][0]; ch[y][1]=ch[x][1];
		val[y]=val[x]; dat[y]=dat[x]; siz[y]=siz[x];
		sum[y]=sum[x]; rev[y]=rev[x];
		return y;
	}
	
	void pushup(int x)
	{
		siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+1;
		sum[x]=sum[ch[x][0]]+sum[ch[x][1]]+val[x];
	}
	
	void pushdown(int x)
	{
		if (rev[x])
		{
			if (ch[x][0]) ch[x][0]=cpynode(ch[x][0]);
			if (ch[x][1]) ch[x][1]=cpynode(ch[x][1]);
			swap(ch[x][0],ch[x][1]);
			rev[ch[x][0]]^=1; rev[ch[x][1]]^=1; rev[x]=0;
		}
	}
	
	int New(int v)
	{
		int x=++tot;
		val[x]=sum[x]=v; dat[x]=rand(); siz[x]=1;
		return x;
	}
	
	void split(int x,int k,int &lc,int &rc)
	{
		if (!x) { lc=rc=0; return; }
		pushdown(x);
		int y=cpynode(x);
		if (siz[ch[y][0]]>=k)
			rc=y,split(ch[y][0],k,lc,ch[y][0]);
		else
			lc=y,split(ch[y][1],k-siz[ch[x][0]]-1,ch[y][1],rc);
		pushup(y);
	}
	
	int merge(int x,int y)
	{
		if (!x || !y) return x|y;
		pushdown(x); pushdown(y);
		if (dat[x]>dat[y])
		{
			int z=cpynode(x);
			ch[z][1]=merge(ch[z][1],y);
			pushup(z); return z;
		}
		else
		{
			int z=cpynode(y);
			ch[z][0]=merge(x,ch[z][0]);
			pushup(z); return z;
		}
	}
	
	void ins(int &root,int k,int v)
	{
		int x,y;
		split(root,k,x,y);
		root=merge(merge(x,New(v)),y);
	}
	
	void del(int &root,int k)
	{
		int x,y,z;
		split(root,k,x,y); split(x,k-1,x,z);
		root=merge(x,y);
	}
	
	void reverse(int &root,int l,int r)
	{
		int x,y,z;
		split(root,r,x,y); split(x,l-1,z,x);
		rev[x]^=1;
		root=merge(merge(z,x),y);
	}
	
	ll query(int &root,int l,int r)
	{
		int x,y,z;
		split(root,r,x,y); split(x,l-1,z,x);
		ll ans=sum[x];
		root=merge(merge(z,x),y);
		return ans;
	}
}fhq;

int main()
{
	srand(1023);
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	{
		int opt,now; ll x,y;
		scanf("%d%d",&now,&opt);
		scanf("%lld",&x);
		if (opt!=2) scanf("%lld",&y);
		rt[i]=rt[now]; x^=last; y^=last;
		if (opt==1) fhq.ins(rt[i],x,y);
		if (opt==2) fhq.del(rt[i],x);
		if (opt==3) fhq.reverse(rt[i],x,y);
		if (opt==4) printf("%lld\n",last=fhq.query(rt[i],x,y));
	}
	return 0;
}