【洛谷P2668】斗地主

题目

题目链接：https://www.luogu.com.cn/problem/P2668
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的\(A\)到\(K\)加上大小王的共\(54\)张牌来进行的扑克牌游戏。在斗地主中，牌的大小关 系根据牌的数码表示如下：\(3<4<5<6<7<8<9<10<J<Q<K<A<2<\text{小王}<\text{大王}\)，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由 \(n\) 张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下：

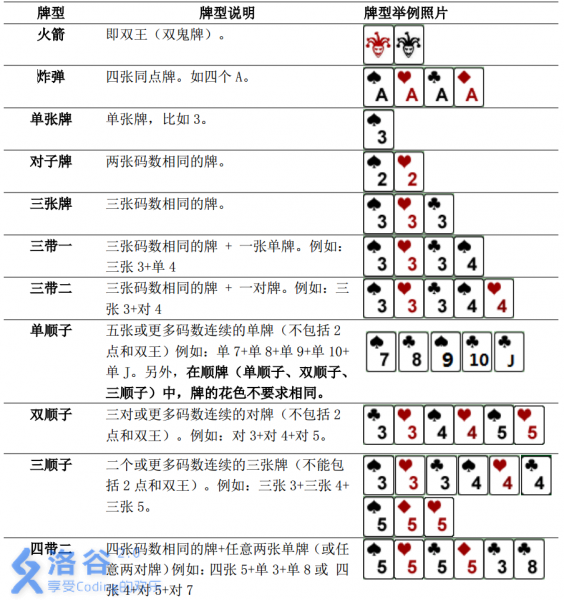
思路

此代码也可以 AC P2540 斗地主增强版
今年 CSP 考了一道模拟，不知道 NOIp 会不会考一些奇奇怪怪的题，所以就随便找了一道 NOIp 历年的搜索来写。
这道题思路很简单，就是直接按顺子，带牌，单牌来搜。加上一点小剪枝就可以了。
注意到了出单牌的时候就不要用递归去搜了，直接 for 一遍就可以了。否则会 T。

代码

#include <bits/stdc++.h>
using namespace std;

const int QAyyds[4]={0,4,2,1};
int Q,n,ans,a[20]; 

int mincnt(int l,int r)
{
	int minn=2e9;
	for (int i=l;i<=r;i++)
		minn=min(minn,a[i]);
	return minn;
}

void dfs(int n,int cnt,int f1,int f2,int f3)
{
	if (cnt>=ans) return;
	if (!n)
	{
		ans=cnt;
		return;
	}
	// 顺子 
	if (f1!=-1)
		for (int k=f1;k<=3;k++)
			for (int i=3;i<=14;i++)
				for (int j=i+QAyyds[k];j<=14;j++)
					if (mincnt(i,j)>=k)
					{
						for (int l=i;l<=j;l++) a[l]-=k;
						dfs(n-(j-i+1)*k,cnt+1,k,f2,f3);
						for (int l=i;l<=j;l++) a[l]+=k;
					}
					else break;
	// 四带
	if (f2!=-1)
		for (int i=f2;i<=14;i++)
			if (a[i]>=4)
			{
				a[i]-=4;
				for (int j=2;j<=14;j++)
					if (a[j]>=2)
					{
						a[j]-=2;
						for (int k=j;k<=14;k++)
							if (a[k]>=2) { a[k]-=2; dfs(n-8,cnt+1,-1,i+1,f3); a[k]+=2; }
						a[j]+=2;
					}
				for (int j=0;j<=14;j++)
					if (a[j])
					{
						a[j]--;
						for (int k=j;k<=14;k++)
							if (a[k]) { a[k]--; dfs(n-6,cnt+1,-1,i+1,f3); a[k]++; }
						a[j]++;
					}
				a[i]+=4;
			}
	// 三带
	if (f3!=-1)
		for (int i=f3;i<=14;i++)
			if (a[i]>=3)
			{
				a[i]-=3;
				for (int j=2;j<=14;j++)
					if (a[j]>=2) { a[j]-=2; dfs(n-5,cnt+1,-1,-1,i+1); a[j]+=2; }
				for (int j=0;j<=14;j++)
					if (a[j]) { a[j]--; dfs(n-4,cnt+1,-1,-1,i+1); a[j]++; }
				a[i]+=3;
			}
	for (int i=0;i<=14;i++)
		if (a[i]) cnt++;
	if (a[0] && a[1]) cnt--;
	ans=min(ans,cnt);
	if (a[0] && a[1]) cnt++;
	for (int i=0;i<=14;i++)
		if (a[i]) cnt--;
}

int main()
{
	scanf("%d%d",&Q,&n);
	while (Q--)
	{
		ans=2e9;
		memset(a,0,sizeof(a));
		for (int i=1,x,y;i<=n;i++)
		{
			scanf("%d%d",&x,&y);
			if (!x) a[x+y-1]++;
			else if (x==1) a[14]++;
			else a[x]++;
		}
		dfs(n,0,1,2,2);
		printf("%d\n",ans);
	}
	return 0;
}