【洛谷P1117】优秀的拆分
题目
题目链接:https://www.luogu.com.cn/problem/P1117
如果一个字符串可以被拆分为 \(\text{AABB}\) 的形式,其中 \(\text{A}\) 和 \(\text{B}\) 是任意非空字符串,则我们称该字符串的这种拆分是优秀的。
例如,对于字符串 $ \texttt{aabaabaa} $ ,如果令 \(\text{A}=\texttt{aab}\),\(\text{B}=\texttt{a}\),我们就找到了这个字符串拆分成 \(\text{AABB}\) 的一种方式。
一个字符串可能没有优秀的拆分,也可能存在不止一种优秀的拆分。
比如我们令 \(\text{A}=\texttt{a}\),\(\text{B}=\texttt{baa}\),也可以用 \(\text{AABB}\) 表示出上述字符串;但是,字符串 \(\texttt{abaabaa}\) 就没有优秀的拆分。
现在给出一个长度为 \(n\) 的字符串 \(S\),我们需要求出,在它所有子串的所有拆分方式中,优秀拆分的总个数。这里的子串是指字符串中连续的一段。
以下事项需要注意:
- 出现在不同位置的相同子串,我们认为是不同的子串,它们的优秀拆分均会被记入答案。
- 在一个拆分中,允许出现 \(\text{A}=\text{B}\)。例如 \(\texttt{cccc}\) 存在拆分 \(\text{A}=\text{B}=\texttt{c}\)。
- 字符串本身也是它的一个子串。
思路
设 \(f[i]\) 表示以位置 \(i\) 开头的形如 AA 的字符串的数量,\(g[i]\) 表示以位置 \(i\) 结尾的形如 AA 的字符串数量。显然答案为 \(\sum^{n}_{i=1}g[i-1]f[i]\)。
枚举形如 AA 的字符串中其中一半的长度 \(k\)。在原串上每 \(k\) 个位置设立一个关键点,那么显然任意一个长度为 \(2k\) 的形如 AA 的字符串都一定经过两个关键点。
考虑相邻的两个关键点 \(i,j(j=i+k)\) 会产生的贡献。我们求出以 \(i\) 和 \(j\) 开头的两个后缀的 LCP,长度计为 \(l1\),再求出以 \(i-1\) 和 \(j-1\) 结尾的两个前缀的 LCS,长度计为 \(l2\)。
那么可以得到下图的信息:
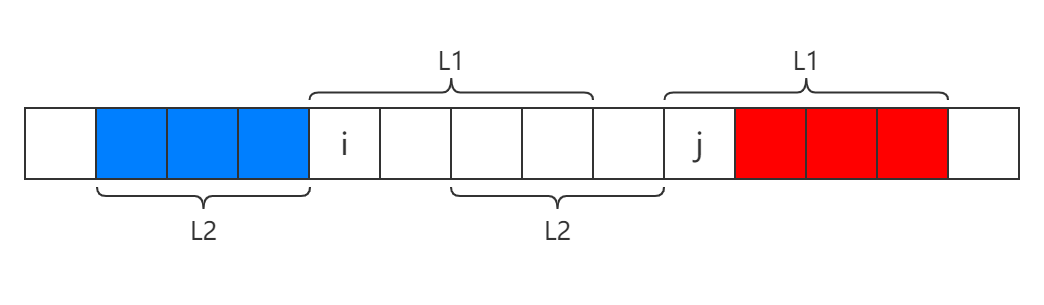
显然如果 \(l1+l2<k\),那么无论如何不可能存在一个形如 AA 的长度为 \(k\) 的子串经过 \(i,j\)。否则一定存在 \(l1+l2-k+1\) 个这样的子串。例如上图中蓝色部分就是长度为 \(2\times 5\) 的开始位置,红色部分就是长度为 \(2\times 5\) 的结束位置。
我们可以通过这些信息计算出蓝色部分和红色部分,然后用差分来求出 \(f\) 和 \(g\) 即可。
时间复杂度 \(O(n\log n)\)。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=30010,LG=15;
int Q,n,m,x[N],y[N],c[N],f[N],g[N],lg[N],sa[2][N],rk[2][N],height[2][N],rmq[2][N][LG+1];
char s[N],t[N];
ll ans;
int Quant,Ask,my,dog;
void SA(char *s,int *sa)
{
for (int i=1;i<=m;i++) c[i]=0;
for (int i=1;i<=n;i++) x[i]=s[i],c[x[i]]++;
for (int i=2;i<=m;i++) c[i]+=c[i-1];
for (int i=n;i>=1;i--) sa[c[x[i]]--]=i;
for (int k=1;k<=n;k<<=1)
{
int num=0;
for (int i=n-k+1;i<=n;i++) y[++num]=i;
for (int i=1;i<=n;i++) if (sa[i]>k) y[++num]=sa[i]-k;
for (int i=1;i<=m;i++) c[i]=0;
for (int i=1;i<=n;i++) c[x[i]]++;
for (int i=2;i<=m;i++) c[i]+=c[i-1];
for (int i=n;i>=1;i--) sa[c[x[y[i]]]--]=y[i],y[i]=0;
swap(x,y);
x[sa[1]]=num=1;
for (int i=2;i<=n;i++)
x[sa[i]]=(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num : ++num;
m=num;
if (n==m) break;
}
}
void geth(char *s,int id)
{
for (int i=1;i<=n;i++) rk[id][sa[id][i]]=i;
for (int i=1,k=0;i<=n;i++)
{
if (k) k--;
int j=sa[id][rk[id][i]-1];
while (s[i+k]==s[j+k]) k++;
height[id][rk[id][i]]=k;
}
}
void getst(int id)
{
for (int i=1;i<=n;i++) rmq[id][i][0]=height[id][i];
for (int j=1;j<=LG;j++)
for (int i=1;i+(1<<j)-1<=n;i++)
rmq[id][i][j]=min(rmq[id][i][j-1],rmq[id][i+(1<<(j-1))][j-1]);
}
int LCP(int id,int i,int j)
{
i=rk[id][i]; j=rk[id][j];
if (i>j) swap(i,j);
int t=lg[j-i];
return min(rmq[id][i+1][t],rmq[id][j-(1<<t)+1][t]);
}
void prework()
{
memset(f,0,sizeof(f));
memset(g,0,sizeof(g));
memset(x,0,sizeof(x));
memset(y,0,sizeof(y));
memset(c,0,sizeof(c));
memset(sa,0,sizeof(sa));
memset(rk,0,sizeof(rk));
memset(height,0,sizeof(height));
memset(rmq,0,sizeof(rmq));
ans=0;
}
int main()
{
lg[1]=0;
for (int i=2;i<N;i++)
lg[i]=lg[i>>1]+1;
scanf("%d",&Q);
while (Q--)
{
prework();
scanf("%s",s+1);
n=strlen(s+1); m='z'+1;
for (int i=1;i<=n;i++)
t[i]=s[n-i+1];
SA(s,sa[0]); geth(s,0); getst(0);
SA(t,sa[1]); geth(t,1); getst(1);
for (int k=1;k<=n;k++)
for (int i=k;i+k<=n;i+=k)
{
int j=i+k,l1=min(LCP(0,i,j),k),l2=min(LCP(1,n-(i-1)+1,n-(j-1)+1),k-1);
if (l1+l2<k) continue;
int len=l2+l1-k+1;
f[i-l2]++; f[i-l2+len]--;
g[j+l1-len]++; g[j+l1]--;
}
for (int i=1;i<=n;i++)
{
f[i]+=f[i-1]; g[i]+=g[i-1];
ans+=g[i-1]*f[i];
}
printf("%lld\n",ans);
}
return 0;
}


