【洛谷P6772】美食家

题目

题目链接：https://www.luogu.com.cn/problem/P6772
坐落在 Bzeroth 大陆上的精灵王国击退地灾军团的入侵后，经过十余年的休养生息，重新成为了一片欣欣向荣的乐土，吸引着八方游客。小 W 是一位游历过世界各地的著名美食家，现在也慕名来到了精灵王国。

精灵王国共有 \(n\) 座城市，城市从 \(1\) 到 \(n\) 编号，其中城市 \(i\) 的美食能为小 W 提供 \(c_i\) 的愉悦值。精灵王国的城市通过 \(m\) 条单向道路连接，道路从 \(1\) 到 \(m\) 编号，其中道路 \(i\) 的起点为城市 \(u_i\) ，终点为城市 \(vi_\)，沿它通行需要花费 \(w_i\) 天。也就是说，若小 W 在第 \(d\) 天从城市 \(u_i\) 沿道路 \(i\) 通行，那么他会在第 \(d + w_i\) 天到达城市 \(v_i\)。

小 W 计划在精灵王国进行一场为期 \(T\) 天的旅行，更具体地：他会在第 \(0\) 天从城市 \(1\) 出发，经过 \(T\) 天的旅行，最终在恰好第 \(T\) 天回到城市 \(1\) 结束旅行。由于小 W 是一位美食家，每当他到达一座城市时（包括第 \(0\) 天和第 \(T\) 天的城市 \(1\)），他都会品尝该城市的美食并获得其所提供的愉悦值，若小 W 多次到达同一座城市，他将获得多次愉悦值。注意旅行途中小 W 不能在任何城市停留，即当他到达一座城市且还未结束旅行时，他当天必须立即从该城市出发前往其他城市。

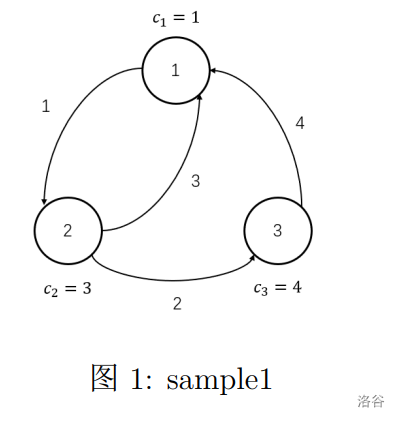
对于上图，小 W 一种为期 \(11\) 天的可行旅游方案为 \(1 \to 2 \to 1 \to 2 \to 3 \to 1\)：

• 第 \(0\) 天，小 W 从城市 \(1\) 开始旅行，获得愉悦值 \(1\) 并向城市 \(2\) 出发。
• 第 \(1\) 天，小 W 到达城市 \(2\)，获得愉悦值 \(3\) 并向城市 \(1\) 出发。
• 第 \(4\) 天，小 W 到达城市 \(1\)，获得愉悦值 \(1\) 并向城市 \(2\) 出发。
• 第 \(5\) 天，小 W 到达城市 \(2\)，获得愉悦值 \(3\) 并向城市 \(3\) 出发。
• 第 \(7\) 天，小 W 到达城市 \(3\)，获得愉悦值 \(4\) 并向城市 \(1\) 出发。
• 第 \(11\) 天，小 W 到达城市 \(1\)，获得愉悦值 \(1\) 并结束旅行。
• 小 W 在该旅行中获得的愉悦值之和为 \(13\)。

此外，精灵王国会在不同的时间举办 \(k\) 次美食节。具体来说，第 \(i\) 次美食节将于第 \(t_i\) 天在城市 \(x_i\) 举办，若小 W 第 \(t_i\) 天时恰好在城市 \(x_i\)，那么他在品尝城市 \(x_i\) 的美食时会额外得到 \(y_i\) 的愉悦值。现在小 W 想请作为精灵王国接待使者的你帮他算出，他在旅行中能获得的愉悦值之和的最大值。

思路

首先如果没有美食节和路径长度，那么这道题就是裸的矩阵乘法。
我们发现这道题的边权不超过 \(5\)，所以考虑将每条边拆成 \(5\) 条边来跑，这样还是相当于边权为 \(1\)，但是点的数量为 \(5n\leq 250\)。
此时如果没有美食节，那么仍然直接矩阵乘法即可。
加入了美食节后，显然要在每两个美食节中间用矩阵快速幂计算出这几天的答案，然后加上美食节贡献。
但是直接这样做是 \(O(kn^3\log t)\) 的，不可接受。
发现每次都要计算两次美食节之间的代价大量运算重复，所以可以先预处理出矩阵的 \(2^i\) 幂，然后每次 \(O(\log t)\) 倍增求出。
然后答案是一个 \(1\times n\) 的矩阵，向量乘矩阵的复杂度是 \(O(n^2)\) 的，这样时间复杂度就被我们降到了 \(O(kn^2\log t)\)。
总时间复杂度 \(O(n^3\log t+kn^2\log t)\)。此处 \(n\) 等于原题中 \(5n\)。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N=260,LG=30;
int n,m,t,k,tot,maxn,a[N];

int ID(int x,int y)
{
	return y*n+x;
}

struct node
{
	int t,x,a;
}b[N];

bool cmp(node x,node y)
{
	return x.t<y.t;
}

struct Matrix
{
	ll a[N][N];
	Matrix() { memset(a,0xcf,sizeof(a)); }
	
	friend Matrix operator *(const Matrix &a,const Matrix &b)
	{
		Matrix c;
		for (int i=1;i<=maxn;i++)
			for (int j=1;j<=tot;j++)
				for (int k=1;k<=tot;k++)
					c.a[i][j]=max(c.a[i][j],a.a[i][k]+b.a[k][j]);
		return c;
	}
}ans,f[LG+1];

Matrix fpow(Matrix a,int k)
{
	for (int i=LG;i>=0;i--)
		if (k&(1<<i)) a=a*f[i];
	return a;
}

int main()
{
	scanf("%d%d%d%d",&n,&m,&t,&k);
	for (int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		for (int j=0;j<4;j++)
			f[0].a[ID(i,j)][ID(i,j+1)]=0;
	}
	tot=5*n;
	for (int i=1,x,y,z;i<=m;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		f[0].a[ID(x,z-1)][y]=a[y];
	}
	maxn=tot;
	for (int i=1;i<=LG;i++)
		f[i]=f[i-1]*f[i-1];
	maxn=1;
	for (int i=1;i<=k;i++)
		scanf("%d%d%d",&b[i].t,&b[i].x,&b[i].a);
	sort(b+1,b+1+k,cmp);
	b[k+1].t=t;
	ans.a[1][1]=a[1];
	ans=fpow(ans,b[1].t);
	for (int i=1;i<=k;i++)
	{
		ans.a[1][b[i].x]+=b[i].a;
		ans=fpow(ans,b[i+1].t-b[i].t);
	}
	ll WYCtxdy=ans.a[1][1];
	if (WYCtxdy<0) printf("-1");
		else printf("%lld",WYCtxdy);
	return 0;
}