1、判断一个单链表中是否有环
思路:给定两个指针fast和low都指向头结点,然后low每次前进一步,fast每次前进两步,如果此单链表中有环,那么fast和low一定会相遇,否则fast一定会先遇到null。实现代码如下:
bool isCircle(LinkList *head)
{
LinkList *fast = head;//快指针
LinkList *low = head;//慢指针
while(low->next != NULL && fast->next->next != NULL)
{
low = low->next;
fast = fast->next->next;
if (low == fast)
{
return true;
}
}
return false;
}
现在还有个问题需要思考,为什么如果链表有环,fast和low就一定会相遇呢?
假设单链表长度为n,且该单链表是环状的。
① 若low和fast的起点相同,那么第i次迭代时,low指向元素(i mod n),q指向(2i mod n)。因此当i≡2i(mod n)时,fast和low相遇。而i≡2i(mod n) → (2i-i)mod n=0 → (i mod n) = 0 →当i=n时,fast和low相遇。
② 若low和fast的起点不同,假设第i次迭代时low指向元素(i mod n),fast指向((k+2i) mod n),其中0<k<n。那么i≡(2i+k) mod n → (i+k) mod n =0 →当i=n-k时,fast和low相遇。
由上面的题目可以引申出下面的题目:
(1)如果两个之争的速度不一样,比如p和q(0<p<q)二者满足什么样的关系,可以使得两者肯定交与一个节点?
Sp(i) = pi
Sq(i) = k + qi
如果两个要相交于一个节点,则Sp(i)=Sq(i) → (pi) mod n = ( k+ qi ) mod n → [(q-p)i + k] mod n =0 → (q-p)i + k = Nn [N 为自然数] → i=(Nn-k) /(p-q)
i取自然数,则当p,q满足上面等式,即存在一个自然数N使得(Nn-k)是(p-q)的倍数时,保证两者相交。
特例:如果q 是p 的步长的两倍,都从同一个起点开始,即 q=2p , k=0, 那么等式变为: Nn=i。 即可以理解为,当第i次迭代时,i是圈的整数倍时,两者相交,交点就是为起点。
(2)如何判断单链表的环的长度?
这个问题比较简单,知道q已经进入到环中,保存该位置,然后由该位置遍历,当再次碰到该q位置时所迭代的次数就是环的长度。
(3)如何找到单链表中环的入口节点?
假设链表长度是L,前半部分长度为k-1,那么第一个在环里的节点是k,环的长度是 n, 那么当q=2p时, 什么时候第一次相交呢?当q指针走到第k个节点时,q指针已经在环的第 k mod n 的位置。即p和q相差k个元素,从不同的起点开始,则相交的位置为 n-k, 则有了下面的图:
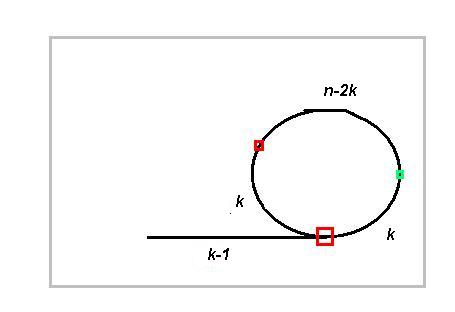
从图上可以明显看到,当p从交点的位置(n-k) ,向前遍历k个节点就到到达环的第一个几点,节点k.
算法就很简单: 一个指针从p和q 中的第一次相交的位置起(n-k),另外一个指针从链表头开始遍历,其交点就是链表中第一个在环里的交点。
(4)给定两个单链表(head1,head2),判断两个链表是否有交点,如果有,第一个交点在哪里?
这个问题很容易转化为前面的题目。

将其中一个链表中的尾节点与头节点联系起来,则很容发现问题转化为问题3,求有环的链表的第一个在环里的节点。
2、给定单链表头结点,删除链表中倒数第k个结点。
使用两个节点low和fast,low初始化指向头结点,fast一直指向low后的第k个节点,两个结点平行向后移动,直到fast到达链表尾部(NULL)时,删除low所对应的结点。
3、单链表的反转
这是个经常考但是也很基础的题目。实现代码如下:
struct node
{
int data;
struct node *next;
};
typedef struct node ListNode;
typedef ListNode *LinkNode;
LinkNode reverse(LinkNode head)
{
LinkNode p1,p2,p3;
//如果没有结点或只有头结点
if(head == NULL || head->next == NULL)
return head;
p1 = head;
p2 = head->next;
head->next = NULL;//反转后head成为最后一个结点
//链表中有大于一个结点
while(p1->next != NULL)
{
p3 = p2->next;
p2->next = p1;
p1 = p2;
p2 = p3;
}
head = p1;
return head;
}



