暑假 D4T2 rabbit(割点 矿场搭建)
Description
众所周知,Bfk家的后院有一片胡萝卜田
这片田地很受兔子们的喜爱,兔子们为了方便偷吃胡萝卜,在地下打出了一片洞穴网络。Bfk早就发现了它家的萝卜田里兔子泛滥的情形,因此,它决定先外出旅游几天,让兔子们放松警惕,回家时再将兔子们一网打尽。
具体的,我们可以将洞穴网络抽象成一个n条边的图。bfk的策略是,随机堵住某个节点,如果这个点是地下网络的必经之路,那么它就可以守洞待兔了。兔子们并不想坐以待毙,因此它们决定在某些节点挖出通向地面的出口,使得无论bfk堵住哪个节点,兔子们都可以直接从某个出口溜走。
但是兔子们只会计算1+1=2,对于如此复杂的问题,它们毫无头绪。请你帮忙计算一下,兔子们至少需要挖多少个出口才能满足上述条件,以及在出口数最少的情况下,出口的分布方式有多少种
Input
第一行一个正整数n,表示地下网络的边数
接下来n行,每行两个整数u,v表示有一条双向边连通了u,v两点
Output
输出一行两个整数 cnt,tot。其中,cnt 表示最少出口数,tot表示在出口数最少的情况下,设置出口的方案数在模998244353意义下的值
Note
对于 20% 的数据,n≤15
对于 40% 的数据,n≤10000
对于 68% 的数据,n≤100000
对于全部数据,n≤2000000 ,数据有梯度
保证有 16% 的数据满足,该图任意两点间至少有两条点不重复的路径
保证无自环,但不保证无重边
题解
看到题很容易想到割点,割点把图分成很多点连通分量。
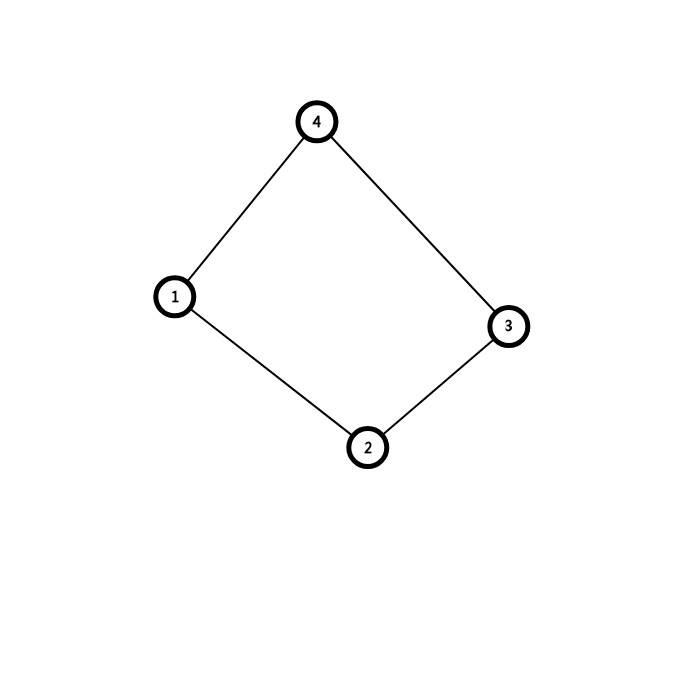
如果没有割点,那么需要选两个点,只选一个点的话,如果那个点被蹲就没地方出去了。方案数c(2,num)
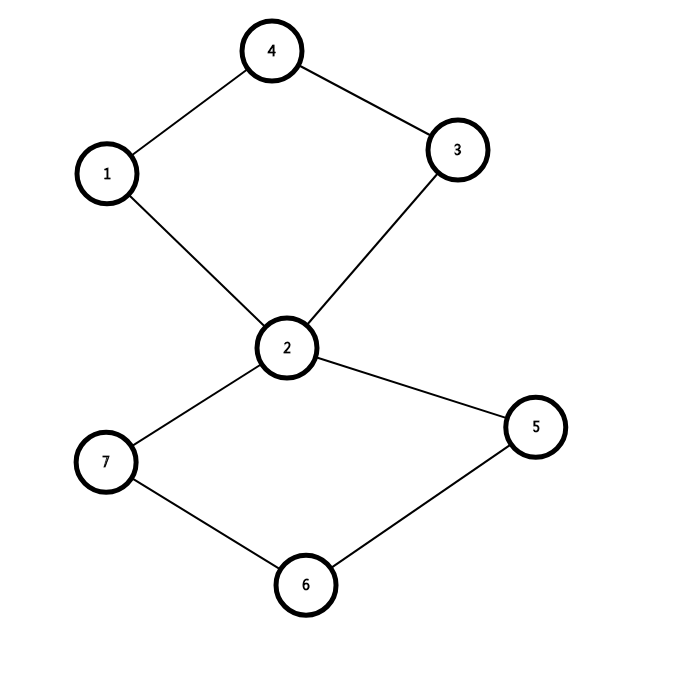
对于上或下两个连通分量,他们都有一个割点,只需要选一个出口,如果蹲割点,就可以在各自出口出;蹲自己的出口,就可以去对面的出口。
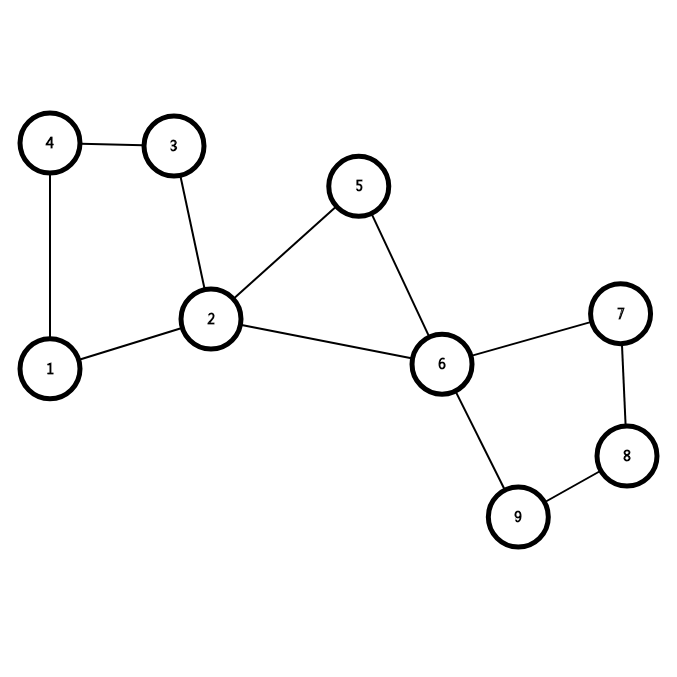
对于(2,5,6)中间这个连通分量,有两个割点,不需要选出口,因为可以到旁边的连通分量去。
所以先tarjan求出割点,再遍历每个连通分量,根据割点个数分类即可。

#include<bits/stdc++.h> using namespace std; #define ll long long const int maxn=2000005; const int mod=998244353; int n,m,cur; ll timer,num,cnt; ll ans1,ans2=1; int dfn[maxn],low[maxn]; int vis[maxn]; bool cut[maxn]; vector<int>e[maxn]; template<class T>inline void read(T &x){ x=0;char ch=getchar(); while(!isdigit(ch)) ch=getchar(); while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();} } int max(int x,int y){return x>y ? x : y ;} int min(int x,int y){return x<y ? x : y ;} void tarjan(int u,int fa){ int son=0; low[u]=dfn[u]=++cur; for(unsigned int i=0;i<e[u].size();i++){ int v=e[u][i]; if(!dfn[v]){ tarjan(v,u); low[u]=min(low[v],low[u]); if((++son>1&&!fa)||(dfn[u]<=low[v]&&fa)) cut[u]=true; } else if(v!=fa) low[u]=min(low[u],dfn[v]); } } void dfs(int u){ vis[u]=timer; num++;//连通分量非割点 for(unsigned int i=0;i<e[u].size();i++){ int v=e[u][i]; if(cut[v]&&vis[v]!=timer){ cnt++;//割点 vis[v]=timer; } if(!vis[v]) dfs(v); } } int main(){ freopen("rabbit.in","r",stdin); freopen("rabbit.out","w",stdout); read(m); for(int i=1;i<=m;i++){ int x,y; read(x);read(y); e[x].push_back(y); e[y].push_back(x); n=max(n,max(x,y)); } for(int i=1;i<=n;i++) if(!dfn[i]){ cur=0; tarjan(i,0); } for(int i=1;i<=n;i++) if(!vis[i]&&!cut[i]){ ++timer; cnt=num=0; dfs(i); if(!cnt){ if(num==1)//孤点 ans1++; else{ ans1+=2; ans2=ans2*num*(num-1)/2%mod; } } else if(cnt==1){ ans1++; ans2=ans2*num%mod; } } printf("%lld %lld",ans1,ans2); }




