一类最优化问题的通用解法

有这样一类问题：给你若干个元素 \((a,b,c)\)，选出一些，要求它们的 \(a\) 满足一些条件，使得 \(\sum b\times \sum c\) 最小（大）。

通用解法：把每种选择方案看成坐标系上的一个点 \((\sum b,\sum c)\)。则就是拿一个反比例函数去切，最小的能切到点的反比例函数就是答案。

不难发现最优解一定在下凸包上。考虑如何快速求出这个凸包：先找出 \(\sum b,\sum c\) 最小的点，它们肯定在凸包上。

考虑一个分治过程。当前要找端点 \(A,B\) 之间在凸包上的点：

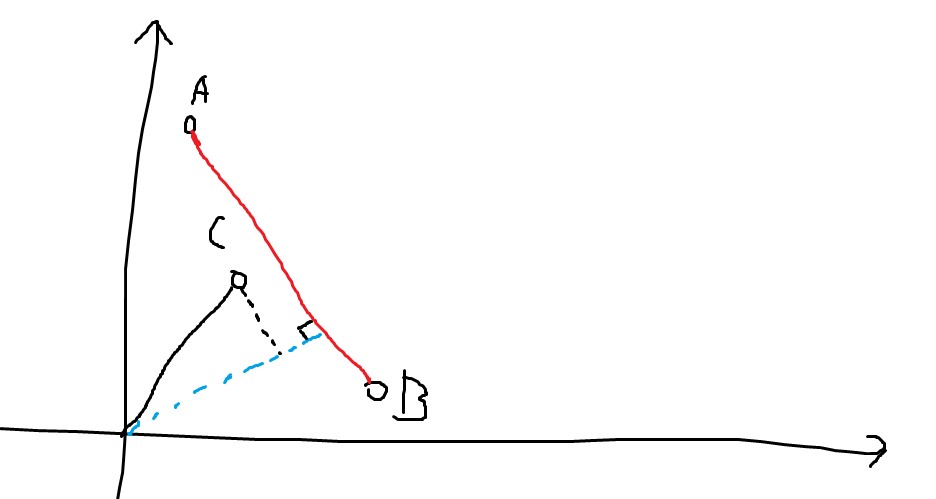
蓝色为 \(\overrightarrow{AB}\) 的法向量。如果 \(C\) 在凸包上，那么它在法向量上的投影一定小于 \(A,B\)。所以只需要找到投影最小的点，如果它等于 \(A\) 或 \(B\) 就说明 \(A,B\) 之间没有在凸包上的点。

求出 \(C\) 过后向两边递归分治下去即可。

凸包的期望点数是 \(\log\) 级别的，所以这种算法通常很快。