算法导论笔记（二）

本章开始介绍了堆的基本概念，然后引入最大堆和最小堆的概念。全章采用最大堆来介绍堆的操作，两个重要的操作是调整最大堆和创建最大堆，接着着两个操作引进了堆排序，最后介绍了采用堆实现优先级队列。

1、堆

　　堆给人的感觉是一个二叉树，但是其本质是一种数组对象，因为对堆进行操作的时候将堆视为一颗完全二叉树，树种每个节点与数组中的存放该节点值的那个元素对应。所以堆又称为二叉堆，堆与完全二叉树的对应关系如下图所示：

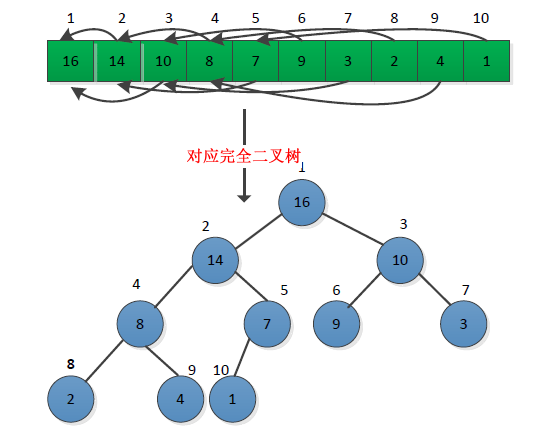
　　通常给定节点i，可以根据其在数组中的位置求出该节点的父亲节点、左右孩子节点，这三个过程一般采用宏或者内联函数实现。书上介绍的时候，数组的下标是从1开始的，所有可到：PARENT(i)=i/2　　LEFT(i) = 2*i 　　RIGHT(i) = 2*i+1。

　　根据节点数值满足的条件，可以将分为最大堆和最小堆。最大堆的特性是：除了根节点以外的每个节点i，有A[PARENT(i)] >= A[i],最小堆的特性是：除了根节点以外的每个节点i，有A[PARENT(i)] >=A[i]。

　　把堆看成一个棵树，有如下的特性：

（1）含有n个元素的堆的高度是lgn。

（2）当用数组表示存储了n个元素的堆时，叶子节点的下标是n/2+1，n/2+2，……，n。

（3）在最大堆中，最大元素该子树的根上；在最小堆中，最小元素在该子树的根上。

2、保持堆的性质

　　堆个关键操作过程是如何保持堆的特有性质，给定一个节点i，要保证以i为根的子树满足堆性质。书中以最大堆作为例子进行讲解，并给出了递归形式的保持最大堆性的操作过程MAX-HEAPIFY。先从看一个例子，操作过程如下图所示：

从图中可以看出，在节点i=2时，不满足最大堆的要求，需要进行调整，选择节点2的左右孩子中最大一个进行交换，然后检查交换后的节点i=4是否满足最大堆的要求，从图看出不满足，接着进行调整，直到没有交换为止。书中给出了递归形式的为代码，我用C语言实现如下所示：

void adjust_max_heap_recursive(int *datas,int length,int i)
{
    int left,right,largest;
    int temp;
    left = LEFT(i);   //left child
    right = RIGHT(i); //right child
    //find the largest value among left and rihgt and i.
    if(left<=length && datas[left] > datas[i])
        largest = left;
    else
        largest = i;
    if(right <= length && datas[right] > datas[largest])
        largest = right;
    //exchange i and largest
    if(largest != i)
    {
        temp = datas[i];
        datas[i] = datas[largest];
        datas[largest] = temp;
        //recursive call the function,adjust from largest
        adjust_max_heap(datas,length,largest);
    }
}

　　课后习题要求给出其非递归的形式，我想了半天，才搞出来，领悟能力有限啊。非递归就要考虑要循环进行实现，需要考虑的是循环结束条件是什么。对一个给定的节点i，要对其进行调整使其满足最大堆的性质。总的思想是先找出节点i的左右孩子节点，然后从三者中找到最大的节点，如果找到的最大节点就是i，说明i节点满足堆的性质，此时循环就结束了。如果找到的最大节点不是节点i，那么这个时候就要将最大的节点（设为largest）与节点i进行交换，然后从largest节点开始循环进行调整，直到满足条件为止。给出非递归的调整堆程序如下：

void adjust_max_heap(int *datas,int length,int i)
{
    int left,right,largest;
    int temp;
    while(1)
    {
        left = LEFT(i);   //left child
        right = RIGHT(i); //right child
        //find the largest value among left and rihgt and i.
        if(left <= length && datas[left] > datas[i])
            largest = left;
        else
            largest = i;
        if(right <= length && datas[right] > datas[largest])
            largest = right;
        //exchange i and largest
        if(largest != i)
        {
            temp = datas[i];
            datas[i] = datas[largest];
            datas[largest] = temp;
            i = largest;
            continue;
        }
        else
            break;
    }
}

 3、建堆

　　建立最大堆的过程是自底向上地调用最大堆调整程序将一个数组A[1.....N]变成一个最大堆。将数组视为一颗完全二叉树，从其最后一个非叶子节点（n/2）开始调整。调整过程如下图所示：

 

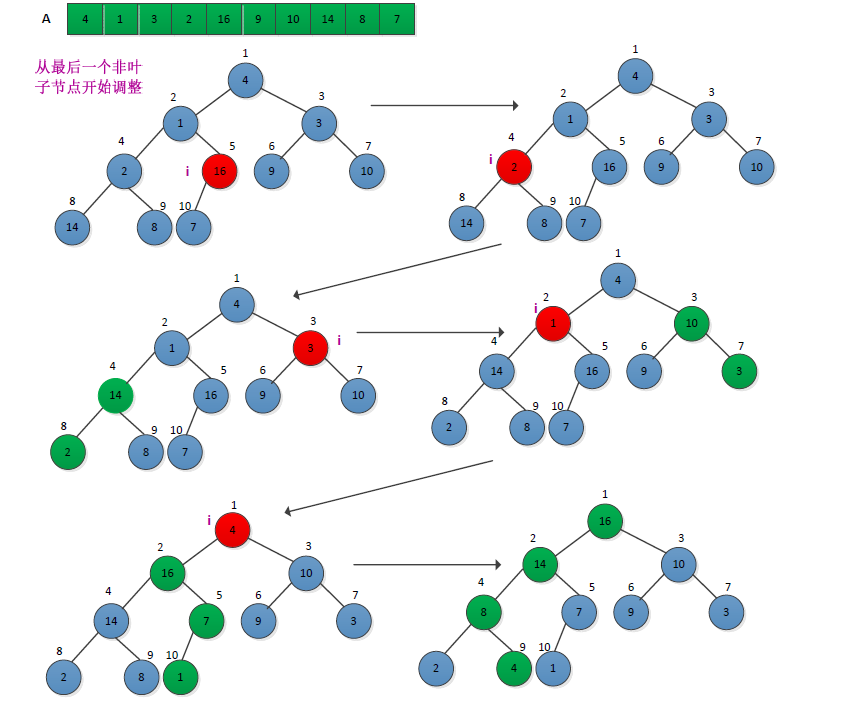
 书中给出了创建堆的为代码，我用C语言实现如下：

void build_max_heap(int *datas,int length)
{
    int i;
    //build max heap from the last parent node
    for(i=length/2;i>0;i--)
       adjust_max_heap(datas,length,i);
}

4、堆排序算法
　　堆排序算法过程为：先调用创建堆函数将输入数组A[1...n]造成一个最大堆，使得最大的值存放在数组第一个位置A[1]，然后用数组最后一个位置元素与第一个位置进行交换，并将堆的大小减少1，并调用最大堆调整函数从第一个位置调整最大堆。给出堆数组A={4,1,3,16,9,10,14,8,7}进行堆排序简单的过程如下：

（1）创建最大堆，数组第一个元素最大，执行后结果下图：

（2）进行循环，从length(a)到2，并不断的调整最大堆，给出一个简单过程如下：

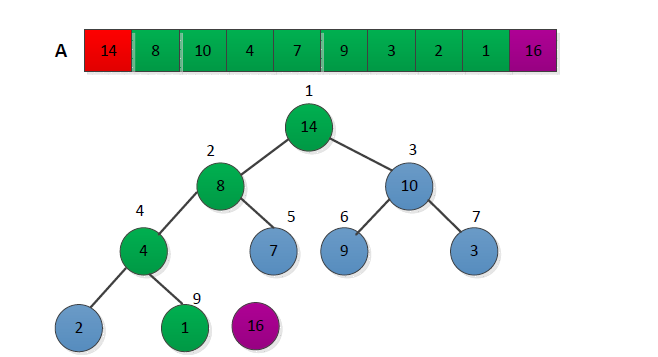
书中给出了对排序为代码，我用C语言实现如下所示

 void heap_sort(int *datas,int length)
 {
     int i,temp;
     //bulid max heap
     build_max_heap(datas,length);
     i=length;
     //exchange the first value to the last unitl i=1
     while(i>1)
     {
         temp = datas[i];
         datas[i] = datas[1];
         datas[1] =temp;
         i--;
         //adjust max heap,make sure the fisrt value is the largest
         adjust_max_heap(datas,i,1);
     }
}

 　　结合上面的调整堆和创建堆 的过程，写个简单测试程序连续堆排序，程序如下所示：

#include <stdio.h>
#include <stdlib.h>

//array's index begins 1,not 0

#define PARENT(i)  (i/2)
#define LEFT(i)    (i*2)
#define RIGHT(i)   (i*2+1)
#define NOTNUSEDATA   -65536

void adjust_max_heap(int *datas,int length,int i);
void adjust_max_heap_recursive(int *datas,int length,int i);
void build_max_heap(int *datas,int length);
void heap_sort(int *datas,int length);

int main()
{
    int i;
    //array's index begin 1
    int datas[11] = {NOTNUSEDATA,5,3,17,10,84,19,6,22,9,35};
    heap_sort(datas,10);
    for(i=1;i<11;++i)
        printf("%d ",datas[i]);
    printf("\n");
    exit(0);
}

void adjust_max_heap_recursive(int *datas,int length,int i)
{
    int left,right,largest;
    int temp;
    left = LEFT(i);   //left child
    right = RIGHT(i); //right child
    //find the largest value among left and rihgt and i.
    if(left<=length && datas[left] > datas[i])
        largest = left;
    else
        largest = i;
    if(right <= length && datas[right] > datas[largest])
        largest = right;
    //exchange i and largest
    if(largest != i)
    {
        temp = datas[i];
        datas[i] = datas[largest];
        datas[largest] = temp;
        //recursive call the function,adjust from largest
        adjust_max_heap(datas,length,largest);
    }
}
void adjust_max_heap(int *datas,int length,int i)
{
    int left,right,largest;
    int temp;
    while(1)
    {
        left = LEFT(i);   //left child
        right = RIGHT(i); //right child
        //find the largest value among left and rihgt and i.
        if(left <= length && datas[left] > datas[i])
            largest = left;
         else
            largest = i;
        if(right <= length && datas[right] > datas[largest])
            largest = right;
        //exchange i and largest
        if(largest != i)
        {
            temp = datas[i];
            datas[i] = datas[largest];
            datas[largest] = temp;
            i = largest;
            continue;
        }
        else
            break;
    }
}
void build_max_heap(int *datas,int length)
{
    int i;
    //build max heap from the last parent node
   for(i=length/2;i>0;i--)
        adjust_max_heap(datas,length,i);
}
void heap_sort(int *datas,int length)
{
    int i,temp;
    //bulid max heap
    build_max_heap(datas,length);
    i=length;
     //exchange the first value to the last unitl i=1
    while(i>1)
    {
        temp = datas[i];
        datas[i] = datas[1];
        datas[1] =temp;
        i--;
        //adjust max heap,make sure the fisrt value is the largest
        adjust_max_heap(datas,i,1);
    }
}

　　

程序测试结果如下所示：

从结果可以看出按照最大堆进行堆排序最终使得结果是从小到大排序（非递减的）。

堆排序算法时间复杂度：调整堆过程满足递归式T(n)<=T(2n/3)+θ(1)，有master定义可以知道T(n) = O(lgn)，堆排序过程中执行一个循环，调用最大堆调整函数，总的时间复杂度为O(nlgn）。

5、问题

（1）在创建最大堆的过程中，为什么从最后一个非叶子节点（n/2）开始到第一个非叶子（1）结束，而不是从第一个非叶子节点（1）到最后一个非叶子节点（n/2）结束呢？

我的想法是：如果是从第一个非叶子节点开始创建堆，有可能导致创建的堆不满足堆的性质，使得第一个元素不是最大的。这样做只是使得该节点的和其左右孩子节点满足堆性质，不能确保整个树满足堆的性质。如果最大的节点在叶子节点，那么将可能不会出现在根节点中。例如下面的例子：

从图中可以看出，从第一个非叶子节点开始创建最大堆，最后得到的结果并不是最大堆。而从最后一个非叶子节点开始创建堆时候，能够保证该节点的子树都满足堆的性质，从而自底向上进行调整堆，最终使得满足最大堆的性质。

 

 

第六章：优先级队列

1、概述

　　队列是一种满足先进先出（FIFO）的数据结构，数据从队列头部取出，新的数据从队列尾部插入，数据之间是平等的，不存在优先级的。这个就类似于普通老百姓到火车站排队买票，先来的先买票，每个人之间是平等的，不存在优先的权利，整个过程是固定不变的。而优先级队列可以理解为在队列的基础上给每个数据赋一个权值，代表数据的优先级。与队列类似，优先级队列也是从头部取出数据，从尾部插入数据，但是这个过程根据数据的优先级而变化的，总是优先级高的先出来，所以不一定是先进先出的。这个过就类似于买火车票时候军人比普通人优先买，虽然军人来的晚，但是军人的优先级比普通人高，总是能够先买到票。通常优先级队列用在操作系统中的多任务调度，任务优先级越高，任务优先执行（类似于出队列），后来的任务如果优先级比以前的高，则需要调整该任务到合适的位置，以便于优先执行，整个过程总是使得队列中的任务的第一任务的优先级最高。

　　优先级队列有两种：最大优先级队列和最小优先级队列，这两种类别分别可以用最大堆和最小堆实现。书中介绍了基于最大堆实现的最大优先级队列。一个最大优先级队列支持的操作如下操作：

INSERT(S,x)：把元素x插入到集合S

MAXIMUM(S)：返回S中具有最大关键字的元素

EXTRACT_MAX(S)：去掉并返回S中的具有最大关键字的元素

INCREASE_KEY(S,x,k)：将元素x的关键字的值增加到k，这里k值不能小于x的原关键字的值。

2、最大优先级队列操作实现

　　采用最大堆实现最大优先级队列，关于最大堆可以参见上文。

（1）HEAP_MAXIMUM用O(1)时间实现MAXIMUM(S)操作，即返回最大堆第一个元素的值即可（return A[1])。

（2）HEAP_EXTRACT_MAX实现EXTRACT_MAX操作，删除最大堆中第一个元素，然后调整堆。操作过程如下：将最堆中最后一个元素复制到第一个位置，删除最后一个节点（将堆的大小减少1），然后从第一个节点位置开始调整堆，使得称为新的最大堆。操作过程如下图所示：

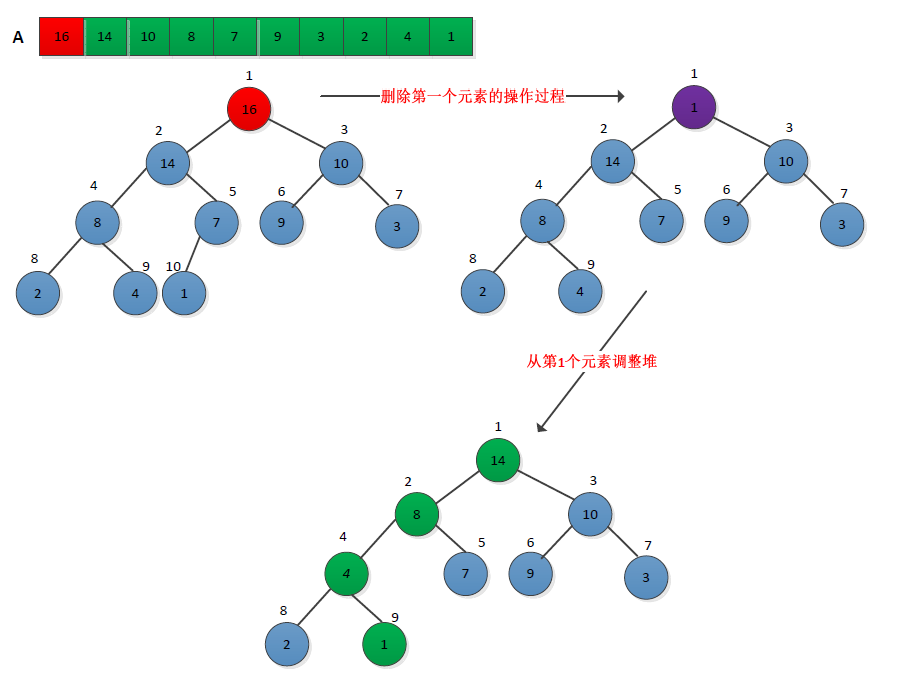
伪代码描述如下：

HEAD_EXTRACT_MAX(A)
 if heap_size[A]<1
   ther error
 max = A[1]
 A[1] = A[heap_size[A]];
 heap_size[A] = heap_size[A]-1
 adjust_max_heap(A,1)
 return MAX

（3）HEAP_INCREASE_KEY实现INCREASE_KEY，通过下标来标识要增加的元素的优先级key，增加元素后需要调整堆，从该节点的父节点开始自顶向上调整。操作过程如下图所示：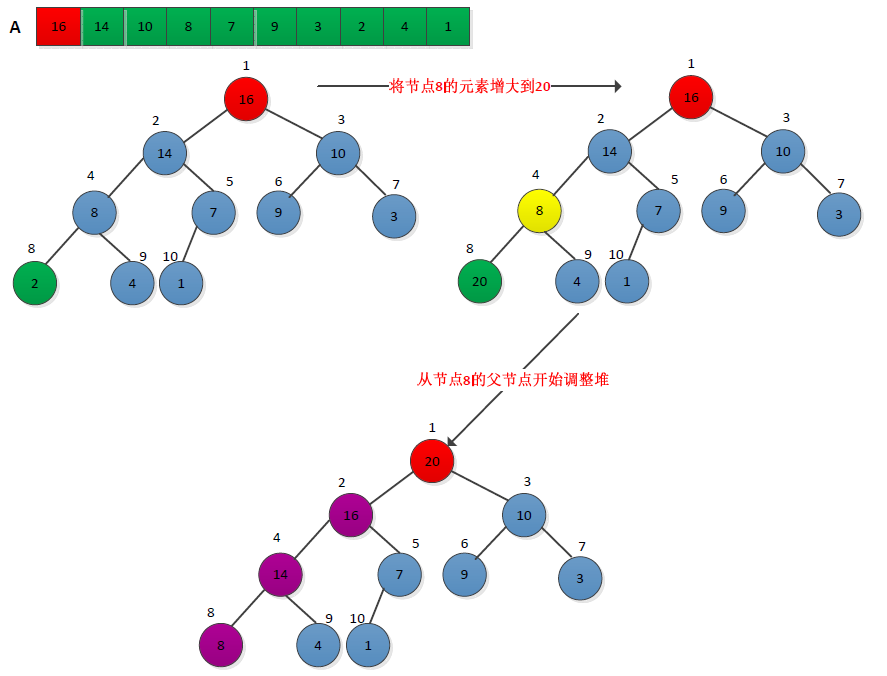

伪代码描述如下：

HEAP_INCREASE_KEY(A,i,key)
   if key < A[i]
     then error
   A[i] = key
  while i>1 && A[PARENT(i)] <A[i]
       do exchange A[i] <-> A[PARENT(i)]
       i = PARENT(i)

（4）MAX_HEAP_INSERT实现INSERT操作，向最大堆中插入新的关键字。新的关键字插入在优先级的队尾部，然后从尾部的父节点开始自顶向上调整堆伪代码描述如下：

MAX_HEAP_INSERT(A,key)
  heap_size[A] = heap_size[A]+1
  A[heap_size[A]] = -0;
  HEAP_INCREASE_KEY(A,heap_size[A],key)

 3、实例

　问题描述如下：优先级队列中有多个事件发生，每个事件有自己独立的优先级，优先级是非负数，数值越大优先级越高。采用最大优先级队列模拟事件执行的优先顺序。具体操作包括：

（1）向优先级队列中添加一个新事件

（2）获取优先级队列中优先级最高的事件

（3）删除优先级队列中指定位置的事件

（4）增加优先级队列中指定位置事件的优先级

（5）降低优先级队列中指定位置事件的优先级

采用C++语言实现，完整程序如下所示：

#include <iostream>
#include <string>
#include <cstdlib>
using namespace std;

const static int QUEUELEN = 100;

class Event
{
public:
    Event():eventname(""),priority(-1){};
    Event(const string &en,const int p):eventname(en),priority(p){};
    Event(const Event& en)
    {
        eventname = en.eventname;
        priority = en.priority;
    }
    ~Event(){};
    int get_event_priority()const
    {
        return priority;
    }
    string get_event_name()const
    {
        return eventname;
    }
    void increase_event_priority(const int k)
    {
        priority = priority + k;
    }
    void decrease_event_priority(const int k)
    {
         priority = priority - k;
    }
    void show_event() const
    {
        cout<<"Eventname is: ("<<eventname<<") and the priority is: "<<priority<<endl;
    }
private:
    string eventname;
    int priority;
};
class PriorityQueue
{
public:
    PriorityQueue();
    void adjust_event(int index);
    Event get_event()const;
    void insert_event(const Event& en);
    void increase_event_priority(int pos,int k);
    Event delete_event(int pos);
    void show_events() const;
    ~PriorityQueue();
private:
    Event *events;
    int length;
 };

PriorityQueue::PriorityQueue()
{
    events = new Event[QUEUELEN];
    length = 0;
}

PriorityQueue::~PriorityQueue()
{
    if(!events)
         delete [] events;
    length = 0;
}
//adjust max heap 
void PriorityQueue::adjust_event(int index)
{
    int left,right,largest;
    Event temp;
    while(1)
    {
        left = index*2;
        right = index*2+1;
        if(left <= length &&
           events[left].get_event_priority() > events[index].get_event_priority())
            largest = left;
        else
            largest = index;
        if(right <= length &&
           events[right].get_event_priority() > events[largest].get_event_priority())
            largest = right;
        if(largest != index)
        {
            temp = events[index];
            events[index] = events[largest];
            events[largest] = temp;
            index = largest;
        }
        else
            break;
    }
}
Event PriorityQueue::get_event()const
{
    if(length != 0)
        return events[1];
    else
        return Event();
}

void PriorityQueue::insert_event(const Event& en)
{
    length = length + 1;
    events[length] = en;
    increase_event_priority(length,0);
}

void PriorityQueue::increase_event_priority(int pos,int k)
{
    int i,parent;
    Event temp;
    if(pos > length)
    {
        cout<<"error: the pos index is larger than queue length"<<endl;
        return;
    }
    events[pos].increase_event_priority(k);
    i = pos;
    parent = i/2;
    while(i>1
          && events[parent].get_event_priority() < events[i].get_event_priority())
    {
        temp = events[i];
        events[i] = events[parent];
        events[parent] = temp;
        i = parent;
        parent = i/2;
    }
}

Event PriorityQueue::delete_event(int pos)
{
    Event reten;
    if(pos > length)
    {
        cout<<"Error:pos index is larger than queue length"<<endl;
        return reten;
    }
    reten = events[pos];
    events[pos] = events[length];
    length--;
    adjust_event(pos);
    return reten;
}
void PriorityQueue::show_events() const
{
    if(length == 0)
    {
        cout<<"There is no any event in the priority queue"<<endl;
    }
    else
    {
        cout<<"There are "<<length<<" events in the priority queue."<<endl;
        for(int i=1;i<=length;i++)
        {
            events[i].show_event();
        }
    }

}
int main()
{
    PriorityQueue pqueue;
    Event en;
    Event en1("fork",2);
    Event en2("exec",3);
    Event en3("wait",1);
    Event en4("signal",6);
    Event en5("pthread_create",5);
    pqueue.insert_event(en1);
    pqueue.insert_event(en2);
    pqueue.insert_event(en3);
    pqueue.insert_event(en4);
    pqueue.insert_event(en5);
    pqueue.show_events();
    cout<<"\nThe max priority event is: "<<endl;
    en = pqueue.get_event();
    en.show_event();
    cout<<"\nIncrese event3 by 7"<<endl;
    pqueue.increase_event_priority(3,7);
    en = pqueue.get_event();
    en.show_event();
    pqueue.show_events();
    cout<<"\nDelete the first event:"<<endl;
    pqueue.delete_event(1);
    pqueue.show_events();
    exit(0);
}

　　

程序测试结果如下所示：

4、问题

（1）如何使用优先级队列实现一个先进先出的队列和先进后出的栈？

　　我的想法是：队列中的元素是先进先出（FIFO）的，因此可以借助最小优先级队列实现队列。具体思想是，给队列中的每个元素赋予一个权值，权值从第一个元素到最后一个依次递增（如果采用数组实现的话，可以用元素所在的下标作为优先级，优先级小的先出队列），元素出队列操作每次取优先级队列第一个元素，取完之后需要堆最小优先级队列进行调整，使得第一个元素的优先级最小。栈中的元素与队列刚好相反，元素是先进后出（FILO），因此可以采用最大优先级队列进行实现，与用最小优先级队列实现队列思想类似，按照元素出现的顺序进行标记元素的优先级，数据越是靠后，优先级越高。

　　举例说明采用最小优先级队列实现先进先出队列，现在有一组数A={24,15,27,5,43,87,34}共六个数，假设数组下标从1开始，以元素所在数组中的下标为优先级创建优先级队列，队列中元素出入时候调整最小优先级队列。操作过程如下图所示：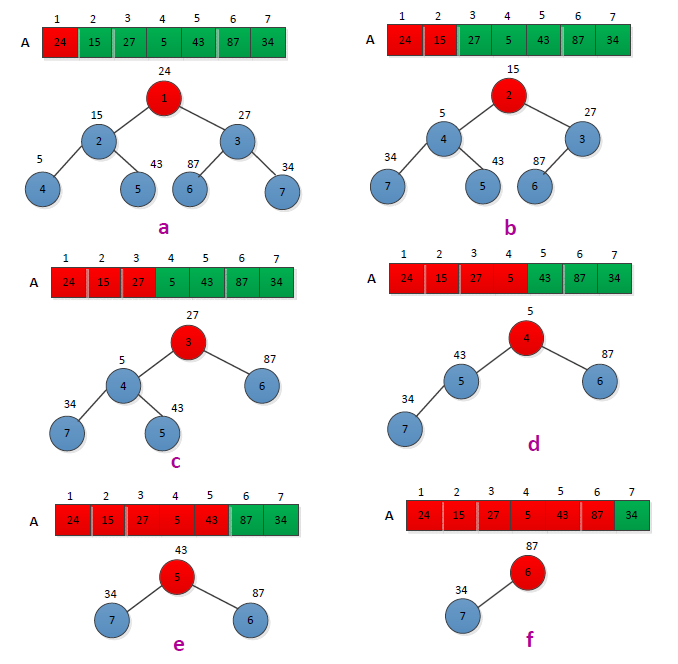

练习6.5.8：最小堆K路合并

　《算法导论》第六章主要内容是关于堆和优先级队列，书中给出了一个练习题，非常有有意思，今天好好研究练习一下。题目如下：请给出一个时间为O(nlgk)、用来将k个已排序链表合并为一个排序链表的算法。此处n为所有输入链表中元素的总数。（提示：用一个最小堆来做k路合并）。

　　看到题目第个想到的是归并排序过程中的归并操作子过程，从头开始两两比较，找出最小的，然后接着往后比较，常用的是2路归并。而题目给的是k个已排好序的链表(k>=2)。如果没有提示，我半天不知道如何去实现，幸好提示说用最小堆来做k路合并，于是我想到可以这样做：创建一个大小为k的数组，将k个链表中的第一个元素依次存放到数组中，然后将数组调整为最小堆，这样保证数组的第一个元素是最小的，假设为min，将min从最小堆取出并存放到最终结果的链表中，此时将min所在链表的下一个元素到插入的最小堆中，继续上面的操作，直到堆中没有元素为止。举个例子如下图所示（只给出不部分操作）：

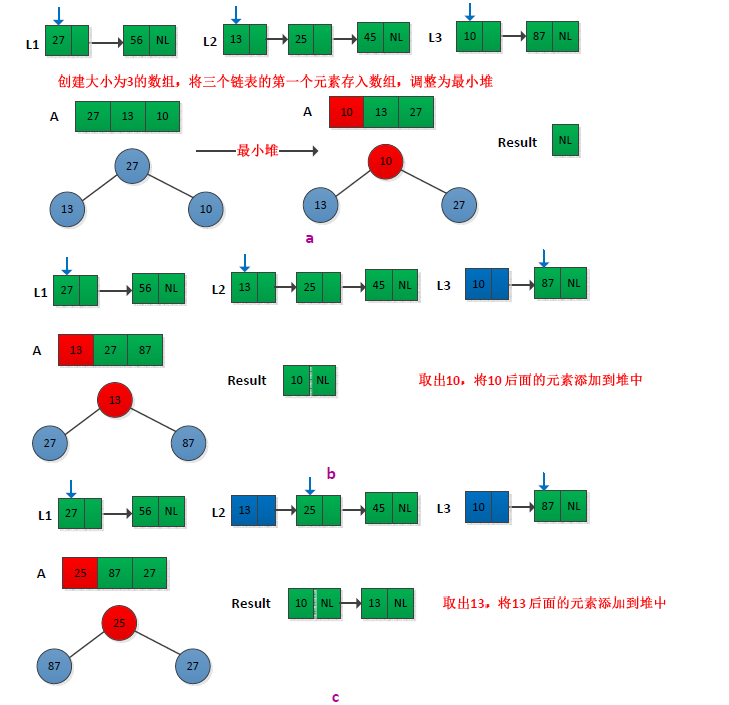
最终结果如下图所示：

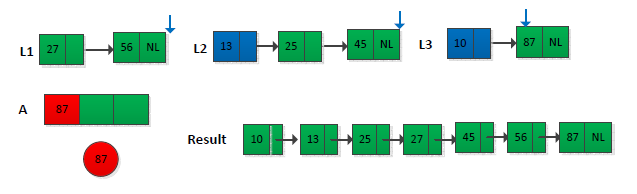
现在采用C++语言，借助STL实现此过程，链表采用list，最小堆中存放的是list的迭代器，表示list中元素的位置。完整程序如下：

#include <iostream>
#include <vector>
#include <list>
#include <iterator>
#include <cstdlib>
using namespace std;

template<class T> class MinHeap
{
public:
    MinHeap();
    MinHeap(const size_t size);
    ~MinHeap();
    T get_min() const;
    void delete_min();
    void insert_element(const T& e);
    void adjust_min_heap(const size_t i);
    size_t get_heap_size() const;
    int compare(const T& t1,const T& t2);
private:
    T *heap;
    size_t heap_size;
};

template<class T>
MinHeap<T>::MinHeap():heap(NULL),heap_size(0){}

template<class T>
MinHeap<T>::MinHeap(const size_t size)
{
    if(!heap)
        delete [] heap;
    heap = new T[size+1];
    heap_size = 0;
}

template<class T>
MinHeap<T>::~MinHeap()
{
    if(!heap)
        delete [] heap;
    heap_size = 0;
}

template<class T>
T MinHeap<T>::get_min() const
{
    if(heap_size > 0)
        return heap[1];
    else
        return T();
}

template<class T>
void MinHeap<T>::delete_min()
{
    if(heap_size > 0)
    {
        heap[1] = heap[heap_size];
        heap_size = heap_size - 1;
        adjust_min_heap(1);
    }
    else
    {
        cout<<"Error: the min heap is empty"<<endl;
    }
}

template<class T>
void MinHeap<T>::insert_element(const T& e)
{
    size_t i,parent;
    T temp;
    heap_size = heap_size + 1;
    heap[heap_size] = e;
    i = heap_size;
    parent = i/2;
    while(i>1 && compare(heap[parent],heap[i]) > 0)
    {
        temp = heap[parent];
        heap[parent] = heap[i];
        heap[i] = temp;
        i = parent;
        parent = i/2;
    }
}

template<class T>
void MinHeap<T>::adjust_min_heap(const size_t i)
{
    size_t left,right,least;
    T temp;
    left = i*2;
    right = i*2+1;
    if(left <= heap_size && compare(heap[left],heap[i]) < 0)
        least = left;
    else
        least = i;
    if(right <= heap_size && compare(heap[right],heap[least]) < 0)
        least = right;
    if(least != i)
    {
        temp = heap[least];
        heap[least] = heap[i];
        heap[i] = temp;
        adjust_min_heap(least);
    }
}
template<class T>
size_t MinHeap<T>::get_heap_size() const
{
    return heap_size;
}

template<class T>
int MinHeap<T>::compare(const T& t1,const T& t2)
{
    return (*t1-*t2);
}

const static int k = 3;

int main()
{

    list<int> lists[k];
    list<int>::iterator iters[k];
    list<int> retlist;
    list<int>::iterator retiter;
    list<int>::iterator iter;
    MinHeap<list<int>::iterator> minheap(k);

    //first list <12,24,52>
    lists[0].push_back(12);
    lists[0].push_back(24);
    lists[0].push_back(52);
    cout<<"First list: ";
    for(iter=lists[0].begin();iter != lists[0].end();++iter)
          cout<<*iter<<"->";
    cout<<"NULL"<<endl;
    //second list <9,32>
    lists[1].push_back(9);
    lists[1].push_back(32);
    cout<<"Second list: ";
    for(iter=lists[1].begin();iter != lists[1].end();++iter)
          cout<<*iter<<"->";
    cout<<"NULL"<<endl;
    //third list <34,42,78>
    lists[2].push_back(34);
    lists[2].push_back(42);
    lists[2].push_back(78);
    cout<<"Third list: ";
    for(iter=lists[2].begin();iter != lists[2].end();++iter)
          cout<<*iter<<"->";
    cout<<"NULL"<<endl;
    iters[0] = lists[0].begin();
    iters[1] = lists[1].begin();
    iters[2] = lists[2].begin();

    minheap.insert_element(iters[0]);
    minheap.insert_element(iters[1]);
    minheap.insert_element(iters[2]);

    while(minheap.get_heap_size())
    {
        iter = minheap.get_min() ;
        retlist.push_back(*iter);
        minheap.delete_min();
        ++iter;
        if(iter != lists[0].end() && iter != lists[1].end()
           &&iter != lists[2].end())
            minheap.insert_element(iter);
    }
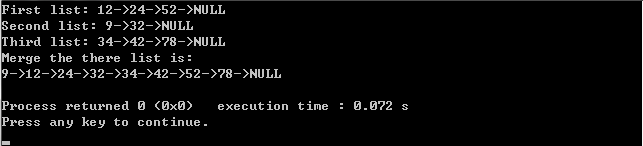
    cout<<"Merge the there list is: "<<endl;
    for(retiter = retlist.begin();retiter!= retlist.end();retiter++)
        cout<<*retiter<<"->";
    cout<<"NULL"<<endl;
    exit(0);
}

　　

程序测试结果如下所示：