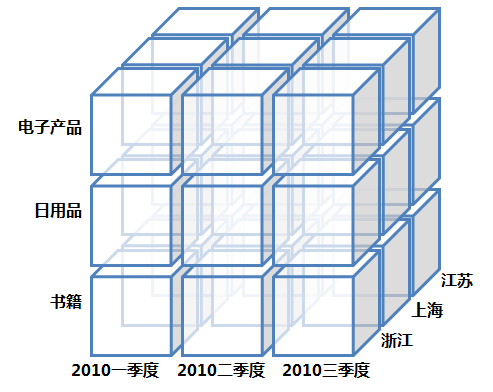
数据立方体（Cube）

 

 

如上图所示，这是由三个维度构成的一个OLAP立方体，立方体中包含了满足条件的cell(子立方块)值，这些cell里面包含了要分析的数据，称之为度量值。显而易见，一组三维坐标唯一确定了一个子立方。

 

多位模型的基本概念介绍：

 

•  立方体：由维度构建出来的多维空间，包含了所有要分析的基础数据，所有的聚合数据操作都在立方体上进行。
•  维度：就是观察数据的一种角度。在这个例子中，路线，源，时间都是维度，
•  这三个维度构成了一个立方体空间。维度可以理解为立方体的一个轴。要注意的是有一个特殊的维度，即度量值维度。
•  维度成员：构成维度的基本单位。对于时间维，它的成员分别是：第一季度、第二季度、第三季度、第四季度。
•  层次：维度的层次结构，要注意的是存在两种层次：自然层次和用户自定义层次。对于时间维而言，(年、月、日)是它的一个层次，(年、季度、月)是它的另一个层次，一个维可以有多个层次，层次可以理解为单位数据聚合的一种路径。
•  级别：级别组成层次。对于时间维的一个层次(年、月、日)而言，年是一个级别，月是一个级别，日是一个级别，显然这些级别是有父子关系的。
•  度量值：要分析展示的数据，即指标。如图1中一个cell中包含了两个度量值：装箱数和截至时间，可以对其进行多维分析。
•  事实表：存放度量值的表，同时存放了维表的外键。所有的分析用的数据最终都是来自与事实表。
•  维表：一个维度对应一个或者多个维表。一个维度对应一个维表时数据的组织方式就是采用的星型模式，对应多个维表时就是采用雪花模式。雪花模式是对星型模式的规范化。简言之，维表是对维度的描述。
•  MDX查询：多维模型的查询语言MDX(MDX是微软发布的多维查询语言标准),它的语法与SQL有很多相似之处：select {[Measures].[Salary]} on columns, {[Employee].[employeeId].members} on rows from CubeTest对于这条语句，COLUMNS 和 ROWS都代表查询轴，其中COLUMNS代表列轴，ROWS代表行轴。COLUMNS又可以写成0，ROWS又可以写成1，当只有两个查询轴时，可以理解为结果的展现格式是一个平坦二维表。这条语句的含义就是查询名字为CubeTest的立方体，列显示Measures维度的salary，行显示 Employee维度employeeId级别的所有成员，那么得出的结果就是employeeId所有成员的salary，也就是所有员工的薪酬。具体语法规范和帮助文档可以参考微软的用户文档。

 

 

多维数据模型是为了满足用户从多角度多层次进行数据查询和分析的需要而建立起来的基于事实和维的数据库模型，其基本的应用是为了实现OLAP（Online Analytical Processing）。

其中，每个维对应于模式中的一个或一组属性，而每个单元存放某种聚集度量值，如count或sum。数据立方体提供数据的多维视图，并允许预计算和快速访问汇总数据。

《数据挖掘：概念与技术》中例举如下模型

数据立方体允许以多维数据建模和观察。它由维和事实定义。 维是关于一个组织想要记录的视角或观点。每个维都有一个表与之相关联，称为维表。 事实表包括事实的名称或度量以及每个相关维表的关键字。

在数据仓库的研究文献中，一个n维的数据的立方体叫做基本方体。给定一个维的集合，我们可以构造一个方体的格，每个都在不同的汇总级或不同的数据子集显示数据，方体的格称为数据立方体。0维方体存放最高层的汇总，称为顶点方体；而存放最底层汇总的方体称为基本方体。

 

数据仓库的概念模型 最流行的数据仓库概念是多维数据模型。这种模型可以以星型模式，雪花模式，或事实星座模式的形式存在。

1.星型模式(Star schema):事实表在中心，周围围绕地连接着维表(每维一个)，事实表包含有大量数据，没有冗余。

2.雪花模式(Snowflake schema):是星型模式的变种，其中某些维表是规范化的，因而把数据进一步分解到附加表中。结果，模式图形成类似雪花的形状。

雪花模型相较于星座模型，是把维表进行了规范化。

 

事实星座(Fact constellations):多个事实表共享维表，这种模式可以看作星座模式集，因此称作星系模式(galaxy schema)，或者事实星座(fact constellation)

事实星座模式是把事实间共享的维进行合并。

对概念进行分层，有利于数据的汇总。

数据立方体

　　关于数据立方体（Data Cube），这里必须注意的是数据立方体只是多维模型的一个形象的说法。立方体其本身只有三维，但多维模型不仅限于三维模型，可以组合更多的维度，但一方面是出于更方便地解释和描述，同时也是给思维成像和想象的空间；另一方面是为了与传统关系型数据库的二维表区别开来，于是就有了数据立方体的叫法。所以本文中也是引用立方体，也就是把多维模型以三维的方式为代表进行展现和描述，其实上Google图片搜索“OLAP”会有一大堆的数据立方体图片，这里我自己画了一个：

OLAP

　　OLAP（On-line Analytical Processing，联机分析处理）是在基于数据仓库多维模型的基础上实现的面向分析的各类操作的集合。可以比较下其与传统的OLTP（On-line Transaction Processing，联机事务处理）的区别来看一下它的特点：

OLAP与OLTP

数据处理类型	OLTP	OLAP
面向对象	业务开发人员	分析决策人员
功能实现	日常事务处理	面向分析决策
数据模型	关系模型	多维模型
数据量	几条或几十条记录	百万千万条记录
操作类型	查询、插入、更新、删除	查询为主

OLAP的类型

　　首先要声明的是这里介绍的有关多维数据模型和OLAP的内容基本都是基于ROLAP，因为其他几种类型极少接触，而且相关的资料也不多。

MOLAP(Multidimensional)

　　即基于多维数组的存储模型，也是最原始的OLAP，但需要对数据进行预处理才能形成多维结构。

ROLAP(Relational)

　　比较常见的OLAP类型，这里介绍和讨论的也基本都是ROLAP类型，可以从多维数据模型的那篇文章的图中看到，其实ROLAP是完全基于关系模型进行存放的，只是它根据分析的需要对模型的结构和组织形式进行的优化，更利于OLAP。

HOLAP(Hybrid)

　　介于MOLAP和ROLAP的类型，我的理解是细节的数据以ROLAP的形式存放，更加方便灵活，而高度聚合的数据以MOLAP的形式展现，更适合于高效的分析处理。

　　另外还有WOLAP(Web-based OLAP)、DOLAP(Desktop OLAP)、RTOLAP(Real-Time OLAP)，具体可以参开维基百科上的解释——OLAP。

OLAP的基本操作

　　我们已经知道OLAP的操作是以查询——也就是数据库的SELECT操作为主，但是查询可以很复杂，比如基于关系数据库的查询可以多表关联，可以使用COUNT、SUM、AVG等聚合函数。OLAP正是基于多维模型定义了一些常见的面向分析的操作类型是这些操作显得更加直观。

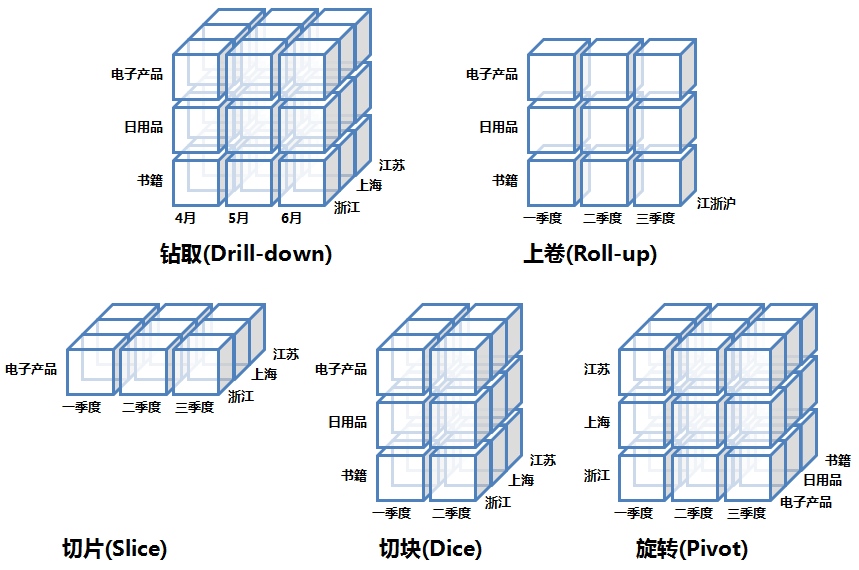
　　OLAP的多维分析操作包括：钻取（Drill-down）、上卷（Roll-up）、切片（Slice）、切块（Dice）以及旋转（Pivot），下面还是以上面的数据立方体为例来逐一解释下：

 

　　钻取（Drill-down）：在维的不同层次间的变化，从上层降到下一层，或者说是将汇总数据拆分到更细节的数据，比如通过对2010年第二季度的总销售数据进行钻取来查看2010年第二季度4、5、6每个月的消费数据，如上图；当然也可以钻取浙江省来查看杭州市、宁波市、温州市……这些城市的销售数据。

　　上卷（Roll-up）：钻取的逆操作，即从细粒度数据向高层的聚合，如将江苏省、上海市和浙江省的销售数据进行汇总来查看江浙沪地区的销售数据，如上图。

　　切片（Slice）：选择维中特定的值进行分析，比如只选择电子产品的销售数据，或者2010年第二季度的数据。

　　切块（Dice）：选择维中特定区间的数据或者某批特定值进行分析，比如选择2010年第一季度到2010年第二季度的销售数据，或者是电子产品和日用品的销售数据。

　　旋转（Pivot）：即维的位置的互换，就像是二维表的行列转换，如图中通过旋转实现产品维和地域维的互换。

OLAP的优势

　　首先必须说的是，OLAP的优势是基于数据仓库面向主题、集成的、保留历史及不可变更的数据存储，以及多维模型多视角多层次的数据组织形式，如果脱离的这两点，OLAP将不复存在，也就没有优势可言。

数据展现方式

　　基于多维模型的数据组织让数据的展示更加直观，它就像是我们平常看待各种事物的方式，可以从多个角度多个层面去发现事物的不同特性，而OLAP正是将这种寻常的思维模型应用到了数据分析上。

查询效率

　　多维模型的建立是基于对OLAP操作的优化基础上的，比如基于各个维的索引、对于一些常用查询所建的视图等，这些优化使得对百万千万甚至上亿数量级的运算变得得心应手。

分析的灵活性

　　我们知道多维数据模型可以从不同的角度和层面来观察数据，同时可以用上面介绍的各类OLAP操作对数据进行聚合、细分和选取，这样提高了分析的灵活性，可以从不同角度不同层面对数据进行细分和汇总，满足不同分析的需求。

 

 

SSAS中Cube的结构

在SSAS（SQL Server Analysis Services）中构建Cube和编写MDX的时候，我们很容易被一些名词弄糊涂，比如：Dimension（维度），Measures Dimension（度量维度），Measure（度量），Hierarchy（层次结构），Attribute hierarchy（属性层次结构），Level（级别），Cell（单元），Member（成员），Member Property（成员属性），Set（集），Turple（元组）等等。要想弄清楚这些名词，就必须理解Cube的结构。
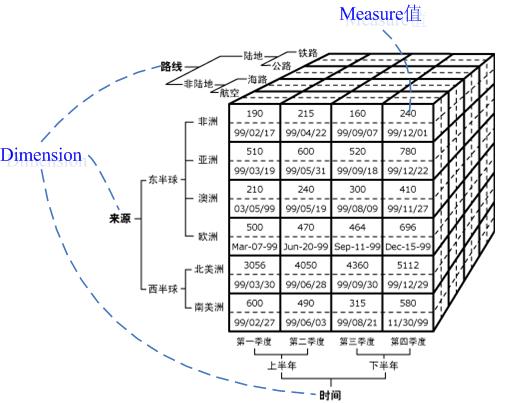
上述名词的解释详见：http://msdn2.microsoft.com/en-us/library/ms144884.aspx Cube、Dimension和Measure Cube就象一个坐标系，每一个Dimension代表一个坐标轴，要想得到一个点，就必须在每一个坐标轴上取的一个值，而这个点就是Cube中的Cell。见下图（来源于http://msdn2.microsoft.com/zh-cn/library/ms144884.aspx）：  
上图很好的说明了Cube、Dimension、Measure之间的关系。这里需要注意的是：其实Measure也属于一个维度，即Measures Dimension。所有的Measure构成了Measures Dimension，这个维度的只有一个Hierarchy，而且这个Hierarchy只有一个层次（Level）。
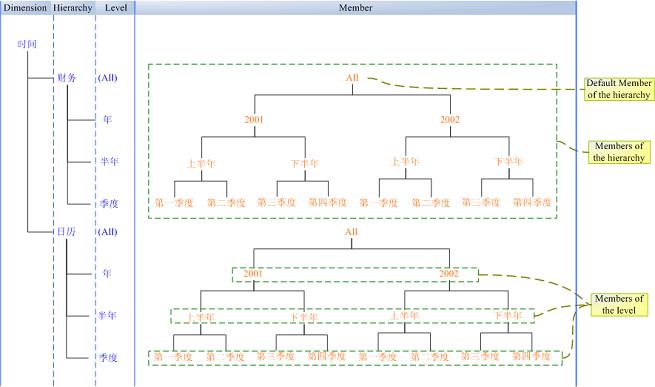
Hierarchy、Level和Memeber 在上节的图中，每个Dimension只有一个Hierarchy，而在实际的环境中，一个Dimension往往有很多Hierarchy。因此，上一小节中关于“Cube就象一个坐标系，每一个Dimension代表一个坐标轴”这句话其实不够准确，准确的说应该是每一个Hierarchy代表了一个坐标轴，而Hierarchy中每一个Member代表了坐标轴上的一个值。下图以时间维度为例展示了Dimension的内部结构。
此外，我们需要说明的是：

1) 上图中说明的是一般Dimension的结构，在实际的模型中，其实可以做很多自定义的工作。比如：我们可以修改Hierarchy的默认Member。 
2) 一般情况下，SSAS中Hierarchy的默认Member是All（在你的模型中，可能叫其他名称）。换句话说在MDX中[时间].[财政]等价于[时间].[财政].[All]，[时间].[财政].Children等价于[时间].[财政].[All].Children。
3) Dimension_Name.Hierarchy_Name.Level_Name等价于Dimension_Name.Hierarchy_Name.Level_Name.Members。比如：[时间].[财政].[半年]等价于[时间].[财政].[半年].Members。Level的Members是该级别的所有元素（对于[时间].[财政].[半年].Members={[上半年]，[下半年]，[上半年]，[下半年]}，其中前两个是2001年下的，后两个属于2002年），而Hierarchy的Members包含了该Hierarchy下所有的内容。
4) 当且仅当一个Dimension下只有一个Hierarchy，则Dimension_Name等价于Dimension_Name.Hierarchy_Name纬度。比方说：时间维度只有一个财务Hierarchy，则[时间]等价[时间].[财务]。
5) Attribute Hierarchy中Members的层次是两层（MSDN的说法更加准确，这里简化了一些）：第一层：All，第二层：叶子节点。也就是说它和多层的Hierarchy相比，两者结构完全相同，这是统一维度模型（Unified Dimensional Model）一个方面的体现。 
      注意：采用Attribute Hierarchy能够使编写MDX更加容易，但同时也增加了Cube的容量，加大了Cells的个数，对性能有负面影响。因此，在建模的时候，我们可以把一些Attribute Hierarchy的AttributeHierarchyEnabled属性设置成False，同时在编写MDX时，以Member Property的方式来引用，这样可以在满足需求的前提下提高性能。
6) Measures Dimension是一个特殊的维度，它的Members中没有All这个成员，它的默认Member可以在建模时指定。
7)对于一般的维度，其第一层Level的默认是“（All）”。
Turple和Set 如果说Cube好像一个坐标系，那么Turple、Set的关系就好比点和面的关系。Turple由Cube中每个Hierarchy的一个Member组成。由于Hierarchy的个数非常多，所以一般不可能在Turple表达式中把所有的Member都明确指定，故此，为了简化开发，所有没有明确指定Member的Hierarchy，用该Hierarchy的默认Member代替。也就是说：([时间].[财政].[2001].[上半年]) 等价于（[时间].[财政].[2001].[上半年]，[时间].[日历].[All]）。另外我们需要注意的：

1) 有的说法认为：Turple是“Cube 上的一个子集（不断开的子Cube），这个看法是不准确的，因为Turple只是一个点，不是面，它仅仅由每个Hierarchy的一个Member组成的。

2) 外面（）起来的表达式不一定是Turple。比如：（[时间].[财政].[半年].Members，[时间].[日历].[2001].[上半年]）就不是一个Turple，而是一个Set，其原因在于，Turple是点，它仅仅由每个Hierarchy的一个Member组成，如果在任何一个Hierarchy上有两个成员，则其就变成Set了。

      注意：（[时间].[财政].[半年].Members，[时间].[日历].[2001].[上半年]）等价于Crossjoin（[时间].[财政].[半年].Members，[时间].[日历].[2001].[上半年]）或{[时间].[财政].[半年].Members}*{[时间].[日历].[2001].[上半年]}，在SSAS的MDX中，我们可以在（）中定义多个用逗号分隔开的表达式，编译器会进行分析，如果发现是Set的话，就把它转化成多个Set相乘的形式。

3) Set中的Turple可以重复。比如：{[时间].[日历].[2001].[上半年]，[时间].[日历].[2001].[上半年]}并不等于{[时间].[日历].[2001].[上半年]}，因为前者有两个Turple，后者只有一个。

4) SSAS能够根据上下文的需要，自动把Turple变成Set，单个Member变成Turple，多个Member变成Set。这也是我们常常混淆Turple和Set的原因。详细的例子如下：

a）上下文需要Set时，（[时间].[日历].[2001].[上半年]）自动转化成{[时间].[日历].[2001].[上半年]}。  b）上下文需要Turple时，[时间].[日历].[2001].[上半年]自动转化成（[时间].[日历].[2001].[上半年]）。 c）上下文需要Set时，[时间].[日历].[2001].Children自动转化成{[时间].[日历].[2001].Children}。

总结 总体来看，SSAS中的Cube的内部结构非常的清晰，在实际开发中，只要多注意一下默认的一些转化，使用起来是很容易的。

 

 

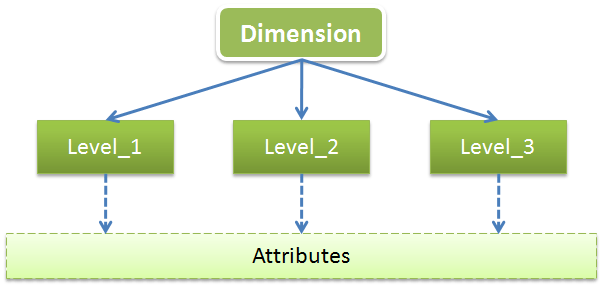
维（Dimension）

　　维是用于从不同角度描述事物特征的，一般维都会有多层（Level），每个Level都会包含一些共有的或特有的属性（Attribute），可以用下图来展示下维的结构和组成：

　　以时间维为例，时间维一般会包含年、季、月、日这几个Level，每个Level一般都会有ID、NAME、DESCRIPTION这几个公共属性，这几个公共属性不仅适用于时间维，也同样表现在其它各种不同类型的维。其中ID一般被视为代理主键（Agent），它只被用于作为唯一性标志，并且是多维模型中关联关系的代理者，在业务层面并不具有任何意义；NAME一般是业务主键（Business），在业务层面限制唯一性，一般作为数据装载（Load）时的关联键；而DESCRIPTION则记录了详细描述信息，在多维展示和分析时我们都会选择使用DESCRIPTION来表述具体含义。这3个属性一般是所有Level都会共用的，而比如用于描述星期几的属性weekid可能只会用于“日期”这层，因为年月都不具备这一信息。所以图中我将Attributes放到了一个层面上，就如同是不同的Level从底层的多个Attributes中选取自身所需的属性，Attributes层是包含着各个Level的共有和特有属性的集合。

Hierarchy

　　因为不知道怎么翻译好，所以还是用英文吧。Hierarchy（等级、层级的意思），中文的OLAP相关文档中普遍翻译为“层次”，而上面的Level被普遍翻译为“级别”，我经常会被这样的翻译搞混淆，所以我上面也一直用Level，至少对我来说这样看起来反而清晰点   。

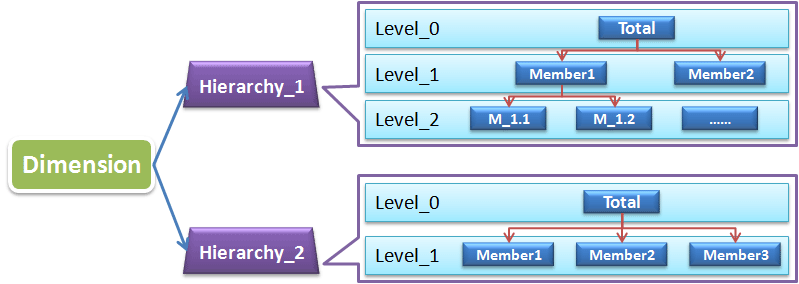
　　因为上面这个结构的维是无法直接应用于OLAP的，我前面的文章有介绍，其实OLAP需要基于有层级的自上而下的钻取，或者自下而上地聚合。所以每一个维必须有Hierarchy，至少有一个默认的，当然可以有多个，见下图：

　　有了Hierarchy，维里面的Level就有了自上而下的树形结构关系，也就是上层的每一个成员（Member）都会包含下层的0个或多个成员，也就是树的分支节点。这里需要注意的是每个Hierarchy树的根节点一般都设置成所有成员的汇总（Total），当该维未被OLAP中使用时，默认显示的就是该维上的汇总节点，也就是该维所有数据的聚合（或者说该维未被用于细分）。Hierarchy中的每一层都会包含若干个成员（Member），还是以时间维，假设我们建的是2006-2015这样一个时间跨度的时间维，那么最高层节点仅有一个Total的成员，包含了所有这10年的时间，而年的那层Level中包含2006、2007…2015这10个成员，每一年又包含了4个季度成员，每个季度包含3个月份成员……这样似乎顺理成章多了，我们就可以基于Hierarchy做一些OLAP操作了。

　　每个Hierarchy都包含了一个树形结构，但维中也可以包含多个Hierarchy，正如上图所示，维中的Hierarchy相互独立地构建了自己的树形结构。还是以时间维为例，时间维可以根据日历（Calendar）时间组建日历的Hierarchy，也可以根据财务（Fiscal）时间组建财务的Hierarchy，而其中财务季度的划分可能并不与日历一致，基于这种多样的Hierarchy，我们在组建多维模型时可以按需选择合适的，比如给财务部的数据分析模型选用财务Hierarchy，而其他部门的分析人员显然希望看到日历样式的Hierarchy，这样就完美地满足了不同的需求。多种的Hierarchy划分同样适用于产品维，根据产品类型、产品规格等划分 Hierarchy，对于按多种条件的产品筛选和检索是十分有效的，实例可以参见淘宝搜索商品界面和太平洋电脑中产品报价界面分类筛选模块，这里不再截图了。

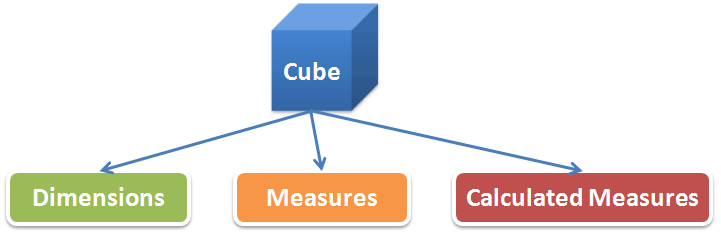
立方（Cube）

　　这里所说的立方其实就是多维模型中间的事实表（Fact Table），它会引用所有相关维的维主键作为自身的联合主键，加上度量（Measure）和计算度量（Calculated Measure）就组成了立方的结构：

　　度量是用于描述事件的数字尺度，比如网站的浏览量（Pageviews）、访问量（Visits），再如电子商务的订单量、销售额等。度量是实际储存于物理表中的，而计算度量则没有，计算度量是通过度量计算得到的，比如同比（如去年同期的月利润）、环比（如上个月的利润）、利率（如环比利润增长率）、份额（如该月中某类产品利润所占比例）、累计（如从年初到当前的累加利润）、移动平均（如最近7天的平均利润额）等，这些计算度量在Oracle中都可以借助分析函数直接计算得到，相信大部分的OLAP组件都会提供类似在时间序列上的分析功能。而这些计算度量往往对于分析而言更具意义，立方中借助与各个维的关联关系从不同的角度和层面来展现这些度量。