1127 ZigZagging on a Tree (30分)

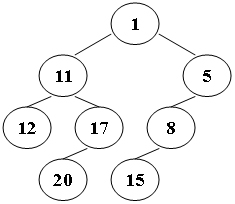
Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences. And it is a simple standard routine to print the numbers in level-order. However, if you think the problem is too simple, then you are too naive. This time you are supposed to print the numbers in "zigzagging order" -- that is, starting from the root, print the numbers level-by-level, alternating between left to right and right to left. For example, for the following tree you must output: 1 11 5 8 17 12 20 15.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the inorder sequence and the third line gives the postorder sequence. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the zigzagging sequence of the tree in a line. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1

 

Sample Output:

1 11 5 8 17 12 20 15

这题考察建树和层序交错打印一棵树，我们只需要在层序遍历的时候进行赋值属于第N层，紧接着进行顺序或者逆序打印即可

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
struct node {
    int data;
    node *left, *right;
    node(int d): data(d), left(NULL), right(NULL) {}
}*root;
int N, in[99999], post[99999], maxLevel = -1;
node* build(int root, int start, int end) {
    if(start > end) return NULL;
    int i = start;
    while(i < end && in[i] != post[root]) i++;
    node *n = new node(in[i]);
    n->left = build(root - 1 - (end - i), start, i - 1);
    n->right = build(root - 1, i + 1, end);
    return n;
}
vector<node*> v[99999], ans;
void level(node *root) {
    queue<pair<node*, int>> que;
    que.push({root, 0});
    while(!que.empty()) {
        pair<node*, int> n = que.front();
        v[n.second].push_back(n.first);
        maxLevel = max(maxLevel, n.second);
        que.pop();
        if(n.first->left) que.push({n.first->left, n.second + 1});
        if(n.first->right) que.push({n.first->right, n.second + 1});
    }
}
int main() {
    scanf("%d", &N);
    for(int i = 0; i < N; i++)
        scanf("%d", &in[i]);
    for(int i = 0; i < N; i++)
        scanf("%d", &post[i]);
    root = build(N - 1, 0, N - 1);
    level(root);
    for(int i = 0; i <= maxLevel; i++) {
        if(i % 2 == 0) {
            for(int j = v[i].size() - 1; j >= 0; j--) 
                ans.push_back(v[i][j]);
        } else {
            for(int j = 0; j < v[i].size(); j++) 
                ans.push_back(v[i][j]);
        }
    }
    printf("%d", ans[0]->data);
    for(int i = 1; i < ans.size(); i++)
        printf(" %d", ans[i]->data);
    return 0;
}