1135 Is It A Red-Black Tree (30分)

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

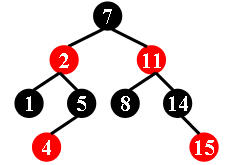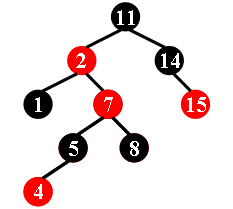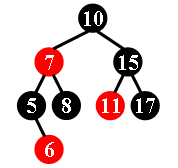Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

 

Sample Output:

Yes
No
No

这道题目考察了红黑树的判断，我们按照二叉树插入顺序，之后判断题目中的5个条件即可

#include <iostream>
using namespace std;
struct node {
    int val;
    node *left, *right;
    node(int v): val(v), left(NULL), right(NULL) {}
};
node* insert(node *n, int v) {
    if(!n) return new node(v);
    else if(abs(n->val) < abs(v)) n->left = insert(n->left, v);
    else n->right = insert(n->right, v);
    return n;
}
bool judge = true; 
int black = -1;
void dfs(node *root, int blacknum) {
    if(!root) {
        if(black == -1) black = blacknum;
        else if(black != blacknum) judge = false;
        return;
    }
    if(root->val > 0) blacknum++;
    if(root->left && root->val < 0 && root->left->val < 0) judge = false;
    if(root->right && root->val < 0 && root->right->val < 0) judge = false;
    dfs(root->left, blacknum);
    dfs(root->right, blacknum);
}
int main() {
    int N, K, v;
    cin >> N;
    while(N--) {
        cin >> K;
        node *root = NULL;
        judge = true;
        black = -1;
        while(K--) {
            cin >> v;
            root = insert(root, v);
        }
        if(root->val < 0) judge = false; 
        dfs(root, 0);
        if(judge) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}