AVL树（C++&Java）

目录

• AVL Tree精讲专题
  • 前言
  • 一、AVL Tree for CPP(Coding)
    • 1.AVL树原型
    • 2.旋转的四种方式
      • • 1.singleLeftRotation LL旋转
        • 2.singleRightRotation RR旋转
        • 3.doubleLeftRightRotation LR旋转
        • 4.doubleRightLeftRotation RL旋转
  • 二、完整版AVL Tree的CPP和JAVA实现
    • AVL Tree CPP FULL Coding
    • AVL Tree JAVA FULL Coding
      • • 1.AVL节点类
        • 2.AVL树类
        • 3.测试用例
        • 4.测试结果截图

AVL Tree精讲专题

前言

因为AVL树之前写过一次，但是感觉左右旋转弄反了，这次重新整理了下，参照数据结构——陈越著，分别进行列举c++版本的AVL树和Java版本的AVL树，供参考和互相学习。图片来源，我们老师的PPT。

一、AVL Tree for CPP(Coding)

1.AVL树原型

C++ coding：

//AVL节点，一个左子树，一个右子树
struct node{
    int val;
    struct node *left,*right;
};

Java coding：

/**
 * AVL节点类
 */
public class AVLNode<T extends Comparable> {
    public T val;
    public AVLNode left;
    public AVLNode right;

    /**
     * constructor
     * @param val
     */
    public AVLNode(T val) {
        this.val = val;
    }
}

2.旋转的四种方式

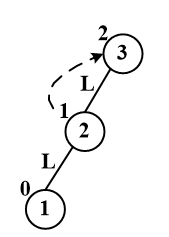
1.singleLeftRotation LL旋转

将3,2节点对换，但是，要注意，2节点右子树可能有其他树

C++ coding：

node *singleLeftRotation(node *root){
    node *t=root->left;
    root->left=t->right;
    t->right=root;
    return t;
}

Java coding：

/**
 * 左单旋
 * @param root
 * @return
 */
public AVLNode singleLeftRotation(AVLNode root){
    AVLNode t=root.left;
    root.left=t.right;
    t.right=root;
    return t;
}

2.singleRightRotation RR旋转

将1,2节点对换，但是，要注意，2节点左子树可能有其他树

C++ coding：

node *singleRightRotation(node *root){
    node *t=root->right;
    root->right=t->left;
    t->left=root;
    return t;
}

Java coding：

/**
 * 右单旋
 * @param root
 * @return
 */
public AVLNode singleRightRotation(AVLNode root){
    AVLNode t=root.right;
    root.right=t.left;
    t.left=root;
    return t;
}

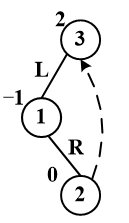
3.doubleLeftRightRotation LR旋转

注意双旋转，先进行下方节点旋转，所以，首先，1,2进行RR旋转，之后对3和3的左子树进行LL旋转。

C++ coding：

node *doubleLeftRightRotation(node *root){
    root->left=singleRightRotation(root->left);
    return singleLeftRotation(root);
}

Java coding：

/**
 * 左右双旋
 * @param root
 * @return
 */
public AVLNode doubleLeftRightRotation(AVLNode root){
    root.left=singleRightRotation(root.left);
    return singleLeftRotation(root);
}

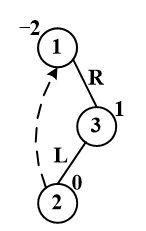
4.doubleRightLeftRotation RL旋转

首先，2,3进行LL旋转，之后对1和1的右子树进行LL旋转。

C++ coding：

node *doubleRightLeftRotation(node *root){
    root->right=singleLeftRotation(root->right);
    return singleRightRotation(root);
}

Java coding：

/**
 * 右左双旋
 * @param root
 * @return
 */
public AVLNode doubleRightLeftRotation(AVLNode root){
    root.right=singleLeftRotation(root.right);
    return singleRightRotation(root);
}

插入代码

我们插入时，首先判断是否是空树，是空树就进行填充。之后进行左右递归插入（与BST树插入效果一样），紧接着我们需要进行一次判断，在左侧插入时，如果插入值比左孩子值还要小，那么，是LL了，进行LL旋转，如果比左孩子值大，那么进行LR旋转。右侧插入同理。

C++ coding：

node *insert(node *root,int val){
    if(root==NULL){
        root=new node();
        root->val=val;
        root->left=NULL;
        root->right=NULL;
    }else if(val<root->val){
        root->left=insert(root->left,val);
        if(getHeight(root->left)-getHeight(root->right)==2)
            root=val<root->left->val ? singleLeftRotation(root):doubleLeftRightRotation(root);
    }else{
        root->right=insert(root->right,val);
        if(getHeight(root->left)-getHeight(root->right)==-2)
            root=val>root->right->val ? singleRightRotation(root):doubleRightLeftRotation(root);
    }
    return root;
}

Java coding：

/**
 * 插入方法
 * @param val 插入变量
 */
public void insert(T val){
    root=insert(root,val);
}

/**
 * 插入辅助方法
 * @param root
 * @param val
 * @return
 */
private AVLNode<T> insert(AVLNode root, T val) {
    if(root==null){
        //空树插入
        root=new AVLNode(val);
    }else if(val.compareTo(root.val)<0){
        //小于根进行左插入
        root.left=insert(root.left,val);
        //旋转操作
        if((getHeight(root.left)-getHeight(root.right))==2){
            root=val.compareTo(root.left.val)<0 ? singleLeftRotation(root):doubleLeftRightRotation(root);
        }
    }else{
        //大于根进行右插入
        root.right=insert(root.right,val);
        //旋转操作
        if((getHeight(root.left)-getHeight(root.right))==-2) {
            root = val.compareTo(root.right.val) > 0 ? singleRightRotation(root) : doubleRightLeftRotation(root);
        }
    }
    return root;
}

二、完整版AVL Tree的CPP和JAVA实现

AVL Tree CPP FULL Coding

这边加入了先序遍历和高度检测，代码可直接运行。

#include <iostream>

using namespace std;

struct node{
    int val;
    struct node *left,*right;
};

node *singleLeftRotation(node *root){
    node *t=root->left;
    root->left=t->right;
    t->right=root;
    return t;
}

node *singleRightRotation(node *root){
    node *t=root->right;
    root->right=t->left;
    t->left=root;
    return t;
}

node *doubleLeftRightRotation(node *root){
    root->left=singleRightRotation(root->left);
    return singleLeftRotation(root);
}

node *doubleRightLeftRotation(node *root){
    root->right=singleLeftRotation(root->right);
    return singleRightRotation(root);
}

int getHeight(node *root){
    if(root==NULL) return 0;
    return max(getHeight(root->left),getHeight(root->right))+1;
}

node *insert(node *root,int val){
    if(root==NULL){
        root=new node();
        root->val=val;
        root->left=NULL;
        root->right=NULL;
    }else if(val<root->val){
        root->left=insert(root->left,val);
        if(getHeight(root->left)-getHeight(root->right)==2)
            root=val<root->left->val ? singleLeftRotation(root):doubleLeftRightRotation(root);
    }else{
        root->right=insert(root->right,val);
        if(getHeight(root->left)-getHeight(root->right)==-2)
            root=val>root->right->val ? singleRightRotation(root):doubleRightLeftRotation(root);
    }
    return root;
}

void preOrder(node *root){
    if(root==NULL) return;
    printf("%d ",root->val);
    preOrder(root->left);
    preOrder(root->right);
}
int main(){
    int n,val;
    scanf("%d",&n);
    node *root=NULL;
    for(int i=0;i<n;i++){
        scanf("%d",&val);
        root=insert(root,val);
    }
    preOrder(root);
    system("pause");
    return 0;
}

AVL Tree JAVA FULL Coding

1.AVL节点类

package test;

/**
 * AVL节点类
 */
public class AVLNode<T extends Comparable> {
    public T val;
    public AVLNode left;
    public AVLNode right;

    /**
     * constructor
     * @param val
     */
    public AVLNode(T val) {
        this.val = val;
    }
}

2.AVL树类

package test;

/**
 * AVL Tree类
 * 维持平衡的AVL树
 * @param <T>
 */
public class AVLTree<T extends Comparable> {

    public AVLNode<T> root;

/**
 * 插入方法
 * @param val 插入变量
 */
public void insert(T val){
    root=insert(root,val);
}

/**
 * 插入辅助方法
 * @param root
 * @param val
 * @return
 */
private AVLNode<T> insert(AVLNode root, T val) {
    if(root==null){
        //空树插入
        root=new AVLNode(val);
    }else if(val.compareTo(root.val)<0){
        //小于根进行左插入
        root.left=insert(root.left,val);
        //旋转操作
        if((getHeight(root.left)-getHeight(root.right))==2){
            root=val.compareTo(root.left.val)<0 ? singleLeftRotation(root):doubleLeftRightRotation(root);
        }
    }else{
        //大于根进行右插入
        root.right=insert(root.right,val);
        //旋转操作
        if((getHeight(root.left)-getHeight(root.right))==-2) {
            root = val.compareTo(root.right.val) > 0 ? singleRightRotation(root) : doubleRightLeftRotation(root);
        }
    }
    return root;
}

    /**
     * 左单旋
     * @param root
     * @return
     */
    public AVLNode singleLeftRotation(AVLNode root){
        AVLNode t=root.left;
        root.left=t.right;
        t.right=root;
        return t;
    }

    /**
     * 右单旋
     * @param root
     * @return
     */
    public AVLNode singleRightRotation(AVLNode root){
        AVLNode t=root.right;
        root.right=t.left;
        t.left=root;
        return t;
    }

    /**
     * 左右双旋
     * @param root
     * @return
     */
    public AVLNode doubleLeftRightRotation(AVLNode root){
        root.left=singleRightRotation(root.left);
        return singleLeftRotation(root);
    }

    /**
     * 右左双旋
     * @param root
     * @return
     */
    public AVLNode doubleRightLeftRotation(AVLNode root){
        root.right=singleLeftRotation(root.right);
        return singleRightRotation(root);
    }

    /**
     * 获取树的高度
     * @param root 传入根节点
     * @return
     */
    private int getHeight(AVLNode root){
        if(root==null) {
            return 0;
        }
        return (getHeight(root.left)>getHeight(root.right) ? getHeight(root.left):getHeight(root.right))+1;
    }

    /**
     * 先序遍历
     */
    public void preOrderTraserve(){
        preOrderTraserve(root);
    }

    /**
     * 先序遍历辅助方法
     * @param root
     */
    public void preOrderTraserve(AVLNode root){
        if(root==null){
            return;
        }
        System.out.print(root.val+" ");
        preOrderTraserve(root.left);
        preOrderTraserve(root.right);
    }
}

3.测试用例

package test;

import java.util.Scanner;

public class TestDemo {
    public static void main(String[] args) {
        AVLTree<Integer> avlTree=new AVLTree();
        Scanner sc=new Scanner(System.in);
        System.out.println("输入你要插入节点个数：");
        int num=sc.nextInt();int tmp;
        while(num--!=0){
            tmp=sc.nextInt();
            avlTree.insert(tmp);
        }
        avlTree.preOrderTraserve();
        sc.close();
    }
}

4.测试结果截图