【转载】马尔科夫决策过程简要介绍
一篇不错的介绍马尔科夫过程的文章,原文地址(http://www.cnblogs.com/jerrylead/archive/2011/05/13/2045309.html)
在之前的讨论中,我们总是给定一个样本x,然后给或者不给label y。之后对样本进行拟合、分类、聚类或者降维等操作。然而对于很多序列决策或者控制问题,很难有这么规则的样本。比如,四足机器人的控制问题,刚开始都不知道应该让其动那条腿,在移动过程中,也不知道怎么让机器人自动找到合适的前进方向。
另外如要设计一个下象棋的AI,每走一步实际上也是一个决策过程,虽然对于简单的棋有A*的启发式方法,但在局势复杂时,仍然要让机器向后面多考虑几步后才能决定走哪一步比较好,因此需要更好的决策方法。
对于这种控制决策问题,有这么一种解决思路。我们设计一个回报函数(reward function),如果learning agent(如上面的四足机器人、象棋AI程序)在决定一步后,获得了较好的结果,那么我们给agent一些回报(比如回报函数结果为正),得到较差的结果,那么回报函数为负。比如,四足机器人,如果他向前走了一步(接近目标),那么回报函数为正,后退为负。如果我们能够对每一步进行评价,得到相应的回报函数,那么就好办了,我们只需要找到一条回报值最大的路径(每步的回报之和最大),就认为是最佳的路径。
增强学习在很多领域已经获得成功应用,比如自动直升机,机器人控制,手机网络路由,市场决策,工业控制,高效网页索引等。
接下来,先介绍一下马尔科夫决策过程(MDP,Markov decision processes)。
1. 马尔科夫决策过程
* S表示状态集(states)。(比如,在自动直升机系统中,直升机当前位置坐标组成状态集)
* A表示一组动作(actions)。(比如,使用控制杆操纵的直升机飞行方向,让其向前,向后等)
* ![]() 是状态转移概率。S中的一个状态到另一个状态的转变,需要A来参与。
是状态转移概率。S中的一个状态到另一个状态的转变,需要A来参与。![]() 表示的是在当前
表示的是在当前![]() 状态下,经过
状态下,经过![]() 作用后,会转移到的其他状态的概率分布情况(当前状态执行a后可能跳转到很多状态)。
作用后,会转移到的其他状态的概率分布情况(当前状态执行a后可能跳转到很多状态)。
* ![]() ,R是回报函数(reward function),回报函数经常写作S的函数(只与S有关),这样的话,R重新写作
,R是回报函数(reward function),回报函数经常写作S的函数(只与S有关),这样的话,R重新写作![]() 。
。
MDP的动态过程如下:某个agent的初始状态为![]() ,然后从A中挑选一个动作
,然后从A中挑选一个动作![]() 执行,执行后,agent按
执行,执行后,agent按![]() 概率随机转移到了下一个
概率随机转移到了下一个![]() 状态,
状态,![]() 。然后再执行一个动作
。然后再执行一个动作![]() ,就转移到了
,就转移到了![]() ,接下来再执行
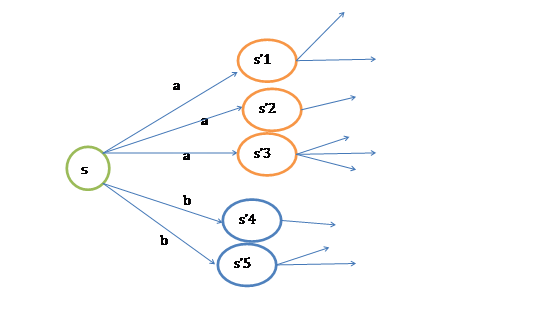
,接下来再执行![]() …,我们可以用下面的图表示整个过程
…,我们可以用下面的图表示整个过程
如果对HMM有了解的话,理解起来比较轻松。
我们定义经过上面转移路径后,得到的回报函数之和如下
如果R只和S有关,那么上式可以写作
我们的目标是选择一组最佳的action,使得全部的回报加权和期望最大。
从上式可以发现,在t时刻的回报值被打了![]() 的折扣,是一个逐步衰减的过程,越靠后的状态对回报和影响越小。最大化期望值也就是要将大的
的折扣,是一个逐步衰减的过程,越靠后的状态对回报和影响越小。最大化期望值也就是要将大的![]() 尽量放到前面,小的尽量放到后面。
尽量放到前面,小的尽量放到后面。
已经处于某个状态s时,我们会以一定策略![]() 来选择下一个动作a执行,然后转换到另一个状态s’。我们将这个动作的选择过程称为策略(policy),每一个policy其实就是一个状态到动作的映射函数
来选择下一个动作a执行,然后转换到另一个状态s’。我们将这个动作的选择过程称为策略(policy),每一个policy其实就是一个状态到动作的映射函数![]() 。给定
。给定![]() 也就给定了
也就给定了![]() ,也就是说,知道了
,也就是说,知道了![]() 就知道了每个状态下一步应该执行的动作。
就知道了每个状态下一步应该执行的动作。
我们为了区分不同![]() 的好坏,并定义在当前状态下,执行某个策略
的好坏,并定义在当前状态下,执行某个策略![]() 后,出现的结果的好坏,需要定义值函数(value function)也叫折算累积回报(discounted cumulative reward)
后,出现的结果的好坏,需要定义值函数(value function)也叫折算累积回报(discounted cumulative reward)
可以看到,在当前状态s下,选择好policy后,值函数是回报加权和期望。这个其实很容易理解,给定![]() 也就给定了一条未来的行动方案,这个行动方案会经过一个个的状态,而到达每个状态都会有一定回报值,距离当前状态越近的其他状态对方案的影响越大,权重越高。这和下象棋差不多,在当前棋局
也就给定了一条未来的行动方案,这个行动方案会经过一个个的状态,而到达每个状态都会有一定回报值,距离当前状态越近的其他状态对方案的影响越大,权重越高。这和下象棋差不多,在当前棋局![]() 下,不同的走子方案是
下,不同的走子方案是![]() ,我们评价每个方案依靠对未来局势(
,我们评价每个方案依靠对未来局势(![]() ,
,![]() ,…)的判断。一般情况下,我们会在头脑中多考虑几步,但是我们会更看重下一步的局势。
,…)的判断。一般情况下,我们会在头脑中多考虑几步,但是我们会更看重下一步的局势。
从递推的角度上考虑,当期状态s的值函数V,其实可以看作是当前状态的回报R(s)和下一状态的值函数V’之和,也就是将上式变为:
然而,我们需要注意的是虽然给定![]() 后,在给定状态s下,a是唯一的,但
后,在给定状态s下,a是唯一的,但![]() 可能不是多到一的映射。比如你选择a为向前投掷一个骰子,那么下一个状态可能有6种。再由Bellman等式,从上式得到
可能不是多到一的映射。比如你选择a为向前投掷一个骰子,那么下一个状态可能有6种。再由Bellman等式,从上式得到
s’表示下一个状态。
前面的R(s)称为立即回报(immediate reward),就是R(当前状态)。第二项也可以写作![]() ,是下一状态值函数的期望值,下一状态s’符合
,是下一状态值函数的期望值,下一状态s’符合![]() 分布。
分布。
可以想象,当状态个数有限时,我们可以通过上式来求出每一个s的V(终结状态没有第二项V(s’))。如果列出线性方程组的话,也就是|S|个方程,|S|个未知数,直接求解即可。
当然,我们求V的目的就是想找到一个当前状态s下,最优的行动策略![]() ,定义最优的V*如下:
,定义最优的V*如下:
就是从可选的策略![]() 中挑选一个最优的策略(discounted rewards最大)。
中挑选一个最优的策略(discounted rewards最大)。
上式的Bellman等式形式如下:
第一项与![]() 无关,所以不变。第二项是一个
无关,所以不变。第二项是一个![]() 就决定了每个状态s的下一步动作a,执行a后,s’按概率分布的回报概率和的期望。
就决定了每个状态s的下一步动作a,执行a后,s’按概率分布的回报概率和的期望。
如果上式还不好理解的话,可以参考下图:
根据以上式子,我们可以知道
解释一下就是当前状态的最优的值函数V*,是由采用最优执行策略![]() 的情况下得出的,采用最优执行方案的回报显然要比采用其他的执行策略
的情况下得出的,采用最优执行方案的回报显然要比采用其他的执行策略![]() 要好。
要好。
这里需要注意的是,如果我们能够求得每个s下最优的a,那么从全局来看,![]() 的映射即可生成,而生成的这个映射是最优映射,称为
的映射即可生成,而生成的这个映射是最优映射,称为![]() 。
。![]() 针对全局的s,确定了每一个s的下一个行动a,不会因为初始状态s选取的不同而不同。
针对全局的s,确定了每一个s的下一个行动a,不会因为初始状态s选取的不同而不同。
2. 值迭代和策略迭代法
上节我们给出了迭代公式和优化目标,这节讨论两种求解有限状态MDP具体策略的有效算法。这里,我们只针对MDP是有限状态、有限动作的情况,![]() 。
。
* 值迭代法
|
1、 将每一个s的V(s)初始化为0 2、 循环直到收敛 { 对于每一个状态s,对V(s)做更新 } |
值迭代策略利用了上节中公式(2)
内循环的实现有两种策略:
1、 同步迭代法
拿初始化后的第一次迭代来说吧,初始状态所有的V(s)都为0。然后对所有的s都计算新的V(s)=R(s)+0=R(s)。在计算每一个状态时,得到新的V(s)后,先存下来,不立即更新。待所有的s的新值V(s)都计算完毕后,再统一更新。
这样,第一次迭代后,V(s)=R(s)。
2、 异步迭代法
与同步迭代对应的就是异步迭代了,对每一个状态s,得到新的V(s)后,不存储,直接更新。这样,第一次迭代后,大部分V(s)>R(s)。
不管使用这两种的哪一种,最终V(s)会收敛到V*(s)。知道了V*后,我们再使用公式(3)来求出相应的最优策略![]() ,当然
,当然![]() 可以在求V*的过程中求出。
可以在求V*的过程中求出。
* 策略迭代法
|
2、 循环直到收敛 { } |
(a)步中的V可以通过之前的Bellman等式求得
(b)步实际上就是根据(a)步的结果挑选出当前状态s下,最优的a,然后对![]() 做更新。
做更新。
对于值迭代和策略迭代很难说哪种方法好,哪种不好。对于规模比较小的MDP来说,策略一般能够更快地收敛。但是对于规模很大(状态很多)的MDP来说,值迭代比较容易(不用求线性方程组)。
3. MDP中的参数估计
在之前讨论的MDP中,我们是已知状态转移概率![]() 和回报函数R(s)的。但在很多实际问题中,这些参数不能显式得到,我们需要从数据中估计出这些参数(通常S、A和
和回报函数R(s)的。但在很多实际问题中,这些参数不能显式得到,我们需要从数据中估计出这些参数(通常S、A和![]() 是已知的)。
是已知的)。
假设我们已知很多条状态转移路径如下:
其中,![]() 是i时刻,第j条转移路径对应的状态,
是i时刻,第j条转移路径对应的状态,![]() 是
是![]() 状态时要执行的动作。每个转移路径中状态数是有限的,在实际操作过程中,每个转移链要么进入终结状态,要么达到规定的步数就会终结。
状态时要执行的动作。每个转移路径中状态数是有限的,在实际操作过程中,每个转移链要么进入终结状态,要么达到规定的步数就会终结。
如果我们获得了很多上面类似的转移链(相当于有了样本),那么我们就可以使用最大似然估计来估计状态转移概率。
分子是从s状态执行动作a后到达s’的次数,分母是在状态s时,执行a的次数。两者相除就是在s状态下执行a后,会转移到s’的概率。
为了避免分母为0的情况,我们需要做平滑。如果分母为0,则令![]() ,也就是说当样本中没有出现过在s状态下执行a的样例时,我们认为转移概率均分。
,也就是说当样本中没有出现过在s状态下执行a的样例时,我们认为转移概率均分。
上面这种估计方法是从历史数据中估计,这个公式同样适用于在线更新。比如我们新得到了一些转移路径,那么对上面的公式进行分子分母的修正(加上新得到的count)即可。修正过后,转移概率有所改变,按照改变后的概率,可能出现更多的新的转移路径,这样![]() 会越来越准。
会越来越准。
同样,如果回报函数未知,那么我们认为R(s)为在s状态下已经观测到的回报均值。
当转移概率和回报函数估计出之后,我们可以使用值迭代或者策略迭代来解决MDP问题。比如,我们将参数估计和值迭代结合起来(在不知道状态转移概率情况下)的流程如下:
|
2、 循环直到收敛 { (b) 使用估计到的参数来更新V(使用上节的值迭代方法) } |
在(b)步中我们要做值更新,也是一个循环迭代的过程,在上节中,我们通过将V初始化为0,然后进行迭代来求解V。嵌套到上面的过程后,如果每次初始化V为0,然后迭代更新,就会很慢。一个加快速度的方法是每次将V初始化为上一次大循环中得到的V。也就是说V的初值衔接了上次的结果。
4. 总结
首先我们这里讨论的MDP是非确定的马尔科夫决策过程,也就是回报函数和动作转换函数是有概率的。在状态s下,采取动作a后的转移到的下一状态s’也是有概率的。再次,在增强学习里有一个重要的概念是Q学习,本质是将与状态s有关的V(s)转换为与a有关的Q。强烈推荐Tom Mitchell的《机器学习》最后一章,里面介绍了Q学习和更多的内容。最后,里面提到了Bellman等式,在《算法导论》中有Bellman-Ford的动态规划算法,可以用来求解带负权重的图的最短路径,里面最值得探讨的是收敛性的证明,非常有价值。有学者仔细分析了增强学习和动态规划的关系。

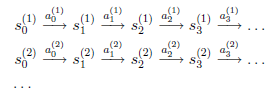


 浙公网安备 33010602011771号
浙公网安备 33010602011771号