[CF700E](Cool Slogans)

QY 大神仙：这就是SAM大水题，快切快切

然而还没怎么理解SAM的我表示对着题解一脸懵逼

设原串为s；

对于后缀自动机上的一个点i,定义dp[i]为点i表示的字符串的答案（最长嵌套次数）

显然点i应从fa[i],fa[fa[i]]等endpos包含endpos(i)的节点转移过来，为什么呢？

因为后缀自动机的性质，fa[i]所代表的字符串都是i所代表的字符串的后缀（endpos），如果答案（嵌套的字符串）不包含s[endpos(i)]的话，就不用i去更新。

举个栗子(from here)

 

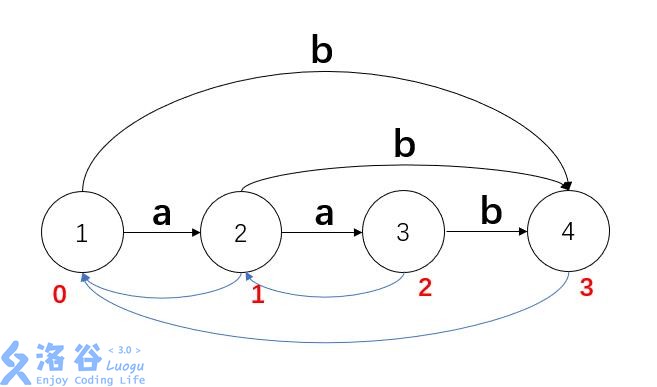
这里的4号节点，也就是（len最长的字符串）aab,它的father是1，也就是意味着它的答案没法更新（dp[4]=1）

可是aab里面有两个a，理论上答案是2，但因为3号节点（也就是aa）已经能通过fa[3]=2号节点来转移达到dp[3]=2;

所以4号节点需要管的转移只有它的后缀，也就是它的fa所包含的字符，真的只是fa[i]吗？注意到其实是fa[i],fa[fa[i]],fa[fa[fa[i]]]等fa树上一路跳上去的节点

好，那么我们得出（其实都是博主在瞎扯）点i只需从fa[i],fa[fa[i]]等节点转移过来，

由于字符串i嵌套字符串fa[i]肯定比嵌套字符串fa[fa[i]]难，所以我们记top[i]为i的fa树路径上最浅的dp值等于dp[i]的位置，也就是说从top[i]到i都没有嵌套来更新dp值

那么i就可以从top[fa]转移过来而不是从fa树上一路跳上去更新

那么还剩下具体的更新部分，也就是怎么判节点top[fa[a]]代表的字符串在节点a代表的字符串中出现了两次呢？

这里我们用endpos来判断,如果top[fa[a]]的至少两个endpos在a代表的最长字符串所覆盖的区间里出现过就成立

因为top[fa[a]]是a的后缀，所以肯定已经出现了一次，所以只要在（pos[a]-len[a]+len[top[fa[a]]],pos[a]-1）中出现过一次即可

等等，这是什么式子？

这里 pos[a]为a代表的最长字符串的最后一个字符在原串s中的位置，len[a]为a代表的最长字符串的长度

那么pos[a]-len[a]+1 到pos[a]即a代表的最长字符串所覆盖的区间，当然top[fa[a]]的endpos当然是不能在区间前len[top[fa[a]]-1的点出现的，不然还是越界

又因为top[fa[a]]的endpos在pos[a]肯定出现过一次所以要把这个点舍掉，那么这就是整个式子了

至于怎么维护一个节点的endpos集合，线段树合并即可。

(扯完了，上code):

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define N 400004
#define mid (l+r>>1)
using namespace std;
struct seg {
    int L[N*20],R[N*20],tot;
    void init() {
        tot=0;
        }
    void insert(int &now,int l,int r,int pos) {
        if(!now)now=++tot;
        if(l==r)return;
        if(pos<=mid)insert(L[now],l,mid,pos);
        else insert(R[now],mid+1,r,pos);
        }
    int merge(int A,int B) {
        if(!A||!B)return A+B;
        int it=++tot;
        L[it]=merge(L[A],L[B]);
        R[it]=merge(R[A],R[B]);
        return it;
        }
    int query(int now,int l,int r,int nl,int nr) {
        if(!now)return 0;
        if(nl<=l&&r<=nr)return 1;
        if(nl<=mid&&query(L[now],l,mid,nl,nr))return 1;
        if(mid<nr&&query(R[now],mid+1,r,nl,nr))return 1;
        return 0;
        }
    } aux;
int rt[N];
struct SAM {
    int cnt,las;
    int len[N],fa[N],ch[N][26],pos[N];
    void init() {
        cnt=las=1;
        }
    void add(int c,int pi) {
        int p=las,it=las=++cnt;
        len[it]=len[p]+1,pos[it]=pi;
        for(; p&&!ch[p][c]; p=fa[p])ch[p][c]=it;
        if(!p)fa[it]=1;
        else {
            int q=ch[p][c];
            if(len[q]==len[p]+1)fa[it]=q;
            else {
                int np=++cnt;
                for(int i=0; i<26; i++)ch[np][i]=ch[q][i];
                len[np]=len[p]+1,pos[np]=pos[q];
                fa[np]=fa[q],fa[q]=fa[it]=np;
                for(; p&&ch[p][c]==q; p=fa[p])ch[p][c]=np;
                }
            }
        }
    } sett;
void init() {
    sett.init(),aux.init();
    }
int n,tax[N],poi[N];
int dp[N],top[N];
char op[N];
int ans=1;
int main() {
    init();
    scanf("%d",&n);
    scanf("%s",op+1);
    for(int i=1; i<=n; i++) sett.add(op[i]-'a',i),aux.insert(rt[sett.las],1,n,i);
    for(int i=1; i<=sett.cnt; i++)tax[sett.len[i]]++;
    for(int i=1; i<=n; i++)tax[i]+=tax[i-1];
    for(int i=sett.cnt; i>=1; i--)poi[tax[sett.len[i]]--]=i;
    for(int i=sett.cnt; i>1; i--)
      rt[sett.fa[poi[i]]]=aux.merge(rt[sett.fa[poi[i]]],rt[poi[i]]);
    for(int i=2; i<=sett.cnt; i++) {
        int u=poi[i],ff=sett.fa[u];
        if(ff==1)dp[u]=1,top[u]=u;
        else {
            if(aux.query(rt[top[ff]],1,n,sett.pos[u]-sett.len[u]+sett.len[top[ff]],sett.pos[u]-1))
                dp[u]=dp[ff]+1,top[u]=u,ans=max(ans,dp[u]);
            else dp[u]=dp[ff],top[u]=top[ff];
            }
        }
    printf("%d\n",ans);
    }

//syktxdy
//qy dashenxian
//chc duliu