HDU 1710 Binary Tree Traversals
Binary Tree Traversals
Time Limit : 1000/1000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other)
Total Submission(s) : 42 Accepted Submission(s) : 30
Font: Times New Roman | Verdana | Georgia
Font Size: ← →
Problem Description
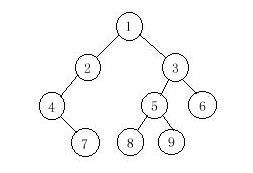
A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.
In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.
In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.
Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.
![]()
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.
In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.
In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.
Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.
Input
The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.
Output
For each test case print a single line specifying the corresponding postorder sequence.
Sample Input
9 1 2 4 7 3 5 8 9 6 4 7 2 1 8 5 9 3 6
Sample Output
7 4 2 8 9 5 6 3 1
Source
HDU 2007-Spring Programming Contest
#include <iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int i,n,len;
int a[1005],b[1005],ans[1005];
struct
{
int num,left,right;
}tree[1005];
int findroot(int root,int l,int r)
{
for(int i=l;i<=r;i++)
if (b[i]==a[root]) return i;
}
void work(int root,int l,int r)
{
if (l>=r) return;
int k=findroot(root,l,r);
if (l<=k-1)
{
tree[++len].num=a[root+1];
tree[root].left=len;
work(root+1,l,k-1);
}
if (k+1<=r)
{
tree[++len].num=a[root+1+k-l];
tree[root].right=len;
work(root+1+k-l,k+1,r);
}
return;
}
void solve(int k)
{
if(tree[k].left!=-1) solve(tree[k].left);
if(tree[k].right!=-1) solve(tree[k].right);
ans[++len]=tree[k].num;
}
int main()
{
while(~scanf("%d",&n))
{
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
for(i=1;i<=n;i++)
scanf("%d",&b[i]);
memset(ans,0,sizeof(ans));
for(i=1;i<=1000;i++)
{
tree[i].num=-1;
tree[i].left=-1;
tree[i].right=-1;
}
len=1;
tree[1].num=a[1];
work(1,1,n);
len=0;
solve(1);
for(i=1;i<n;i++)
printf("%d ",ans[i]);
printf("%d\n",ans[n]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号