787. K 站中转内最便宜的航班 力扣（中等） 动态规划/Bellman Ford/bfs 不会做

787. K 站中转内最便宜的航班

有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。 如果不存在这样的路线，则输出 -1。

示例 1：

输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释:
城市航班图如下

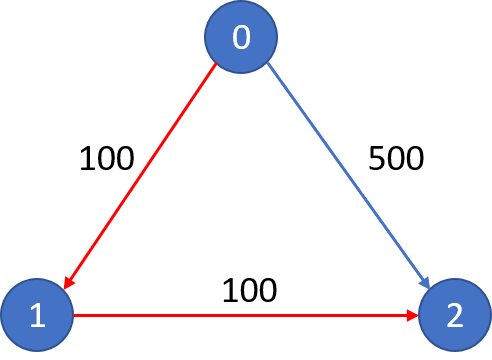
从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200，如图中红色所示。

 

 

 

代码： 动态规划，但我感觉就是bellman ford方法

class Solution {
public:

    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
     int dp[105][105];  // dp[i][j]表示走i步(i-1次中转)，到达j的最短路径
     memset(dp,-1,sizeof(dp));
     dp[0][src]=0;     //  没有中转，首站src
     for(int ti=1;ti<=k+1;ti++)
     {
         for(auto flight:flights)
         {
             int s=flight[0];
             int t=flight[1];
             int c=flight[2];
             if(dp[ti-1][s]!=-1)    // 如果起点站已可达，可以基于此优化
             {
                 if(dp[ti][t]==-1) dp[ti][t]=dp[ti-1][s]+c;  //  还没叨叨过
                    else dp[ti][t]=min(dp[ti][t],dp[ti-1][s]+c);  //  取最优
             }
         }
     }
     int res=0x7fffffff;
     for(int i=1;i<=k+1;i++) 
      if (dp[i][dst]!=-1) res=min(res,dp[i][dst]);  // 所有可能的中转次数
     
     if (res==0x7fffffff) return -1;
     return res;
    }
};