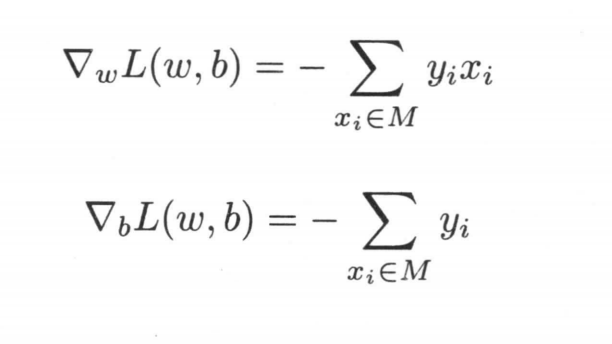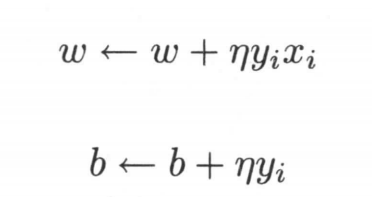机器学习模型之感知机

目录

• 1、感知机模型
• 2、感知机策略
• 3、感知机算法

1、感知机模型

感知机是一个线性分类器，感知机的公式是

\[ f(x) = sign(wx+b) \]

其中

\[ \operatorname{sign}(x)=\left\{\begin{array}{ll} +1, & x \geqslant 0 \\ -1, & x<0 \end{array}\right. \]

感知机说得是我们有一系列的点x = (x1,x2,x3...xn)和相应的参数w = (w1,w2,w3....wn),我们将x和w向量进行乘积操作，最终会得到一个数字，如果这个数字大于等于0，那么我们将其归为+1类别，否则，归为-1类别。

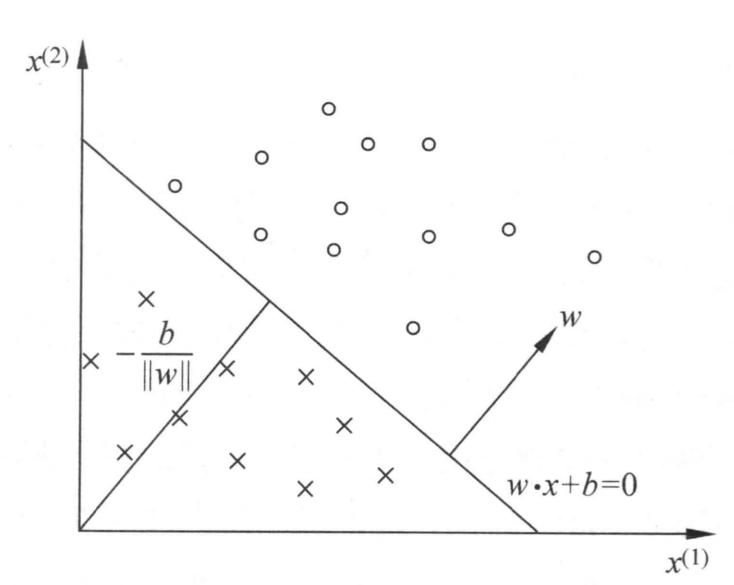
关于\(wx+b\)可以理解为一个超平面，展开就是\(w_{1} x_{1} + w_{2}x_{2} +w_{3}x_{3} + ...... +b\)，当\(wx+b = 0\)时，其表示的就是一个超平面，在二维空间如下图所示

当我们输入一个序列，如果$wx+b>0$那么其也就显示在直线的上方，若$wx+b<0$那就是在直线的下方，若$wx+b=0$则刚好是在直线上。我们发现，对于$wx+b=0$来说，当成倍的扩大w和b，这个直线是没有任何变化的，对于分类结果也不会有任何变化，该分成正类还是正类，该分成负类还是负类。

2、感知机策略

那么我们如何学习感知机的参数w呢？我们的策略就是构建损失函数，那么如何构建损失函数呢？我们想到的一种方法是误分类点的个数作为损失函数，但是这种方法的结果对w和b不可导，那么，我们就想出了另外一种策略，对于误分类的数据，其有一个性质

\[ -y_{i} (wx_{i} + b) > 0 \]

当\(y_{i} = +1，wx_{i} + b = -1\)时，\(-y_{i} (wx_{i} + b) > 0\),当\(y_{i} = -1，wx_{i} + b = +1\)时，\(-y_{i} (wx_{i} + b) > 0\)，那对于分类正确的点怎么办呢？很简单，我们就不管他就行，或者他们的损失就是0，我们加上0就可以了。所以我们的损失函数就是所有误分类点的集合，如下面公式所示

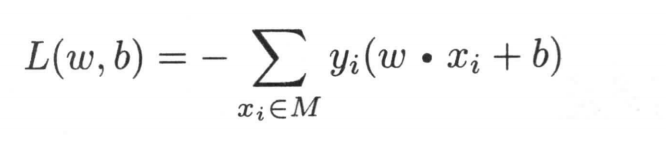
3、感知机算法

那我们如何来求解w和b呢，常用的策略就是对相应的参数进行求导，利用梯度下降法更新参数，求导结果为

参数更新为