RNN和LSTM模型详解

目录

• RNN
  • 为什么会出现RNN
  • RNN模型架构
  • 多输入单输出
  • 单输入多输出
  • 多输入多输出
  • 梯度消失和梯度爆炸
• LSTM
  • 为什么会出现LSTM呢？
  • LSTM模型结构

本文介绍RNN模型和LSTM模型。

RNN

为什么会出现RNN

在传统的深度神经网络模型中，我们的输入信息是没有顺序的，比如，NLP领域中，我们输入单词经常使用embedding，将词汇映射为词向量，然后输入到神经网络。但是这种输入方式会有一些问题，比如，"我 爱 你"和"你 爱 我"在传统的神经网络中不能很好的识别。在这种情况下，有人提出了将n-gram信息加入到输入层，比如fasttext，这样，在一定程度上解决了单词间的顺序问题，但是这种方法也有一些弊端，就是我们无法捕获长句子的单词依赖，比如一个句子n个单词，那么如果想要捕获全部的单词顺序信息，需要1+2+3....+n，所以这种方式会让embedding_lookup变得非常大。

那么，RNN就是专门解决这种无法捕获长距离的句子信息的模型。

RNN模型架构

RNN模型如下图所示，在每一步，我们都输入单词\(w_{i}\)同时，经过公式\(h_{i+1} = sigmoid(W * h_{i} + U *x_{i} + b)\)这里，\(x_{i}\)表示在第\(i\)步输入的单词，\(h_{i}\)表示当前的隐藏层权值向量，\(h_{i+1}\)表示输出。

多输入单输出

接下来介绍几种RNN的使用形式，这些使用形式可以用在不同的场景中。

多输入单输出的形式基本上就是基本模型的一点点扩展，就是我们只用最后一个时间点的输出，在最后一层输出中加入一个softmax。

单输入多输出

单输入多输出是只在第一层输入一次，后续不需要在输入任何的东西，即除了第一层，后续几层的\(U * x_{i}\) 为0.

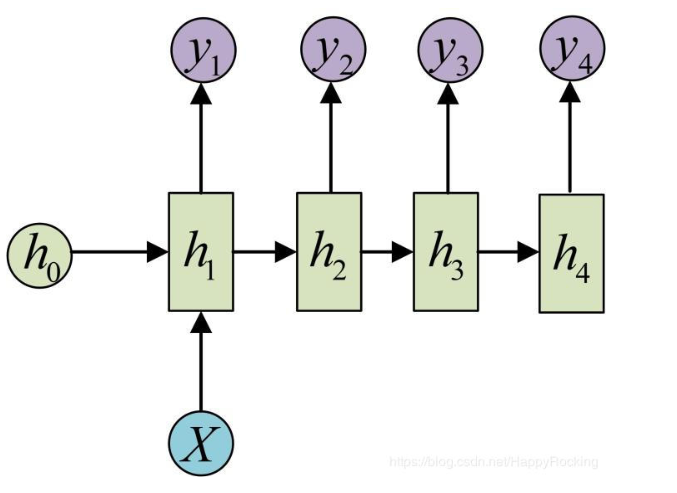
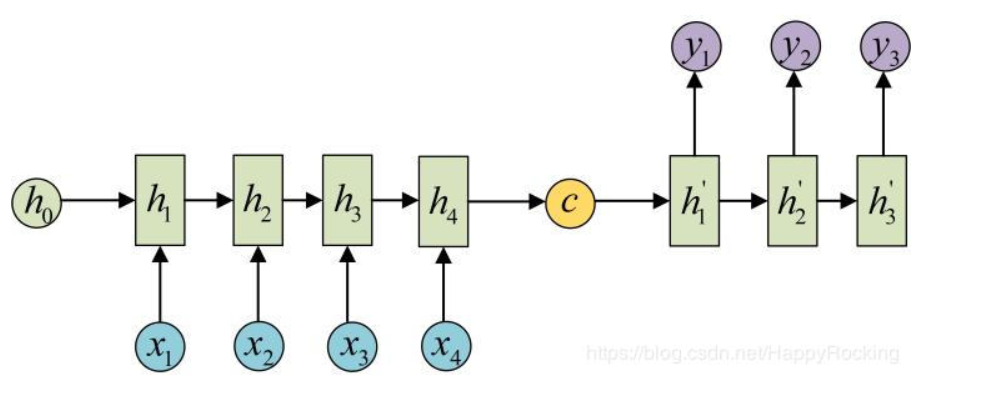
多输入多输出

多输入多输出也可以叫做encoder-decoder模型，常用于翻译。

梯度消失和梯度爆炸

RNN受限于梯度消失和梯度爆炸，为什么会出现这种现象呢？我们借鉴邱锡鹏老师的深度学习和神经网络，来简单的进行一下相关公式的推导，当得到推导结果的时候，我们就能很好的理解为啥会有这种现象了。首先，我们来定义一下RNN的公式

\[h_{t} = f(z_{t}) \\ z_{t} = U * h_{t-1} + W * x_{t} + b \\ \]

上面的公式是RNN的标准公式，其中\(U,W,b\)为需要求的参数，\(h_{t-1}\)为\(t-1\)时刻的输出值，我们假定序列的长度为\(T\)，即\(t=1,2,3,4.....T\),在\(T\)时刻输出的时候，我们定义一个损失函数

\[L = loss(y,h_{T}) \]

这里\(y\)表示标签，\(h_{T}\)表示最终的输出。好了，有了损失函数，我们就可以对上述的参数进行求导，我们这里以\(U\)为例，根据损失函数，我们得到

\[\frac {\partial L} {\partial U} = \frac {\partial L} {\partial h_{T}} * \frac {\partial h_{T}} {\partial U} \]

我们这里无需关注\(\frac {\partial L} {\partial h_{T}}\),因为这里基本上不影响"梯度爆炸"和"梯度消失"现象的解释。接下来，我们主要对\(\frac {\partial h_{T}} {\partial U}\)进行求导

\[\frac {\partial h_{T}} {\partial U} = \sum\limits_{k=1}^{T} \frac {\partial h_{T}} {\partial z_{k}} * \frac {\partial ^{+} z_{k}} {\partial U} \]

这里\(\frac {\partial ^{+} z_{k}} {\partial U}\)这里表示\(z_{k}\)对\(U\)直接进行求导，即会把这个时刻的\(h_{k-1}\)当成一个常量处理。我们将两个式子分开求导，可以得到

\[\delta_{k} = \frac {\partial h_{T}} {\partial z_{k}} \\ = \frac {\partial h_{T}} {\partial z_{k+1}} * \frac {\partial z_{k+1}} {\partial h_{k}} * \frac {\partial h_{k}} {\partial z_{k}} \\ = \delta_{k + 1} * U * f^{'}(z_{k}) \]

第二个式子,由于这里是直接求导，可以得到

\[\frac {\partial ^{+} z_{k}} {\partial U} = h_{k-1} \]

所以，最终的求导结果为

\[\frac {\partial h_{T}} {\partial U} = \sum\limits_{k=1}^{T} \delta_{k} * h_{k-1} \]

最终\(U\)的优化结果为

\[U^{new} = U^{old} + \alpha * (\frac {\partial L} {\partial h_{T}}) * \sum\limits_{k=1}^{T} \delta_{k} * h_{k-1} \]

那为啥会出现梯度消失和梯度爆炸呢？我们来观察一下这个求导的式子\(\sum\limits_{k=1}^{T} \delta_{k} * h_{k-1}\)。展开之后会发现为

\[\sum\limits_{k=1}^{T} \delta_{k} * h_{k-1} = \delta_{1}h_{0} + \delta_{2}h_{1} + \delta_{3}h_{2} .......\delta_{T}h_{T-1} \\ 更一般地，对于\delta_{k}h_{k-1} = U ^ {T-k} * \prod_{i=k}^{T} f^{'}(z_{i}) * h_{k-1} \]

其中，上式中最小的值为1，也就是会从1一直累乘到T，在RNN中，\(f(z_{k})\)一般用sigmoid，这使得\(f^{'}(z_{i})\)的值基本上在0.25以下，当参数\(U\)初始值较大时，那么\(U^{T}\)是一个非常大的值，在一次更新后，新的\(U\)会变得非常大，会导致梯度爆炸。假如，在初始值\(U\)较小时，经过若干次和sigmoid函数累乘后，数值会变得非常小，那么\(U\)的更新对于最开始的时刻，比如1,2...等时刻变化就非常小，那么开始时刻的信息对梯度的变化贡献就小，而离序列最近的T比如T，T-1.....这些贡献就比较大，这种现象叫做梯度消失。

LSTM

为什么会出现LSTM呢？

由于RNN有"梯度消失"和"梯度爆炸"的现象，那么LSTM就是解决这两个问题才出现的，那么LSTM是如何解决这两个问题的呢？我们接下来进行讨论

LSTM模型结构

LSTM模型的整体逻辑和RNN类似，都会经过一个闭合的隐藏中间单元，不同之处在于RNN只有隐藏权值\(h\)，而LSTM却加入了三个门控单元来解决RNN的"梯度消失"和"梯度爆炸"现象。

• 遗忘门

我们这里先搞一个遗忘门，遗忘门是表示我们希望什么样的信息进行保留，什么样的信息可以通过，所以这里的激活函数是sigmoid。

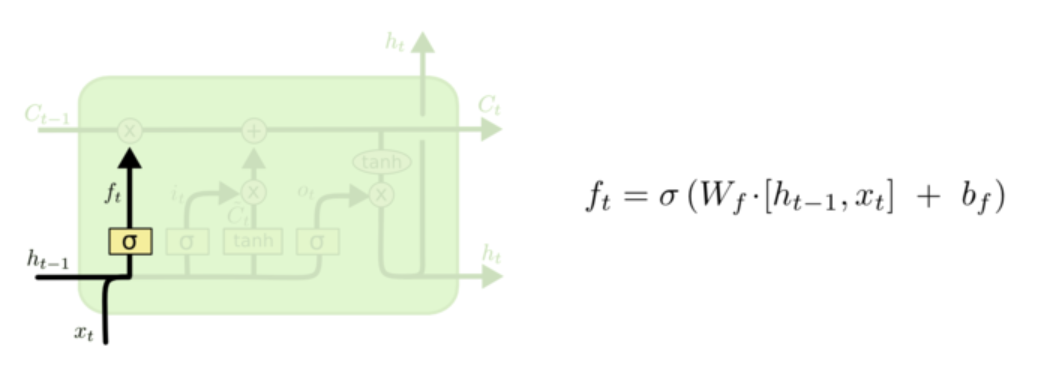
• 输入门

首先，我们用sigmoid建立一个输入门层，决定什么值我们将要更新，接着用tanh建立一个候选值向量，并将其加入到状态中。

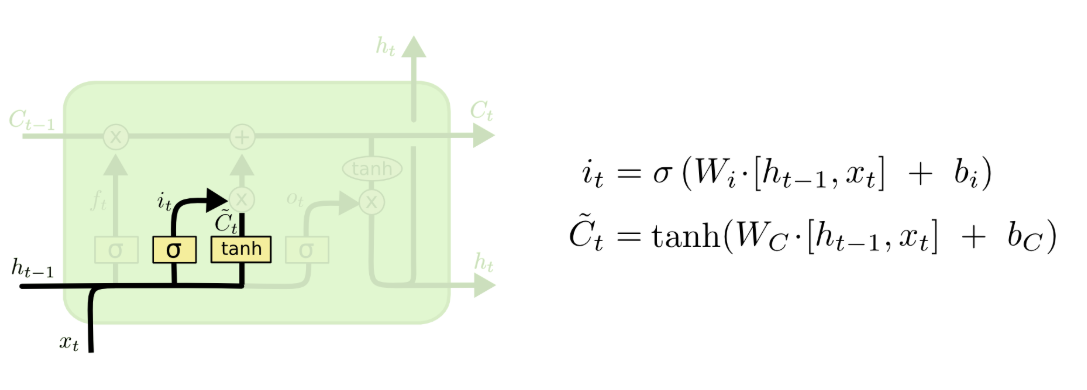
接着，我们就将这些层进行汇总，并更新\(C_{t}\)。如下图所示

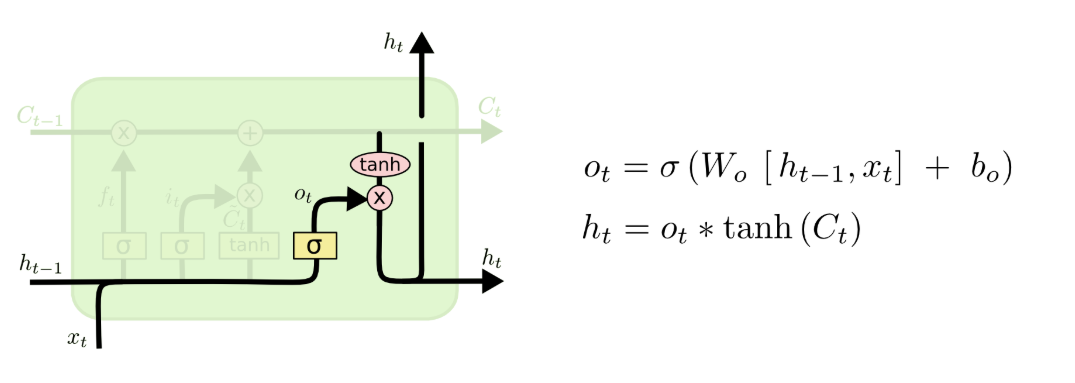
• 输出门

最后我们来到输出门层，更新\(h_{t}\)

2020年6月4日新增理解

这两天看了一些博客和邱锡鹏老师的讲解，对梯度消失和梯度爆炸的理解又更近了一步，接下来说说我对这几个门的理解。梯度消失和梯度爆炸的理解已经加到文章中了。首先，对于梯度消失来说，我们一个直接的想法就是如果有一个记忆单元可以记忆从时刻t=1到t=T的信息就好了，所以就有了\(C(t)\)来保存之前的全部信息，由于乘法操作是控制信息量的流入和流出，而加法操作是将之前的旧信息和当前的新信息进行累加，所以\(C(t)\)的更新的一个想法就是用加法操作，即

\[C_{t} = C_{t-1} + \tilde C_{t} \\ 这里\tilde C_{t}可以表示为当前计算出来需要保留的信息。 \]

但是我们想想，每个时间步的信息我们都需要保留吗？比如当前时刻，我们只需要记住重要的信息就行了，所以就有了输入门即\(i_{t}\)，其控制当前的信息哪些需要流入，哪些流出，就好比人看一句话来说，他只会关注当前句子中重要的字，不重要的不关注。则公式更新为

\[C_{t} = C_{t-1} + i_{t} \otimes \tilde C_{t} \\ 这里\otimes表示说对于信息的控制，因为i_{t}的激活函数是sigmoid函数。后续的遗忘门，输出门也是一样的道理。 \]

但是这里又有一个问题是，\(C_{t}\)会不会由于信息存储的过多，导致信息过多呢？对于人来说，之前的一些记忆我们也会忘记，所以，便有了遗忘门，遗忘门和输入们类似，表示对信息流的控制。

\[C_{t} = f_{t} \otimes C_{t-1} + i_{t} \otimes \tilde C_{t} \]

那最后，我们对记忆单元进行激活，加上一个输出门即可

\[C_{t} = f_{t} \otimes C_{t-1} + i_{t} \otimes \tilde C_{t} \\ h_{t} = o_{t} \otimes tanh(C_{t}) \]

那输入门，遗忘门，输出门以及\(\tilde C_{t}\)的公式为

\[i_{t} = sigmoid(W_{i} * h_{t-1} + V_{i} * x_{t} + b) \\ f_{t} = sigmoid(W_{f} * h_{t-1} + V_{f} * x_{t} + b) \\ o_{t} = sigmoid(W_{o} * h_{t-1} + V_{o} * x_{t} + b) \\ \tilde C_{t} = tanh(W_{c} * h_{t-1} + V_{c} * x_{t} + b) \]

参考文献 [1]如何从RNN起步，一步一步通俗理解LSTM:https://blog.csdn.net/v_july_v/article/details/89894058
[2]RNN 与 LSTM 的原理详解:https://blog.csdn.net/HappyRocking/article/details/83657993