深度学习之文本分类模型-基于RNNs和LSTM系列
1、RNN和LSTM简介
首先我们来简要介绍一下RNN模型和LSTM模型,这样,我们可以很好的理解后面的延伸的模型。可以参考RNN和LSTM模型详解
2、tree-LSTM模型
tree-LSTM是由Kai Sheng Tai[1]等人提出的一种在LSTM基础上改进的一种算法,这是一种基于树的一种算法,论文中提出了两种模型结构,Child-Sum Tree-LSTMs和N-ary Tree-LSTMs。
LSTM是严格按照按照固定的输入序列进行输入,即从头到尾输入单词序列,无法改变顺序。tree-LSTM的思想主要是根据句法分析,语法分析等操作,先构建好一个树,然后根据单词间的相互关系,每个单词分别输入到不同的节点中,通过作者的实验表示,这种方法要比传统的LSTM效果要好。

Child-Sum Tree-LSTMs
根据名字我们可以看出,这是一种将child进行相加的方法。具体操作是什么样的呢?这里假定只考虑一个父节点和其多个子节点的情况,了解了这种情况,对于该父节点的父节点,其实可以依次类推。
给定一个父节点,这个父节点输入的单词序列为\(x_{j}\),子节点的集合为\(C(j)\),注意,这里的\(j\)表示不同的含义,\(x_{j}\)表示的父节点输入的单词vector,第二个\(C(j)\)表示子节点的集合,\(C(1)\)表示第一个孩子。首先,先将子节点的隐藏向量\(h\)进行累加,这也是为啥这个模型叫child-sum的原因了。
接下来,我们计算其他的参数,这里我们要注意一下,\(f_{jk}\)是由每个子节点对应的\(h\)计算而来,而其他的公式则由上个公式\(h_{j}\)计算而来。

最后,更新当前父节点的参数\(c_{j}\)和\(h_{j}\)。
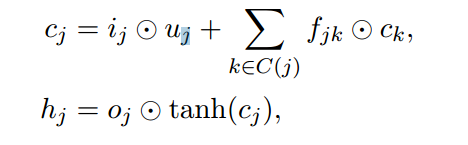
N-ary Tree-LSTMs
这种方法和Child-Sum Tree-LSTMs不同之处在于Child-Sum Tree-LSTMs在计算\(i_{j}\),\(o_{j}\),\(u_{j}\)计算时使用的是每个子节点的隐藏向量加和,而N-ary Tree-LSTMs基本上给这三个输出结果都加上了相应的权值向量\(U\),而不是简单的利用隐藏向量的加和。看下公式

接着得到相应的输出
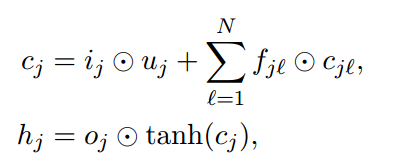
3、MT-LSTM
MT-LSTM(Multi-Timescale Long Short-Term Memory Neural Network)是由复旦大学Pengfei Liu[2]等提出的一种算法,这种方法将LSTM的模型进行了分组,每个组可以选择激活或者不激活,这个由一个函数进行调控,这种方法模拟了人的记忆,激活较多的代表了人的近期记忆,激活少的组代表了人的长久之前的记忆。
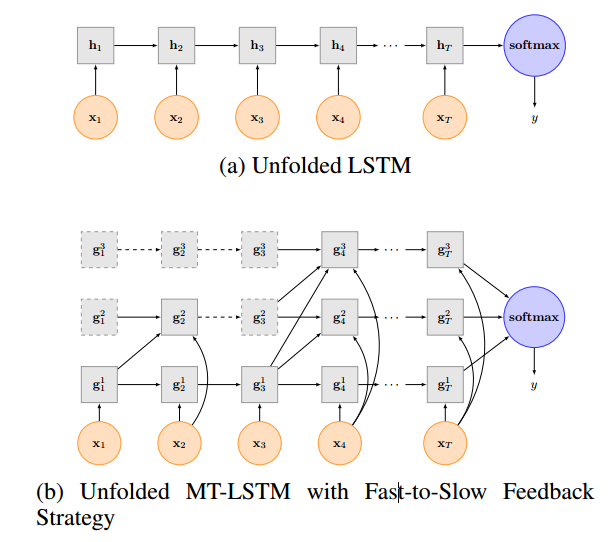
上图中(a)表示的传统的LSTM,(b)表示的MT-LSTM模型,在这个模型中,分了三个组,即\(g^{1},g^{2},g^{3}\),虚线框表示当前时间t该组没有激活,实线框表示该组激活,虚线箭头表示当前节点的权值不进行改变,或者理解为复制上一个节点的权值,实线箭头表示上一个节点参与当前的计算。
- 如何确定某个组在某个时间t是否激活
在论文中,假定了一个公式,即\(t%T_{k} == 0\)则进行激活,这里\(t\)表示时间,也可以理解为单词序列的长度,或者叫句子的长度,\(T_{k} = 2^{k-1}\),上图中的k=1,2,3,则\(T_{1}=1\),\(T_{2}=2\),\(T_{3}=4\)。
在第一个时间步骤,t=1,则第一个组1 % 1 = 0,激活。第二个组1 % 2 = 1,不激活。第三个组1 % 4 = 4,不激活。我们可以看到图中,只有\(g_{1}^{1}\)是实线框,\(g_{1}^{2}\)和\(g_{1}^{3}\)是虚线框。
在第二个时间步,t=2,则第一个组2 % 1 = 0,激活。第二个组2 % 2 = 0,激活。第三个组2 % 4 = 4,不激活。我们可以看到图中,只有\(g_{1}^{1}\)和\(g_{1}^{2}\)是实线框,\(g_{1}^{3}\)是虚线框
依次类推,最终,我们将三个组的结果进行汇总,再接上一个softmax,就可以进行我们后续的操作了。在这一步,我们发现,\(g_{1}^{1}\)无论在哪个时间t,都是激活状态,而越往上的组,激活节点越来越少,所以,最下层的可以理解为人的"短期记忆",即这个组中节点信息保留最多的是最近几个词汇的信息,而最上面一层的节点可以理解为人的"长期记忆"(我们总有一些童年的某件事情使你无法忘怀)。
- 每个节点是如何更新的
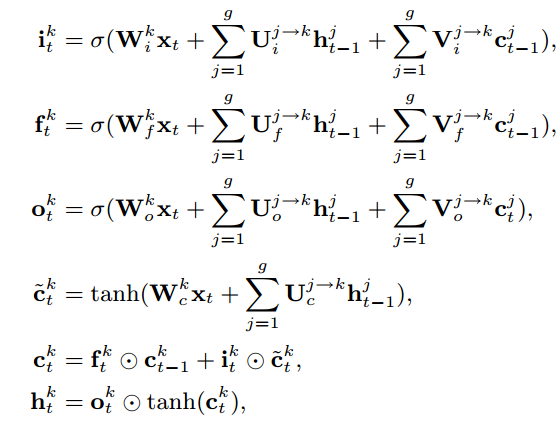
这张图表示的是当前节点若是激活状态下的节点计算方式,其基本计算和传统的LSTM类似,区别在于输入的是上一个时间节点t下的节点状态信息。对于当前节点没有处于激活状态那么怎么办呢?很简单,直接复制呗,如下。
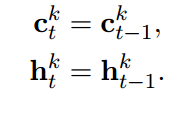
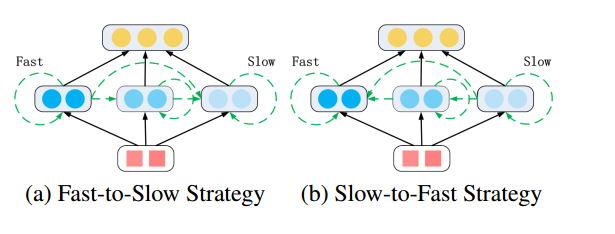
- Fast-to-Slow策略和Slow-to-Fast策略
我们再来观察MT-LSTM的图,从x3到x4的序列上,x4上的所有组都处于激活状态,但是\(g_{4}^{3}\)有分别来自\(g_{3}^{1}\),\(g_{3}^{2}\),\(g_{3}^{3}\)的节点输入,但是\(g_{4}^{1}\)只有来自\(g_{3}^{1}\)的节点输入,这种方式就是Fast-to-Slow策略。这里假定处于底层的组为fast组,上层的组为slow组,fast-to-slow表示上层的组更新,需要上一个时间t的小于它的组级别的输入更新,slow-to-fast则正好相反。我们可以看一下这张图
- 其他
关于论文中作者有一些地方写错了,在此罗列出来,以免后人踩坑。同时也希望我们的研究学者能够对工作更加认真一些。


4、topicRNN
topicRNN是由哥伦比亚大学和微软[3]联合提出的一种算法,将主题模型和RNN进行融合,既融合了主题模型可以获取全局信息的优势,又融合了RNN可以捕获短距离的优势。其基本算法如下所示:
step1:利用高斯分布得到主题向量\(\theta \sim N(0,I)\)
step2:给定一篇文章的单词序列\(y_{1:t-1}\),对于文章中的第t个词
- 根据RNN计算其隐状态,\(h_{t} = f_{W}(x_{t},h_{t-1}), x_{t} \equiv y_{t-1}\)
- 停用词indicator,\(l_{t} \sim Bernoulli(\sigma (\Gamma ^{T} h_{t}))\)
- \(y_{t} \sim p(y_{t} | h_{t}, \theta , l_{t}, B)\) 其中
首先,我们先获得根据高斯分布得到的参数\(\theta\),接下来,我们将单词逐次输入到RNN中,得到每一个隐藏单元\(h_{t}\),当我们得到这些隐藏层单元\(h_{t}\)之后,会通过一个指示器indicator,这个指示器可以看做是一个函数,将\(h_{t}\)进行一个线性变换,再输入到一个sigmoid函数中,我们得到的结果是一个[0,1]之间的数值,这里,用一个伯努利分布,即对于大于0.5的数值输出结果为1,小于0.5的输出结果为0。其中1表示使用停用词,0表示不适用停用词,当指示器为1时,$ b^{T}_{i} \theta$不生效,为0时,不生效。
[2]Pengfei Liu(2015)Multi-Timescale Long Short-Term Memory Neural Network for Modelling Sentences and Documents
[3]Adji B. Dieng(2017)TOPICRNN: A RECURRENT NEURAL NETWORK WITH LONG-RANGE SEMANTIC DEPENDENCY





