AtCoder Beginner Contest 402 ABCDEF 题目解析

A - CBC

题意

给定一个仅由大小写英文字母组成的字符串，请按从前往后的顺序取出所有的大写字母并输出。

思路

模拟即可。输入一个字符串，遍历一遍，遇到大写字母直接输出。

代码

#include<bits/stdc++.h>
using namespace std;

char s[105];

int main()
{
    cin >> s;
    int n = strlen(s);
    for(int i = 0; i < n; i++)
        if(s[i] >= 'A' && s[i] <= 'Z')
            cout << s[i];
    return 0;
}

#include<bits/stdc++.h>
using namespace std;

int main()
{
    string s;
    cin >> s;
    for(char c : s)
        if(c >= 'A' && c <= 'Z')
            cout << c;
    return 0;
}

B - Restaurant Queue

题意

请实现一个队列，完成以下两种操作：

1 X：将数字 \(X\) 加入到队列末尾。
2：输出队首的数字，并让队首出队。

保证每次进行操作 2 时队列均不为空。

思路

队列模板题，直接实现即可。

代码

#include<bits/stdc++.h>
using namespace std;

int q[105];
int f = 1, e = 0; // 队首、队尾

int main()
{
    int n;
    cin >> n;
    while(n--)
    {
        int op;
        cin >> op;
        if(op == 1)
        {
            int x;
            cin >> x;
            q[++e] = x; // 入队
        }
        else
        {
            cout << q[f++] << "\n"; // 队首出队
        }
    }
    
    return 0;
}

#include<bits/stdc++.h>
using namespace std;

int main()
{
    queue<int> q;
    
    int n;
    cin >> n;
    while(n--)
    {
        int op;
        cin >> op;
        if(op == 1)
        {
            int x;
            cin >> x;
            q.push(x);
        }
        else
        {
            cout << q.front() << "\n";
            q.pop();
        }
    }
    
    return 0;
}

C - Dislike Foods

题意

有 \(N\) 种食材，每种食材分别编号为 \(1, 2, \dots, N\)。

餐厅共提供了 \(M\) 个盘子，第 \(i\) 个盘子里的食物由 \(K_i\) 种不同的食材组成，编号分别是 \(A_{i, 1}, A_{i, 2}, \dots, A_{i, K_i}\)。

一开始，Snuke 讨厌所有 \(N\) 种食材。只要某盘食物中存在至少一种他不喜欢的食材，他就不会去吃这一盘食物。

但随着时间一天天过去，他能够慢慢地克服自己不喜欢的食材。在第 \(i\) 天，他不会再不喜欢编号为 \(B_i\) 的食材。

请问，在第 \(i = 1, 2, \dots, N\) 天结束后：

总共有多少盘食物中不包含任何一种 Snuke 不喜欢的食材？（也就是问有多少盘食物他是可以吃的）

思路

（考虑图论），我们可以建立食材 \(\rightarrow\) 盘子这样的关系。

我们可以用一个数组 dislike 统计每个盘子中目前还有多少种食材是他不喜欢的（也就是每个盘子的入度）。

每当有一种食材 \(B_i\) 变得不再不喜欢，我们就可以快速找出所有包含 \(B_i\) 的盘子，然后让每个盘子的 dislike 减一（入度 \(-1\)）。

由于此时只有那些包含食材 \(B_i\) 的盘子的 dislike 才会发生变化，我们可以在减一的同时直接判断是否 dislike 已经变成了 \(0\)。如果是，则说明这个盘子从现在开始就可以吃了，答案加一即可。

代码

#include<bits/stdc++.h>
using namespace std;

int n, m;
vector<int> G[300005];
int dislike[300005];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= m; i++)
    {
        cin >> dislike[i]; // 一开始的食材数量就记作 dislike[i]
        for(int j = 1; j <= dislike[i]; j++)
        {
            int x;
            cin >> x;
            G[x].push_back(i); // 建立食材 x -> 盘子 i 的关系，实现方法有很多
        }
    }
    int ans = 0; // 目前的答案（有多少个盘子已经能吃了）
    for(int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        for(int j : G[x]) // 对于包含食材 x 的每个盘子 j
            if(--dislike[j] == 0) // 如果 -1 后不喜欢的食材数量为 0
                ans++;
        cout << ans << "\n";
    }
    
    return 0;
}

D - Line Crossing

题意

对一个圆进行 \(N\) 等分，并画出每一个 \(N\) 等分点，按顺时针顺序记作 \(1, 2, \dots, N\)。

现在有 \(M\) 条直线，第 \(i\) 条直线会经过 \(A_i\) 和 \(B_i\) 这两个等分点。

问总共有多少对不同的直线存在交点？

思路

我们可以反过来思考，先求出直线的总对数，即 \(\text{C}_{M}^2 = \dfrac{M(M-1)}2\)，然后求有多少对不同的直线不存在交点。

不存在交点即直线平行，那就找平行对的数量即可。

但本题中每条直线经过的两点一定是圆的某两个 \(N\) 等分点，因此可以从这个角度入手思考。

我们可以取每条直线对应的两个等分点 \(A_i, B_i\)，这两个点把整个圆切分成了两半圆弧。并且不难发现，如果两直线平行，那么两段圆弧的中点一定是相同的。如下图所示：

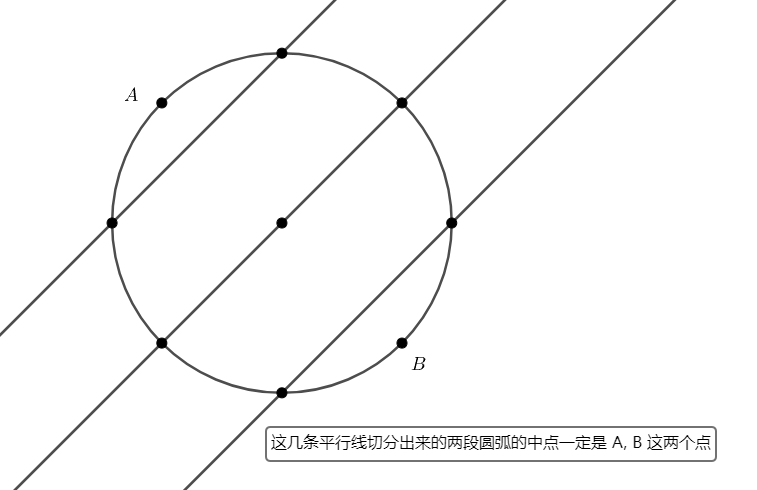
因此我们可以借助中点的编号来确定有多少条直线是平行的。例如，如果以点 \(i\) 作为中点的直线数量共有 \(t_i\) 条，那么平行的直线对数就是 \(\text{C}_{t_i}^2 = \dfrac{t_i(t_{i-1})}2\)，直接从总数中减去即可。

最后，中点的编号正常来说都是采用 \(\dfrac {A_i + B_i} 2\) 来得到的，但有可能计算出上图中两个中点之一。但由于两个中点之间的距离一定是半圆，因此如果编号超过 \(\dfrac N 2\)，我们可以将编号减去 \(\dfrac N 2\) 来统一编号。但，在有些情况下中点可能会出现在两个 \(N\) 等分点之间，因此我们可以去掉除以 \(2\) 这一步骤。去掉后，两个中点的编号距离就变成 \(N\) 了。因此，当计算出来的编号超过 \(N\) 时，直接减去 \(N\) 统一编号即可。

注意数据范围。

代码

#include<bits/stdc++.h>
using namespace std;

int n, m;
int cnt[1000005];
// cnt[i] 统计以 i 作为中点编号的直线数量

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= m; i++)
    {
        int a, b;
        cin >> a >> b;
        int c = a + b; // 求编号
        if(c > n)
            c -= n;
        cnt[c]++; // 以 c 作为中点的直线数量+1
    }
    
    long long ans = 1LL * m * (m - 1) / 2; // 直线对总数
    for(int i = 1; i <= n; i++)
        ans -= 1LL * cnt[i] * (cnt[i] - 1) / 2; // 减去平行直线对数
    cout << ans;
    
    return 0;
}

E - Payment Required

题意

有一场比赛共有 \(N\) 个问题，第 \(i\) 个问题如果解答正确可以获得 \(S_i\) 分，但每解答一次需要花费 \(C_i\) 元钱，并且该题通过的概率是 \(P_i\%\)。

高桥目前共有 \(X\) 元钱，他每次可以任意选择一道还没有通过的题目提交（如果选择已经通过的题目，即使通过了也不会再获得额外的分数）。每次提交的结果都是相互独立的（互不影响）。

每次提交后，高桥可以当场看到提交的结果，然后根据结果来决定要继续提交还是换一道题目提交。

问：当高桥按照某种能够最大化自己的最终得分的策略进行提交，最终他的得分的数学期望值是多少？

思路

在拿到题目后，我们首先可以想到采取期望 dp 的方式解决问题。

定义状态 dp[i][j] 表示考虑到第 \(i\) 道问题为止（第 \(i\) 题可能已经通过也可能未通过，但已考虑过），且此时花费的总金额为 \(j\) 时的最大得分期望值。

对于 dp[i][j]，考虑第 \(i\) 道问题的最后一次提交：

如果此次提交通过，得分就是提交前的期望分值 dp[i - 1][j - c[i]] 加上此题得分 s[i]，概率为 p[i] / 100.0
如果此次提交不通过，由于提交失败是允许反复提交的，因此当前这次提交可能是第一次提交，也可能不是第一次，得分取 max(dp[i - 1][j - c[i]], dp[i][j - c[i]]) 即可，概率为 (100 - p[i]) / 100.0

状态转移方程为：

\[dp[i][j] \xleftarrow{\max} \left \{ \begin{aligned} &dp[i - 1][j] &,\ j \lt C_i \\ &(dp[i - 1][j - C_i] + S_i) \times \frac{P_i}{100} +\max(dp[i - 1][j - C_i], dp[i][j - C_i]) \times \frac{100 - P_i}{100} &,\ j \ge C_i \end{aligned} \right . \]

但在这种转移方式下，我们的答案会受到问题出现顺序的影响。因此我们还需要对于每一种问题的顺序，转移一遍整个方程，最后取 \(dp[n][x]\) 作为当前问题顺序下所得到的得分期望。题目希望最大化自己的得分，因此我们需要在所有可能的答案中再取一个最大值作为最终答案。

动态规划的时间复杂度严格为 \(O(N \cdot X)\)，但枚举 \(N\) 个问题的不同顺序方案数量有 \(N!\) 种，因此最终时间复杂度为 \(O(N! \cdot N \cdot X)\)，会超时。

考虑优化枚举顺序的过程，我们发现可以借助状态压缩的方法来枚举已经考虑过的问题的集合（用二进制 0/1 描述某道题此时是否已经考虑过），这样我们就只需要对于每种集合，去枚举“为了得到当前集合，最后一道需要考虑的题目是哪一道”即可。因此可以再套一层状压 dp。

定义状态 dp[sta][j] 表示当前已经考虑过的所有问题所形成的集合在状态压缩后记作 \(sta\)，且此时花费的总金额为 \(j\) 时的最大得分期望值。

对于 dp[sta][j]，我们可以枚举 \(sta\) 这一集合中所有存在的题目 \(i\)，然后将 \(i\) 从状态 \(sta\) 中去除，得到上一步的状态为 \(pre\)。接下来便可以按照上面讨论过的方法，得出状态转移方程为：

\[dp[sta][j] \xleftarrow{\max} \left \{ \begin{aligned} &dp[sta][j] &,\ j \lt C_i \\ &(dp[pre][j - C_i] + S_i) \times \frac{P_i}{100} +\max(dp[pre][j - C_i], dp[sta][j - C_i]) \times \frac{100 - P_i}{100} &,\ j \ge C_i \end{aligned} \right . \]

集合总数共 \(2^N\) 种，最终时间复杂度为 \(O(2^N \cdot N \cdot X)\)。

代码

#include<bits/stdc++.h>
using namespace std;

int n, x;
int s[10], c[10], p[10];

double dp[256][5005];
// dp[i][j] 表示 考虑到 i 这个集合 且 使用总金额不超过 j 的情况下 的最大期望分值

int main()
{
    cin >> n >> x;
    for(int i = 0; i < n; i++)
        cin >> s[i] >> c[i] >> p[i];
    
    for(int sta = 0; sta < (1 << n); sta++) // 枚举每一种集合
    {
        for(int j = 0; j <= x; j++) // 枚举目前的总金额
        {
            for(int i = 0; i < n; i++) // 枚举每道题
            {
                if(j < c[i]) // 如果当前金额不足以提交当前题目，跳过即可
                    continue;
                if(sta >> i & 1) // 如果 i 题出现在当前集合中
                {
                    int pre = sta ^ (1 << i); // 从当前集合中去掉 i 题，求上一步的状态
                    dp[sta][j] = max(dp[sta][j],
                        (dp[pre][j - c[i]] + s[i]) * p[i] / 100.0
                        + max(dp[sta][j - c[i]], dp[pre][j - c[i]]) * (100 - p[i]) / 100.0
                    );
                }
            }
        }
    }
    
    cout << fixed << setprecision(10) << dp[(1 << n) - 1][x];
    
    return 0;
}

F - Path to Integer

题意

现有一个 \(N \times N\) 的网格，第 \(i\) 行第 \(j\) 列的网格内有一个个位数 \(A_{i, j}\)。

一开始有个人站在左上角 \((1, 1)\) 处，每一步他会向右或向下走一格（如果可以走），直到走完 \(2N-1\) 步后，到达右下角 \((N, N)\)。

然后，他会把过程中遇到的每一个数从前往后串起来，当作一整个数字，然后他的得分就可以记作是这个数字除以 \(M\) 后的余数。

问他的得分最大可以达到多少？

思路

首先，总步数恒定是 \(2N-1\) 步的，并且对于“在网格图上只允许向右或向下走”这个题目模型而言，如果某个格子会被经过，那么“是在第几步经过这个格子”这一问题的答案是确定的。

换言之，每个格子上的个位数对于最终答案的贡献我们可以很方便的预处理出来。

先反向思考，我们直到最后一步是在 \((N, N)\) 上，且最后一步这个格子上的数字在最终的答案中出现在个位，因此最后这个格子的贡献就是 \(A_{N, N} \times 10^0\)。每往回走一步（也就是向左或向上），我们发现所在格子坐标的“行+列”总和总是会 \(-1\)，并且这个格子上的数字在最终的数中所出现的位置会比上一步靠前一位（在十进制下，要乘上的权值便是上一步的 \(10\) 倍）。

那么便可以推导出，对于坐标为 \((i, j)\) 的格子，由于他还需要走 \((N-i) + (N-j)\) 步才能到达右下角，因此这个格子上的数字在最终答案中的贡献权值便是 \(10^{2N-i-j}\)，我们可以直接将贡献记作 \(A_{i, j} \times 10^{2N-i-j}\)。像这样，先把整个 \(A\) 数组处理成最终贡献先。

然后，由于 \(N = 20\)，也就是说如果我们要枚举所有的走法，走法数量可以达到 \(\text{C}_{38}^{19}\)，这是一个非常大的数字，所以我们没法直接去求所有可能的走法。

但因为每一种走法总会经过主对角线（就是整个网格中右上 - 左下的这条线），且到达主对角线时刚好走完总步数的一半，因此我们可以考虑通过折半查找的方法来找出所有的走法，并平衡前后两次查找的时间复杂度。

枚举主对角线上的每个坐标点 \((i, N-i+1)\)，假设该点是主对角线上必须经过的点，于是便可以将走法分为两部分：

从 \((1, 1)\) 走到 \((i, N-i+1)\)
从 \((i, N-i+1)\) 走到 \((N, N)\)

对于第一部分，直接暴力搜索，找出所有可能的走法，并求出每一种走法所经过的格子的贡献总和（除以 \(M\) 取余数），用 set 等容器先记录下来。

然后再对于第二部分，也是暴力搜索找所有可能的走法，但在求出每种走法的贡献总和后，由于最终的答案是通过当前第二部分这种走法的贡献加上第一部分的某一种走法的贡献得来的，为了让答案能够取到最大，我们可以借助贪心策略在刚才的容器当中找出一个数字，并且让两部分贡献相加最大。这里我们记当前第二部分搜索出来的贡献为 sum（已除以 \(M\) 取余数），分类讨论如下：

如果第一部分的贡献加上 sum 不会超过 \(M\)（也就是不用取余），那么为了让最终答案最大，我们需要在第一部分的所有贡献当中找出 \(\lt M - sum\) 的最大贡献。可以借助二分来完成查找。
如果第一部分的贡献加上 sum 可能会超过 \(M\)，由于两个 \(M\) 以内的数相加不会达到 \(2M\) 的大小，我们就直接取第一部分的所有贡献当中最大的那种贡献加上即可。对于 set 容器可以直接取尾指针的前一个位置作为答案。

两种情况都考虑一遍，取最大答案即可。

最后分析时间复杂度。这种折半查找的方法只需要考虑两次从边角走到主对角线的方案数。我们以从 \((1, 1)\) 往右下走为例，由于在主对角线之前，每一步向右或向下都可以走，不会碰到不能走的情况，因此这 \(N-1\) 步内的每一步都有两种方案，总方案数便是 \(2^{N-1}\)。后半部分的方案数也是 \(2^{N-1}\)，这里的时间复杂度便可以记作 \(O(2^N)\)。然后在搜索完第一部分之后，对于第二部分搜出来的每一种贡献，都需要借助二分去尝试找最优解，因此这一步的时间复杂度可以简单记作 \(O(\log 2^N)\)。

最终的时间复杂度为 \(O(2^N \log 2^N)\)。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int n;
ll mod;
ll a[25][25];
ll n10[45];

ll ans = 0; // 答案

set<ll> st; // 存第一部分搜到的所有走法贡献

// 折半查找 往左上角走（倒着走）
void dfs1(int x, int y, ll sum)
{
    if(x == 1 && y == 1) // 到达 (1, 1)，记录这种方案的贡献
    {
        st.insert(sum);
        return;
    }
    if(x > 1) // 往上走
        dfs1(x - 1, y, (sum + a[x - 1][y]) % mod);
    if(y > 1) // 往左走
        dfs1(x, y - 1, (sum + a[x][y - 1]) % mod);
}

// 折半查找 往右下角走
void dfs2(int x, int y, ll sum)
{
    if(x == n && y == n) // 到达 (n, n)，分类讨论求最大答案 
    {
        auto it = st.lower_bound(mod - sum); // 第一种情况，先二分找 >= mod-sum 的最小值
        if(it != st.begin())
        {
            it--; // 想要的数字是 <mod-sum 的最大值，所以要获得前一个位置，指针左移
            ans = max(ans, sum + (*it));
        }
        it = --st.end(); // 第二种情况，取 set 内的最大值，直接取 set 的尾指针前一个位置
        ans = max(ans, (sum + (*it)) % mod);
        return;
    }
    if(x < n) // 往下走
        dfs2(x + 1, y, (sum + a[x + 1][y]) % mod);
    if(y < n) // 往右走
        dfs2(x, y + 1, (sum + a[x][y + 1]) % mod);
}

int main()
{
    cin >> n >> mod;
    
    n10[0] = 1;
    for(int i = 1; i <= 2 * n; i++)
        n10[i] = n10[i - 1] * 10 % mod; // n10[i] 存 10^i % mod 的结果
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
        {
            cin >> a[i][j];
            int pw = 2 * n - (i + j); // 走到右下角还有多少步
            a[i][j] = a[i][j] * n10[pw] % mod; // a[i][j] 改为该位置对答案的贡献
        }
    
    for(int i = 1; i <= n; i++)
    {
        // 枚举主对角线上的每一个位置 (i, n-i+1)
        // 假设当前方案一定会经过这个格子
        int j = n - i + 1;
        st.clear(); // 清空集合
        dfs1(i, j, a[i][j]); // 第一部分，搜索左上角到该位置的所有方案，a[i][j] 放任意一边均可
        dfs2(i, j, 0); // 第二部分，搜索该位置到右下角的所有方案
    }
    
    cout << ans;
    
    return 0;
}

posted @ 2025-04-19 23:06 StelaYuri 阅读(234) 评论(2) 收藏举报

刷新页面返回顶部

StelaYuri