2022年蓝桥杯软件类省赛 C/C++ B组 解析

前两年题解都是学长写的，今年到我了QAQ

今年题目相比于去年的大致上变简单了，但该坑的地方还是坑

题目和赛时代码都没存，提早溜了，所以本文内代码可能大概或许似乎应该不一定完全和早上敲的一样

我们学校是线下借机房进行比赛的，出来后网上冲浪划水才知道原来今年甚至有线上的（？）

写这篇题解的过程中我逐渐想不起赛时到底在想些什么又写了些什么现在很慌感觉好多东西现在能理清楚但忘了早上有没有想清楚了呜呜呜

最后再提醒一句，数据量大的题目用 $cin/cout$ 记得关同步流，下面的代码为了简洁就省略掉了

$UPD$： $H$ 题代码更改。
$UPD\ 2$： 加入了题面。
$UPD\ 3$： $E$ 题补充了对于负数的讨论，但结论不变。
$UPD\ 4$ - 2022/12/17： $E$ 题代码错误变更（官网数据太弱了吧），$J$ 题代码更改+坑点解释。

A - 九进制转十进制

$(2022)_9 = 2*9^3+0*9^2+2*9^1+2*9^0 = 1478$

签到成功！

B - 顺子日期

这比赛每年都会有那么一两道啥b题，习惯了，自以为提出了一个妙妙的东西，然后题目里甚至一点都不进行解释，出题的就搁这摆

兹认为，这题是全场最啥b题

“顺子指的就是连续的三个数字”：连续递增？连续递减？

“例如 $20220123$ 就是一个顺子日期，因为它出现了一个顺子：$123$”：出现了一个顺子 $123$，难道表示 $012$ 不是顺子？

所以这题就纯纯的在猜谜语

至于答案呢，如果 $012$ 不算，就只有可能是 $123$，用手指掰一掰都能枚举出来就 $0123,1123,1230,1231$ 这四种月日组合情况，答案 $4$

如果 $012$ 算，上面四种加上 $012x$ 和 $1012$，答案 $14$

这题大家应该要么 $4$ 要么 $14$ 吧，反正我写的 $14$，最后高低还得骂两句

C - 刷题统计

原题？这种题目 CF 上感觉都做过好多次，C 语言入门题

以一周为单位，一周做 $5a+2b$ 道题，故天数至少 $\lfloor\frac n {5a+2b}\rfloor \times 7$

然后让 $n$ 对 $5a+2b$ 取模，最后一周暴力跑跑就行

void solve()
{
    ll a,b,n;
    cin>>a>>b>>n;
    
    ll d=5*a+2*b;
    ll ans=n/d*7;
    n%=d;
    
    for(int i=1;i<=5;i++)
        if(n>0)
        {
            n-=a;
            ans++;
        }
    for(int i=1;i<=2;i++)
        if(n>0)
        {
            n-=b;
            ans++;
        }
    cout<<ans<<'\n';
}

D - 修建灌木

明显对于第 $i$ 个位置的灌木，要么是爱丽丝修剪完它后向左走再走回来剪，要么就是剪完向右再回来

要求最高的高度，那就向左向右取个最大距离乘上 $2$ 就是答案了

假设剪完 $i$ 后向左，下一次再剪 $i$ 就是 $(i-1)\times 2$ 天后；

假设剪完 $i$ 后向右，下一次再剪 $i$ 就是 $(n-i)\times 2$ 天后。

void solve()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cout<<max(i-1,n-i)*2<<'\n';
}

E - X 进制减法

证明：

因为两个数使用同一进制规则，假设第 $i$ 位为 $a_i$ 进制 （从低往高，假设 $i=0$ 为最低位）

再定义 $b_i = \prod_{j=0}^{i-1} a_j$

明显，对于该规则下的进制数 $A$，其十进制值就是 $A_0b_0+A_1b_1+\cdots+A_nb_n$

同样的，$B$ 的十进制值就是 $B_0b_0+B_1b_1+\cdots+B_mb_m$

（这里注意，题目里保证了 $A\gt B$，且使用同一进制规则，因此 $n\ge m$ 恒满足）

现在我们要让 $A-B$ 的结果尽可能小

两式子相减，得到 $(A_0-B_0)b_0+(A_1-B_1)b_1+\cdots+(A_m-B_m)b_m+A_{m+1}b_{m+1}+\cdots+A_nb_n$

已知 $(A_0-B_0),\ (A_1-B_1)$ 这些值是定值，如果是正数，那我们只能是让 $b_i$ 取得尽可能小，也就是让上面假设的 $a_i$ 尽可能小

但如果对于某个位置 $(A_i-B_i)$ 是负数呢？负数的话我们就应该让 $b_i$ 尽可能大啊？

其实根据题目 $A\ge B$ 的限制可知，一定会有更高位 $j\gt i$ 使得 $(A_j-B_j)$ 是正数

又因为 $b_i$ 是由 $a_0$ 连乘到 $a_{i-1}$ 的，所以较低位 $b_i$ 如果取得越大，那么 $b_{i+1},b_{i+2}$ 等更高位也是会跟着变大的，且变大的级数较低位而言更大

明显这样子两数相减的结果会因为高位变大而变大，所以不论 $(A_i-B_i)$ 正负如何，进制都应当尽可能小

综上，让每个位置的进制等于 $A,B$ 两个数该位置的较大值 $+1$ 就是答案

贪心：

第 $i$ 位置的进制 $a_i = \max(A_i,B_i) + 1$，注意最低进制为 $2$，再与 $2$ 取个 $\max$

然后在取模意义下单独把 $A,B$ 两个数的值求出来，$(A-B+mod)\% mod$ 就是答案

给定数据的第一个数 $n$ 只是提了一下最大进制，但实际上没用

还有就是坑点在长度不相同的时候，多造些例子测测，我忘了当时怎么写的了现在很慌，但跟下面这份代码应该不一样

// 忘了数据范围多大了，数组随便开开
const ll mod=1e9+7;

int x,n,m;
int A[100050],B[100050];
int C[100050];

void solve()
{
    cin>>x;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>A[i];
    cin>>m;
    for(int i=1;i<=m;i++)
        cin>>B[i];
    
    int len=max(n,m);
    for(int i=len;i>=1;i--)
    {
        C[i]=2;
        if(n-(len-i)>0)
            C[i]=max(C[i],A[n-(len-i)]+1);
        if(m-(len-i)>0)
            C[i]=max(C[i],B[m-(len-i)]+1);
    }
    
    ll AA=0,BB=0;
    for(int i=1;i<=len;i++)
    {
        if(n-(len-i)>0)
            AA=(AA*C[i]+A[n-(len-i)])%mod;
        if(m-(len-i)>0)
            BB=(BB*C[i]+B[m-(len-i)])%mod;
    }
    
    cout<<(AA-BB+mod)%mod<<'\n';
}

F - 统计子矩阵

又是一道既视感极强的题目呢

由于题目数据保证每个位置的值为非负数，不需要考虑那么多

二维前缀和预处理一下，然后 $O(n^2)$ 枚举子矩阵左上角 $(x,y)$

如果考虑暴力，再 $O(n^2)$ 枚举右下角，对于 $n=500$ 的数据明显不大行

假设子矩阵当前只有一行，且满足条件的子矩阵右端点能到达坐标 $(x,r)$ 处

那么这一行满足条件的子矩阵数量就是 $r-y+1$

考虑往下扩一行，明显 $(x,y)$ 到 $(x+1,r)$ 的和变大了，因此通过前缀和来维护右边界 $r$，尝试左移到第一个位置满足 $(x,y)\sim(x+1,r)$ 的和满足条件位置，答案还是 $r-y+1$

可以发现右边界 $r$ 随着下边界的下移是单调递减的

继续这样做下去，直到枚举到第 $n$ 行，或者 $r\lt y$ 为止

这种做法的时间复杂度为 $O(n)$

总时间复杂度为 $O(n^3)$ ，勉强可以过，注意写法即可

int a[505][505];
ll s[505][505];

void solve()
{
    int n,m,k;
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>a[i][j];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
    ll ans=0;
    for(int i=1;i<=n;i++) // 上
        for(int j=1;j<=m;j++) // 左
        {
            int r=m; // 右
            for(int u=i;u<=n;u++) // 下
            {
                while(s[u][r]-s[i-1][r]-s[u][j-1]+s[i-1][j-1]>k)
                    r--;
                if(r<j)
                    break;
                ans+=r-j+1;
            }
        }
    cout<<ans<<'\n';
}

G - 积木画

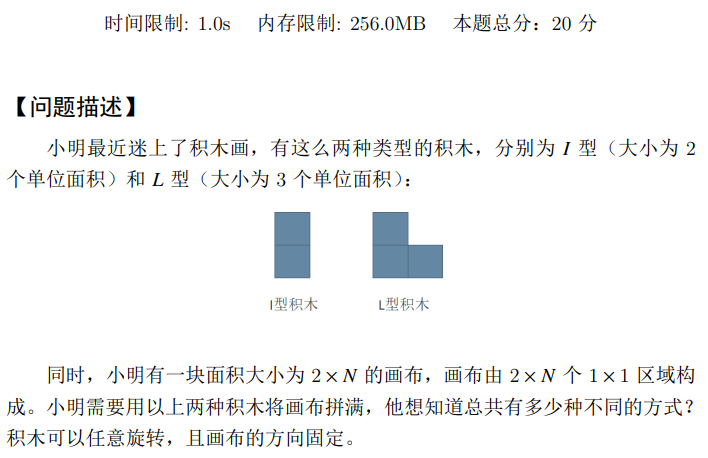
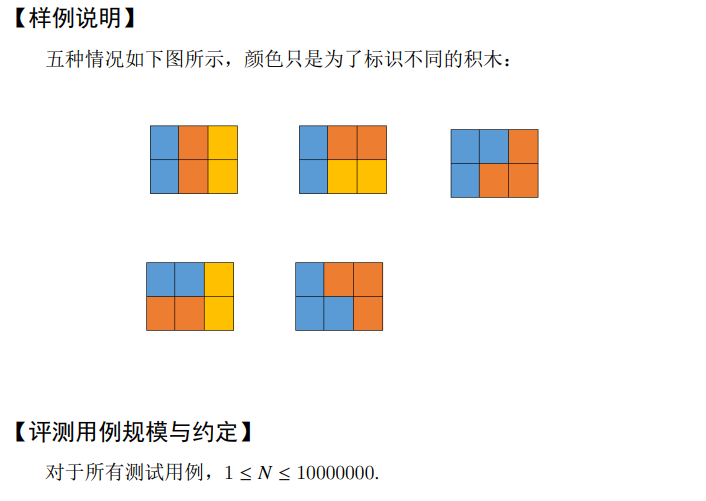
考虑 DP

定义 $dp[i=1\sim n][j=0\sim 2]$ 表示往前 $2\times i$ 的画布中填充积木的方案数

其中 $j=0$ 时表示第 $i$ 列上下两个格子都被填充了，且 $i-1$ 列之前的所有格子都全部已填充

$j=1$ 表示第 $i$ 列上边的格子没有被填充，且 $i-1$ 列之前的所有格子都全部已填充

$j=2$ 表示第 $i$ 列下边的格子没有被填充，且 $i-1$ 列之前的所有格子都全部已填充

考虑初始状态：

$dp[1][0]=1$

$dp[2][0]=2,\ dp[2][1]=dp[2][2]=1$

考虑状态转移：

• $dp[i][0]$ 可以由下图中四种状态转移而来

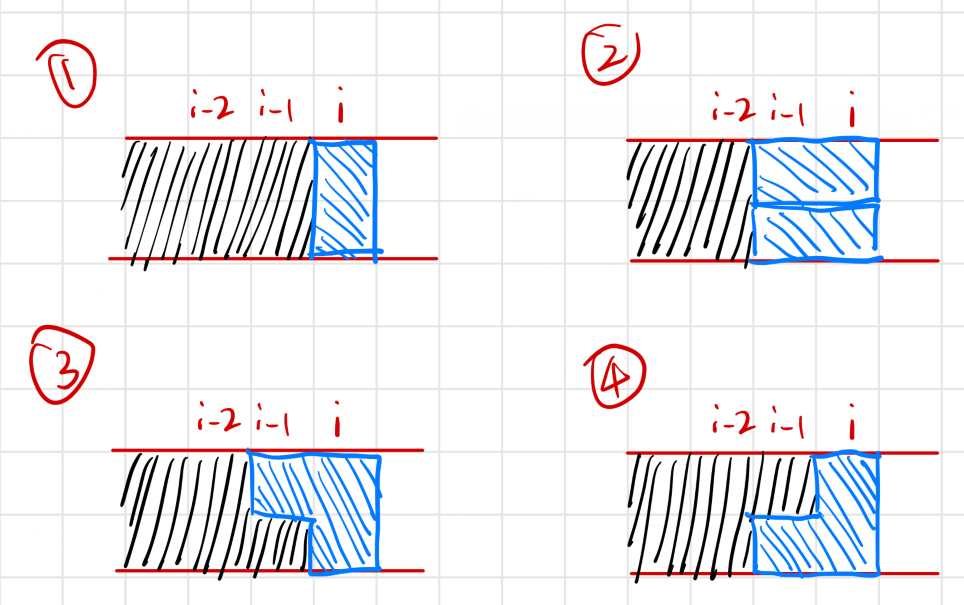
第一种的前置情况等同于 $dp[i-1][0]$

第二种的前置情况等同于 $dp[i-2][0]$

第三种的前置情况等同于 $dp[i-1][1]$

第四种的前置情况等同于 $dp[i-1][2]$

• $dp[i][1]$ 可以由下图中两种状态转移而来

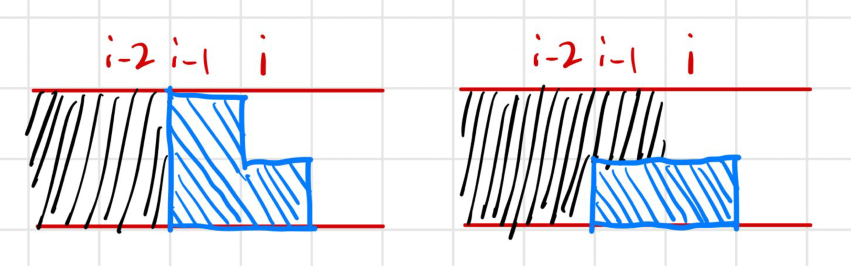
左边的前置情况等同于 $dp[i-2][0]$

右边的前置情况等同于 $dp[i-1][2]$

• $dp[i][2]$ 与上图类似，上下翻转一下

两种情况分别是 $dp[i-2][0]$ 与 $dp[i-1][1]$

然后就可以直接敲代码了

const ll mod=1e9+7;

ll dp[10000050][3];

void solve()
{
    int n;
    cin>>n;
    dp[1][0]=1;
    dp[2][0]=2;
    dp[2][1]=dp[2][2]=1;
    for(int i=3;i<=n;i++)
    {
        dp[i][0]=dp[i-1][0]+dp[i-2][0]+dp[i-1][1]+dp[i-1][2];
        dp[i][1]=dp[i-2][0]+dp[i-1][2];
        dp[i][2]=dp[i-2][0]+dp[i-1][1];
        dp[i][0]%=mod;
        dp[i][1]%=mod;
        dp[i][2]%=mod;
    }
    cout<<dp[n][0]<<'\n';
}

悄咪咪地考虑一下小优化

打个小表：$1,2,5,11,24,53,117,258,569,1255$

猜想一下，这个数列应该满足 $a_i=2a_{i-1}+x$ 这个样子的

然后再手算一下，发现式子就出来了

$a_i=2a_{i-1}+a_{i-3}$

于是常数就变小了~

const ll mod=1e9+7;

ll a[10000050];

void solve()
{
    int n;
    cin>>n;
    a[1]=1;
    a[2]=2;
    a[3]=5;
    for(int i=4;i<=n;i++)
        a[i]=((a[i-1]<<1)+a[i-3])%mod;
    cout<<a[n]<<'\n';
}

H - 扫雷

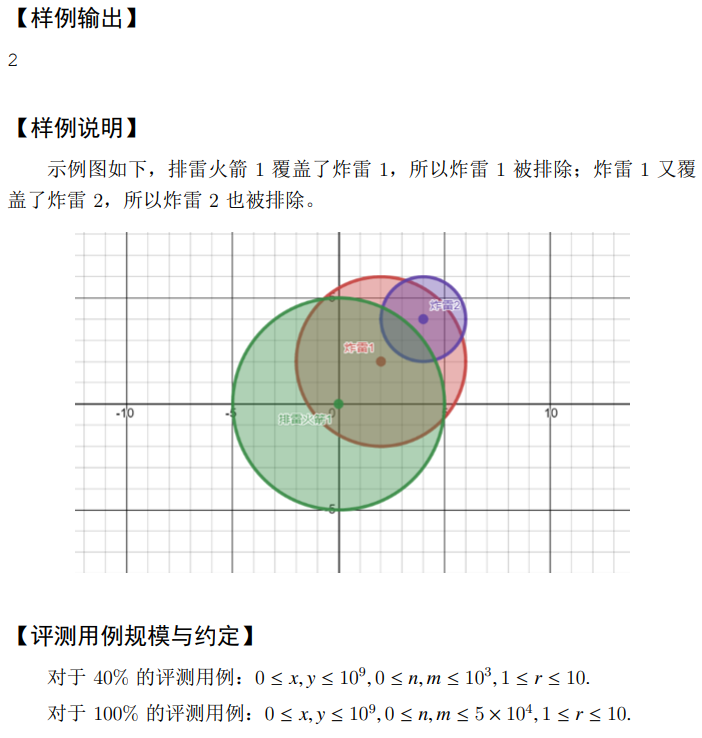
首先，数量的数据范围比较大，不能像传统方式那样 $O(n^2)$ 来求某个圆覆盖哪些点

但是发现 $r$ 很小，于是考虑暴力求 $(x\pm r,y\pm r)$ 这一范围内有哪些点就行啦

然后题目又说同一点上可能存在多个点

于是使用 map<Point,Rmax> 存储圆心位于点上时的最大半径，另一个 map 存有多少个圆圆心位于该点

遍历每个炸弹可能炸到的点，如果该点存在地雷，则从该点继续 dfs 搜索即可

typedef pair<int,int> P;

map<P,int> mpr,mpcnt;
int ans=0;

inline bool isPointOnCircle(int xx,int yy,int x,int y,int r)
{ // 尽可能不要用浮点数计算
    return (xx-x)*(xx-x)+(yy-y)*(yy-y)<=r*r;
}

void dfs(int x,int y,int r)
{
    int xmn=x-r,xmx=x+r;
    int ymn=y-r,ymx=y+r;
    for(int xx=xmn;xx<=xmx;xx++)
        for(int yy=ymn;yy<=ymx;yy++) // 枚举2r*2r大小的矩阵内所有点
        {
            if(!isPointOnCircle(xx,yy,x,y,r))
                continue;
            P point=P(xx,yy);
            if(mpr.count(point)) // 如果该点地雷未被访问过
            {
                ans+=mpcnt[point];
                int rr=mpr[point];
                mpr.erase(point); // 删掉这个键值，表示访问过了
                dfs(xx,yy,rr);
            }
        }
}

void solve()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        int x,y,r;
        cin>>x>>y>>r;
        mpr[P(x,y)]=max(mpr[P(x,y)],r);
        mpcnt[P(x,y)]++;
    }
    for(int i=1;i<=m;i++)
    {
        int x,y,r;
        cin>>x>>y>>r;
        dfs(x,y,r);
    }
    cout<<ans<<'\n';
}

I - 李白打酒加强版

标准滚动数组 DP（也可以不滚动直接DP），或者直接记搜也可以

定义数组 $dp[s][t][a][b]$ 表示前 $s$ 次事件中，遇到了 $a$ 次店、$b$ 次花，酒还剩 $t$ 斗的方案数

初始状态 $dp[0][2][0][0]=1$

事件最多 $n+m=200$ 次，酒的次数应当不超过还剩余的遇见花的次数，最大为 $100$

但这样数组大小就是 $(n+m)\times n\times m^2$，空间太大了

发现对于合法的 $dp[s][t][a][b]$，$s=a+b$ 是恒成立的，且每次状态转移都是 $s+1$，然后 $a$ 或者 $b$ 加上 $1$

因此可以让 $s$ 进行滚动，且后面的状态不会引用两步及之前的状态，转移前也不需要清空滚动数组

转移的话就很简单了，考虑转移到 $dp[s][t][a][b]$ 的前置状态：

• $dp[s-1][\frac t 2][a-1][b]$ 可以成为前置状态，条件是 $t$ 为偶数且 $a\gt 0$
• $dp[s-1][t+1][a][b-1]$ 可以成为前置状态，条件是 $b\gt 0$

最后，注意一下题目里提及最后一次遇见的是花，因此答案应该是 $dp[n+m-1][1][n][m-1]$ 而不是 $dp[n+m][0][n][m]$（当时我还以为自己敲错了）

UPD: s,a,b 三维直接去掉一维也可以QAQ，那就不用滚动了

const int mod=1e9+7;

int dp[2][101][101][101];

void solve()
{
    int n,m;
    cin>>n>>m;
    dp[0][2][0][0]=1;
    for(int s=1;s<n+m;s++)
        for(int t=0;t<=min(m,n+m-s);t++) // 酒的斗数不能超过接下来的步数，下面还能再缩小范围
        {
            int cur=s&1,pre=cur^1;
            for(int a=0;a<=n;a++)
            {
                int b=s-a;
                if(b>m||b<0||t>m-b) // 如果b不合法或者剩余的酒太多了
                    continue;
                if(!(t&1)&&a>0)
                    dp[cur][t][a][b]+=dp[pre][t/2][a-1][b];
                if(b>0)
                    dp[cur][t][a][b]+=dp[pre][t+1][a][b-1];
                dp[cur][t][a][b]%=mod;
            }
        }
    cout<<dp[(n+m-1)&1][1][n][m-1]<<'\n';
}

J - 砍竹子

最后一题了，本来还以为只能整个区间 DP 啥的骗骗分呢，结果怎么也想不出来怎么 DP

然后换了一种思路想了一遍，发现直接把相邻的尝试合并就可以了（

合并的意思是这样子的，比如对于两个相邻位置，一个值是 $6$ ，另一个值是 $7$

根据题意，$6$ 单独进行操作，过程是 $6\rightarrow 2\rightarrow 1$

$7$ 单独进行操作，过程是 $7\rightarrow 2\rightarrow 1$

这两个数字在操作过程中均出现了 $2$，也就说明我们可以将这两个不同的数先单独操作，使其都变成 $2$，然后两个就可以合并起来看一起操作了

因此可以直接从左往右看相邻的数，如果左边的数在操作过程中出现的数字与右边的数操作过程中出现的数存在相同，那么就可以先单独进行操作，再一起进行操作

就比如样例，先单独将过程画出来，如下图左，然后在处理数字 $6$ 时，发现其处理过程存在 $2$，与其左侧的数有重叠部分，那么我们就只把 $6\rightarrow 2$ 这一过程中使用的次数加入答案即可；数字 $7$ 同理，因此下图中被圈起来的箭头就是计入答案的数量

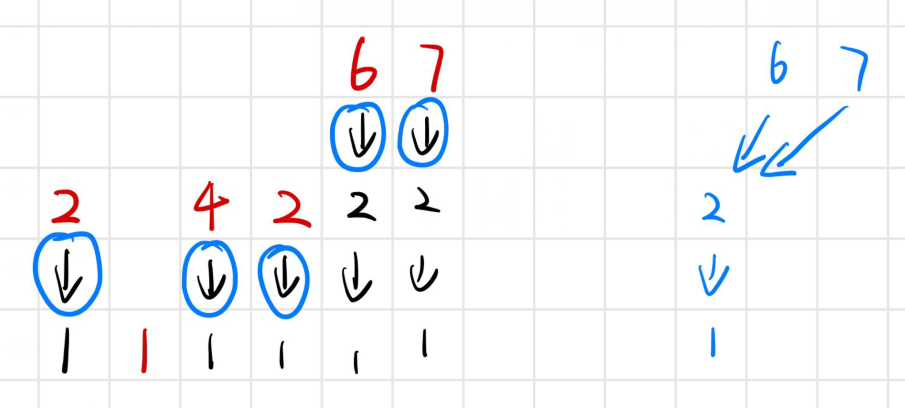
最后，题目给定的式子操作次数是不超过 $\log$ 级别的，暴力跑一下 $10^{18}$ 可以发现只需要执行 $6$ 次，所以查找重叠数字的这一步就直接 map/set 暴力整即可

总体复杂度 $O(n\times 6\log 6)$

UPD：注意，有大部分测试点卡了 sqrt 函数，所以这部分需要手写一个整数二分。

typedef long long ll;

ll a[200050];
map<ll,int> mp;

int SQRT(ll d)
{
    int l=0,r=1e9;
    while(l<=r)
    {
        int m=(l+r)/2;
        if(1LL*m*m<=d)
            l=m+1;
        else
            r=m-1;
    }
    return r;
}

int trans(ll d)
{
    return SQRT(d/2+1);
}

int sol(ll d) // 查询需要多进行的操作数
{
    int r=0;
    while(d>1)
    {
        if(mp.count(d))
            return r;
        d=trans(d);
        r++;
    }
    return r;
}

void ins(ll d) // 将map改为d的变化过程
{
    mp.clear();
    while(d>1)
    {
        mp[d]=1;
        d=trans(d);
    }
}

void solve()
{
    int n,ans=0;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=1;i<=n;i++)
    {
        ans+=sol(a[i]);
        ins(a[i]);
    }
    cout<<ans<<'\n';
}

就无了，祝好运，哭哭