Codeforces 1477C/1478F - Nezzar and Nice Beatmap （几何/暴力）

Codeforces Round #698 (Div.1) - C

Codeforces Round #698 (Div.2) - F

题意

给定\(n\)个点，要求构造一个点的排列，连成一条路线后使得每个\(\ang ABC\lt 90°\)（每个拐角需要拐\(\gt 90°\)）

如下图左为可行路线，右为不可行路线

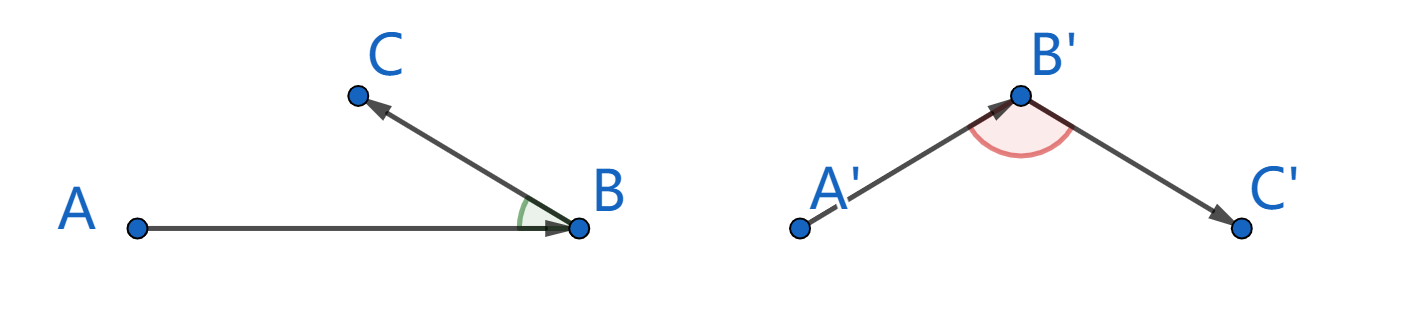
保证不存在重合的点，不存在方案输出\(-1\)

限制

\(3\le n\le 5000\)

思路

假设我们现在找到了一段合法路线，其中\(A,B\)为目前这条合法路线的最后两点

结论：

我们只需要找出还不存在于路线中的点\(C\)，使得\(|BC|\)最大，这样点\(C\)就能成为下一个点

接下来就继续找点\(D\)满足\(|CD|\)最大即可

最后输出点序即可，所以不存在\(-1\)的情况

至于第一个点，实际上取任意一点均可（保险起见我取的是排序后第一个点）

时间复杂度\(O(n^2)\)

证明：

如果我们接下来找的点\(C\)能够满足\(|BC|\)最大（或并列大）

以\(B\)为圆心，\(|BC|\)为半径作一个圆，剩下的所有点肯定都落在这个圆内（或圆上）

由于不存在重合的点，明显对于任意剩下的点\(D\)，\(\ang BCD\lt 90°\)恒成立

那么对于\(\ang ABC\)，假设\(\ang ABC\ge 90°\)，明显可以发现\(|AC|\gt|AB|\)成立，那么\(A\)的下一个点必不可能是\(B\)，与我们的假设“其中\(A,B\)为目前这条合法路线的最后两点”不符，所以可得\(\ang ABC\lt 90°\)成立

程序

(140ms/2000ms)

// StelaYuri
//#include<ext/pb_ds/assoc_container.hpp>
//#include<ext/pb_ds/hash_policy.hpp>
#include<bits/stdc++.h>
#define closeSync ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define multiCase int T;cin>>T;for(int t=1;t<=T;t++)
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i<(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define perr(i,a,b) for(int i=(a);i>(b);i--)
#define pb push_back
#define eb emplace_back
#define mst(a,b) memset(a,b,sizeof(a))
using namespace std;
//using namespace __gnu_pbds;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const double eps=1e-12;
const double PI=acos(-1.0);
const double angcst=PI/180.0;
const ll mod=998244353;
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
ll qmul(ll a,ll b){ll r=0;while(b){if(b&1)r=(r+a)%mod;b>>=1;a=(a+a)%mod;}return r;}
ll qpow(ll a,ll n){ll r=1;while(n){if(n&1)r=(r*a)%mod;n>>=1;a=(a*a)%mod;}return r;}
ll qpow(ll a,ll n,ll p){ll r=1;while(n){if(n&1)r=(r*a)%p;n>>=1;a=(a*a)%p;}return r;}

struct point
{
    ll x,y;
    int id;
    bool vis;
    bool operator <(const point& a) const
    {
        if(x^a.x)
            return x<a.x;
        return y<a.y;
    }
}ar[5050];

ll distance(int a,int b)
{
    return (ar[a].x-ar[b].x)*(ar[a].x-ar[b].x)+(ar[a].y-ar[b].y)*(ar[a].y-ar[b].y);
}

void solve()
{
    int n;
    cin>>n;
    rep(i,1,n)
        cin>>ar[i].x>>ar[i].y,ar[i].id=i,ar[i].vis=false;
    sort(ar+1,ar+1+n);
    
    ar[1].vis=true;
    cout<<ar[1].id;
    int p=1;
    
    rep(i,2,n)
    {
        ll d=0;
        int nxt=0;
        
        rep(j,1,n)
            if(!ar[j].vis) //没用过的点
            {
                if(!nxt)
                {
                    nxt=j;
                    d=distance(p,j);
                }
                else
                {
                    ll dd=distance(p,j);
                    if(dd>d) //取距离最大的点
                    {
                        nxt=j;
                        d=dd;
                    }
                }
            }
        
        ar[nxt].vis=true;
        p=nxt;
        cout<<' '<<ar[nxt].id;
    }
}
int main()
{
    closeSync;
    //multiCase
    {
        solve();
    }
    return 0;
}