AtCoder "Regular Contest 102" D - All Your Paths are Different Lengths （构造）

Regular Contest 102 - D - All Your Paths are Different Lengths

题意

给定一个\(L\)，要求构造出一个点数\(n\)不超过\(20\)，边数\(m\)不超过\(60\)的有向图（允许存在重边）

保证该图从点\(1\)到点\(n\)存在恰好\(L\)种不同的路径，每条路径权值和互异，且在\([0,L-1]\)之间

限制

\(2\leq L\leq 10^6\)

思路

第一部分

考虑\([0,L-1]\)内数字的二进制表示法

由于每个数字都能表示成多个\(2\)的次方幂之和，换句话说，为了表示出某个数字，对于每个\(2\)的次方幂可以决定是选还是不选（二进制上\(1\)表示选择，\(0\)表示不选）

以有向图进行表示，则可以按顺序连接两条\(i\)到\(i+1\)的边，一条权值为\(2^{i-1}\)表示选择，一条权值为\(0\)表示不选择

得到的有向图如下图所示：

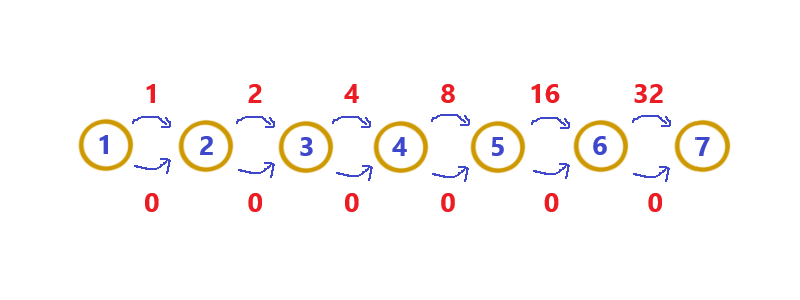
上图从第\(1\)个点走到第\(7\)个点，所能表示的数值范围为\([0,111111B=63]\)

第二部分

但发现题目限制\(n\leq 20\)，因此最多只能够表示到\(2^{18}=262144\)过，此时整张图\(20\)个点所能表示的数字范围为\([0,2^{19}-1=524287]\)，无法满足\(L=1000000\)的情况

前面提及：

• 如果只考虑第\(1\)个点到第\(i\)个点，其所能表示出的数字范围为\([0,2^{i-1}-1]\)

而如果给这个范围加上一个常数\(a\)，就变得能够表示\([a,a+2^{i-1}-1]\)内的数字了

假设此前我们所能表示出的数字为\([0,limit-1]\)，以\(limit\)变量表示此时最小的不能表示出的数字

以\(limit\)变量作为常数，那就可以将\([limit,limit+2^{i-1}-1]\)之内的数字表示出来了

换在构造的有向图中，这也就表示自第\(i\)个点向第\(n\)个点连一条权值为\(limit\)的边

建边后，\(limit\)也就变成了\(limit+2^{i-1}\)

下图表示\(L=74\)（边权和范围为\([0,73]\)）所构造出的有向图：

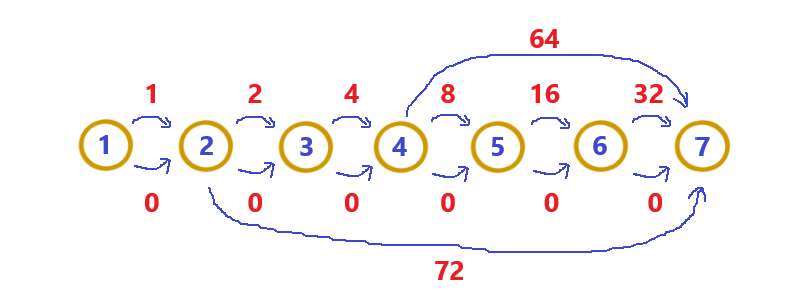
第三部分

上述方法实际上也就是考虑\(L-limit\)的二进制表示法上\(1\)所在的位置，并将其与终点连边

所以需要让\(i\)从大到小遍历去判断是否第\(1\)个位置到第\(i\)个位置所能表示的数字数量（\(2^{i-1}\)）小于剩余的不能表示出的数字数量\((L-limit)\)

因此，本题只需要循环遍历两遍即可，具体实现方式详见代码部分

本思路点数\(n\)最多为\(20\)，边数最多为\((20-1)*2+19\leq 60\)，满足题意

程序

#include<bits/stdc++.h>
using namespace std;

struct node
{
    int u,v,w;
    node(){}
    node(int u,int v,int w):u(u),v(v),w(w){}
};
vector<node> ans;
int L,mx,sum[25];

int main()
{
    scanf("%d",&L);
    L--;
    
    sum[1]=0;
    for(int i=1;i<=20;i++)
    {
        sum[i+1]=sum[i]+(1<<(i-1)); //到第i+1个点所能表示出的最大数字
        if(sum[i+1]<=L) //如果在L-1的范围内
        {
            ans.push_back(node(i,i+1,1<<(i-1))); //两点间进行2的次方幂连边
            ans.push_back(node(i,i+1,0)); //不选
            mx=i+1;
        }
        else
            break;
    }
    
    int limit=sum[mx]+1; //limit用于表示此时最小的不能表示出的数字
    for(int i=mx;i;i--)
    {
        if(sum[i]<=L-limit) //如果连一条limit的边，不会超出范围
        {
            ans.push_back(node(i,mx,limit));
            limit+=sum[i]+1; //注意+1
        }
    }
    
    printf("%d %d\n",mx,ans.size());
    for(node &nd:ans)
        printf("%d %d %d\n",nd.u,nd.v,nd.w);
    
    return 0;
}