2020杭电多校 3H / HDU 6798 - Triangle Collision (平面几何/二分)
题意
有一小球在一个边长为\(L\)的等边三角形内运动
其拥有一个初始位置\((x,y)\)以及恒定速度\((V_x,V_y)\)
询问当第\(k\)次撞击三角形边缘时花费的时间
保证小球在前\(k\)次撞击不会撞到三角形的某个角
思路
先放一篇学长的博客《Triangle Collision(二分 平面几何)》 JK Chen写得很清晰,我也是看完后才换了想法过的这题
实际上如果我们可以不把小球的碰撞当作一种平面反射,而是把整个平面视作是由无限个等边三角形组合而成的
于是我们就能够把平面看作是由无数条\(y=b,\ y=\sqrt 3x+b,\ y=-\sqrt 3x+b\)这三类直线组成的
每类直线两两之间距离\(\frac {\sqrt 3}{2}L\),且三类直线各有一条线交于三角形的顶点
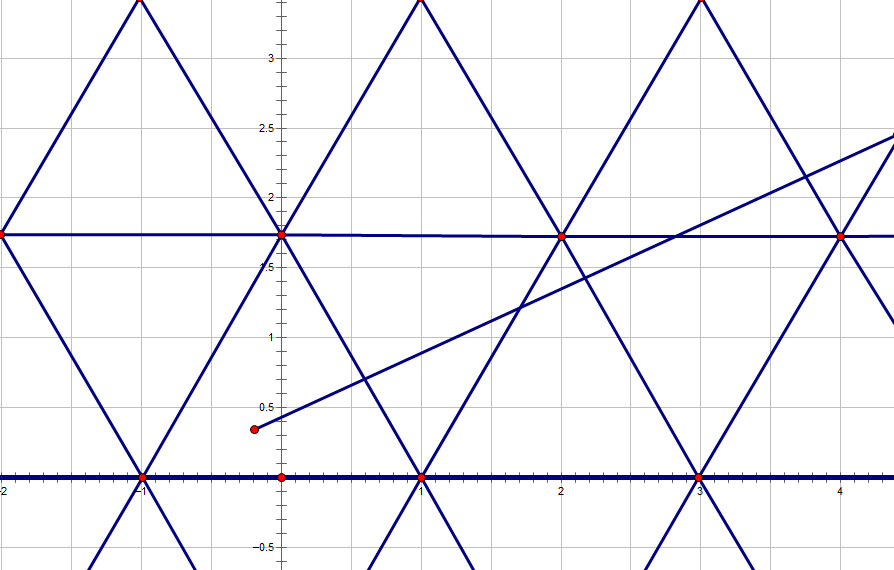
假设我们知道了终点,那么碰撞次数也就等同于起点到终点这条线段与图中三类直线的交点个数
于是我们可以想到,尝试二分距离或者是时间,计算出终点后判断即可
那么问题就变成了线段与平面内直线的交点个数
既然已经将直线分成三类了,那就可以一类一类地去求交点个数
考虑根据三类直线重新选取坐标系
如果选择形如\(y=b\)直线的坐标系,略去其余两类直线后,平面内将只剩下下图所示
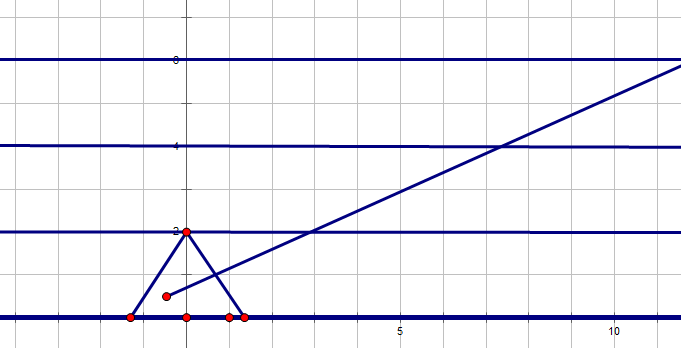
此时,终点与起点的\(y\)轴差值\(\Delta y\)加上起点的\(y\)轴值\(y_0\)与三角形高度\(h\)的整除结果\(\frac {\Delta y+y_0}{h}\)就是这条线段与直线\(y=b\)类的交点个数
如果线段往\(y-\)方向移动
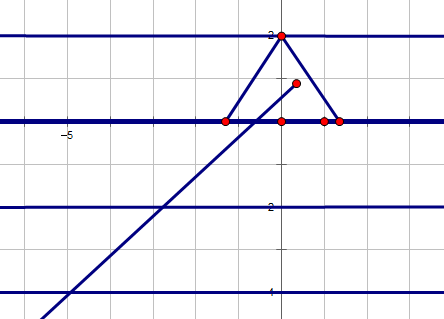
此时,\(\frac {\Delta y-y_0}{h}+1\)是这条线段与直线\(y=b\)类的交点个数
如果转换了坐标系,那么我们可以拿初始的三角形的边作为底边(新坐标系的\(x\)轴),用相同的处理方式求出交点个数
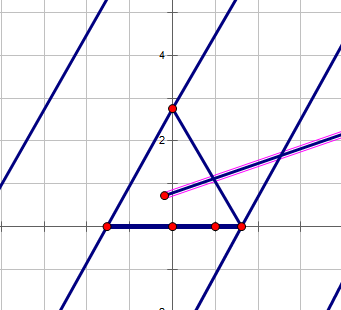
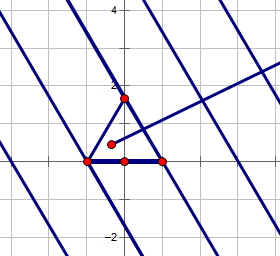
三种情况的交点个数和即为该条线段的交点个数
完整程序
各种坐标系对应的底边最好画图观察下
旋转后的向量对应的坐标系也最好画图看下
(感觉关键就在于旋转)
(343ms/2000ms)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const double eps=1e-12;
const double PI=acos(-1.0);
int dbcmp(double x){
if(fabs(x)<eps)
return 0;
return x<0?-1:1;
}
struct Point{
double x,y;
Point(){}
Point(double _x,double _y){
x=_x;
y=_y;
}
bool operator == (Point b)const{
return dbcmp(x-b.x)==0&&dbcmp(y-b.y)==0;
}
Point operator -(const Point &b)const{ //叉积
return Point(x-b.x,y-b.y);
}
double operator ^(const Point &b)const{ //点积
return x*b.y-y*b.x;
}
double operator *(const Point &b)const{
return x*b.x+y*b.y;
}
Point operator +(const Point &b)const{
return Point(x+b.x,y+b.y);
}
Point operator *(const double &k)const{
return Point(x*k,y*k);
}
Point operator /(const double &k)const{
return Point(x/k,y/k);
}
double distance(Point p){
return hypot(x-p.x,y-p.y);
}
Point Rotate(double rad){ //逆时针旋转
return Point(x*cos(rad)-y*sin(rad),x*sin(rad)+y*cos(rad));
}
};
struct Line{
Point s,e;
Line(){}
Line(Point _s,Point _e){
s=_s;
e=_e;
}
bool pointonseg(Point p){
return dbcmp((p-s)^(e-s))==0&&dbcmp((p-s)*(p-e))<=0;
}
double getDistance(Point A){ //点到直线的距离
return fabs((A-s)^(A-e)/s.distance(e));
}
Point crosspoint(Line v){
double a1=(v.e-v.s)^(s-v.s);
double a2=(v.e-v.s)^(e-v.s);
return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1));
}
};
const double sq3=sqrt(3);
double L,x,y,vx,vy,h;
int k;
Point A,B,C,oripot,v1,v2,v3;
Line AB,AC,BC;
bool check(double tim)
{
ll kk=0;
double dis;
dis=BC.getDistance(oripot)+v1.y*tim; //第一种坐标系对应边BC,计算出起点高度+y轴经过距离Δy
if(dis<0)
kk+=(ll)((-dis)/h)+1; //如果方向为负方向,计算结果与直接整除略有不同
else
kk+=(ll)(dis/h); //正方向正常整除
dis=AC.getDistance(oripot)+v2.y*tim; //第一种坐标系对应边AC,计算出起点高度+y轴经过距离Δy
if(dis<0)
kk+=(ll)((-dis)/h)+1;
else
kk+=(ll)(dis/h);
dis=AB.getDistance(oripot)+v3.y*tim; //第一种坐标系对应边AB,计算出起点高度+y轴经过距离Δy
if(dis<0)
kk+=(ll)((-dis)/h)+1;
else
kk+=(ll)(dis/h);
return kk>=k; //最后判断当前的交点个数是否大于等于要求的个数
}
void solve()
{
cin>>L>>x>>y>>vx>>vy>>k;
h=sq3*L/2.0; //三角形高度
v1=Point(vx,vy); //第一种坐标系下的速度向量
v2=v1.Rotate(PI*2.0/3); //第二种坐标系下的速度向量(逆时针旋转120°)
v3=v1.Rotate(-PI*2.0/3); //第三种坐标系下的速度向量(顺时针旋转120°)
oripot=Point(x,y); //小球初始位置
A=Point(0,h); //三角形上角
B=Point(L/2.0,0); //三角形右角
C=Point(-L/2.0,0); //三角形左角
AB=Line(A,B); //三条边组成的线
AC=Line(A,C);
BC=Line(B,C);
double l=0,r=1e10,mid; //二分时间,计算交点个数是否符合条件
while(r-l>=1e-5) //题目不卡精度,实测1e-4也能过
{
mid=(l+r)/2.0;
if(check(mid))
r=mid;
else
l=mid;
}
cout<<r<<'\n';
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cout<<fixed<<setprecision(8);
int T;cin>>T;
for(int t=1;t<=T;t++)
solve();
return 0;
}


