Codeforces 1359C - Mixing Water （数学）

Educational Codeforces Round 88 (Rated for Div. 2) - C

题意

拥有无数杯冷水无数杯热水，热水温度为 h ，冷水温度为 c

从热水开始，每次交替 热水-冷水 倒入另一个盆中

盆中水的温度为倒入的水温平均值

问最少倒几次能使得盆中水的温度最接近于 t

限制

Time limit per test: 2 seconds

Memory limit per test: 256 megabytes

1≤T≤3⋅10⁴

1≤c<h≤10⁶ ; c≤t≤h

解题思路

从热水开始，每次交替倒入盆中

可以发现如果倒的次数为偶数次，那么盆中水温一定为冷热水的平均值 (h+c)/2 ，令这个平均值为 mid

而如果倒的次数为奇数次，那么盆中水温将随着倒的次数的增多，从 h 开始往 mid 靠拢

得到如下图示

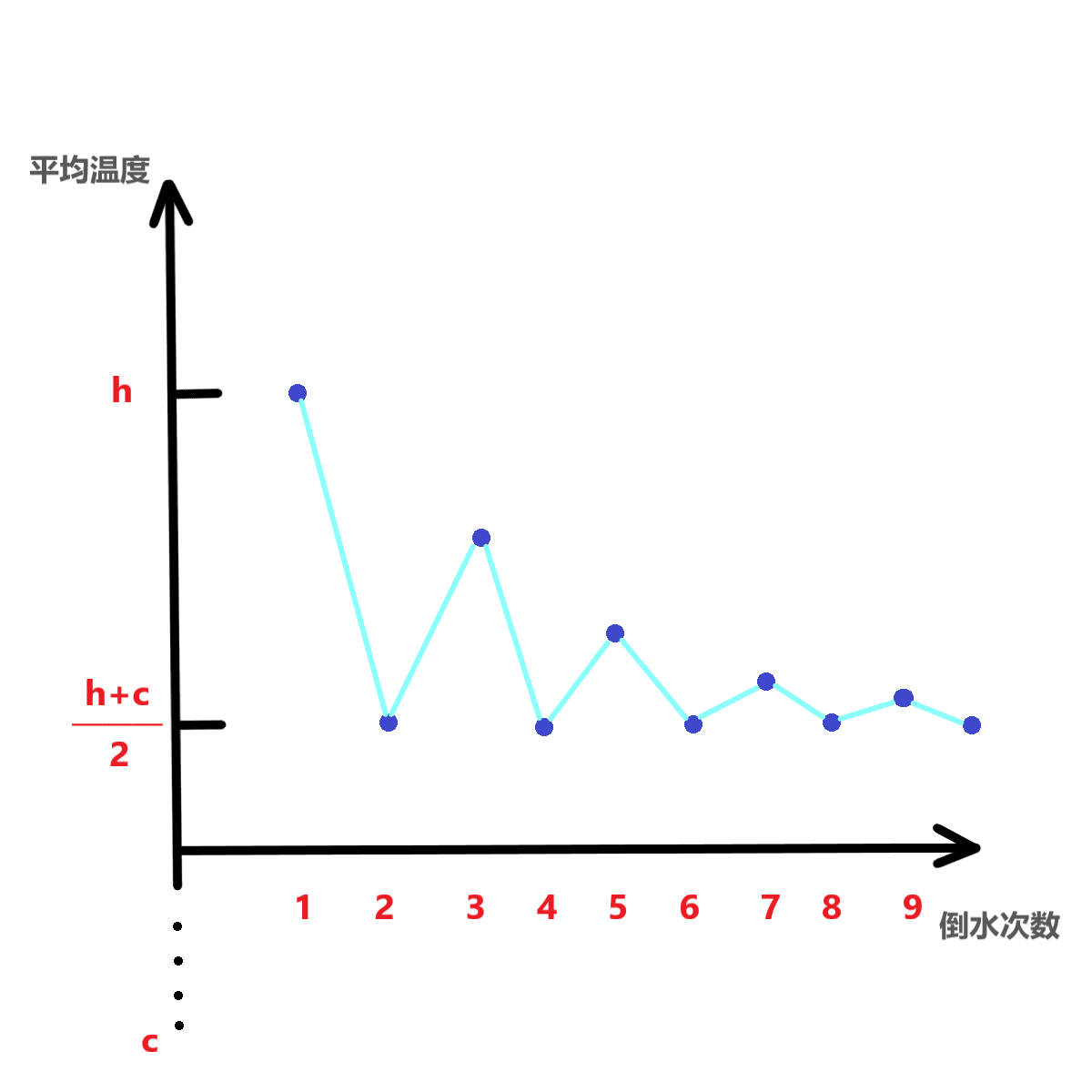
所以首先得出两个特判

如果 t==h 输出 1

如果 t<=mid 输出 2

剩余的，即 mid<t<h 的部分，首先可以得到他们需要的倒水次数一定是奇数

且如果倒水次数从 1 开始，按照 1 3 5 7 ... 的顺序计算水温

则肯定会有某一次操作 x 使得水温 >= t ，且第 x+2 次操作使得水温 < t

但是从 1 开始每次 +2 枚举，配合上数据组数会导致超时

所以还是要从公式入手

可以得到，如果操作次数为偶数次，则平均水温一定为 mid

但此时答案操作次数为奇数次，令答案为 ans

则操作 ans-1 次时，得到水温总和为 (ans-1)*mid

第 ans 次加入的是热水 h

所以可以得到如下公式

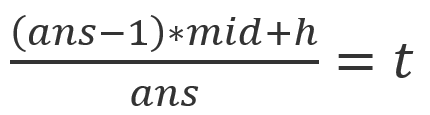
移项得

所以可以得到答案的近似操作次数

由于操作次数一定是个整数，所以可以在求出此时的 ans 后，在 ans 周围枚举判断下哪一次操作才是真正的答案

计算误差不会太大，所以在 ±3 范围内查找即可

完整程序

#include<bits/stdc++.h>
using namespace std;

void solve()
{
    double h,c,t,mid;
    cin>>h>>c>>t;
    mid=(h+c)/2.0;
    
    if(h==t)
    {
        cout<<1<<'\n';
        return;
    }
    if(mid>=t)
    {
        cout<<2<<'\n';
        return;
    }
    
    int d=(mid-h)/(mid-t),ans,i;
    double delta=1e8,tmp;
    
    i=max(1,d-3); //最小值不能小于 1
    if(i%2==0)
        i--; //必须是奇数
    for(;i<=d+3;i+=2)
    {
        tmp=fabs(1.0*((i-1)*mid+h)/i-t); //计算操作i次的水温差值
        if(tmp<delta)
        {
            delta=tmp;
            ans=i;
        }
    }
    
    cout<<ans<<'\n';
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int T;cin>>T;
    while(T--)
        solve();
    return 0;
}