【数据结构】倍增算法(在线) - 树上最近公共祖先
倍增算法
倍增算法采用了二分缩小范围的思想
使得待求两节点持续跳跃2的次方级的距离来快速求出LCA
是常见的求树上节点LCA的在线算法
倍增算法是要让同深度的两个节点同时向根节点方向跳跃
直到第一次在同一个祖先节点遇到
那么这个祖先节点就是他们的最近公共祖先节点LCA
在跳跃的过程中,每次跳跃的步数为2的次方
如果会跳到根节点及以上(当然不存在)(即步数大于等于深度),则不能跳
或者两节点跳跃后的位置相同,说明可能已经跳过了LCA(或者这个节点就是LCA),难以处理,不能跳
跳跃停止的条件是与两节点相邻的父节点是同一节点,即此时两个位置为LCA的子节点时
在一棵n个节点的树上
预处理时间复杂度为 O(nlogn)
询问时间复杂度为 O(logn)
总体复杂度为 O((n+q)logn)
倍增算法的实现方式
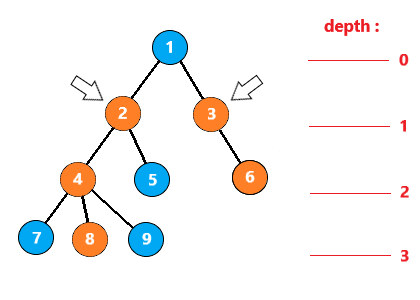
假设我们现在拥有下面这样一棵树
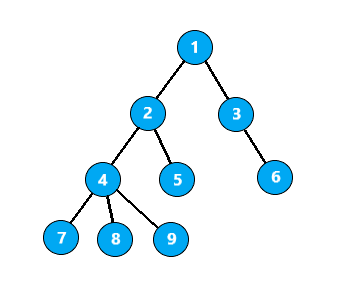
询问节点6与节点8的LCA
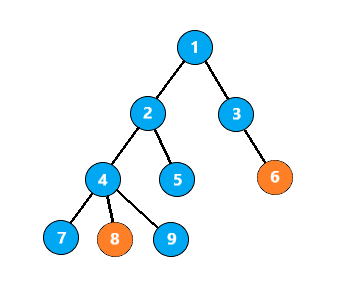
首先要使得待求的两节点深度相同,让深度大的节点跳到与深度小的节点相同深度的祖先节点位置
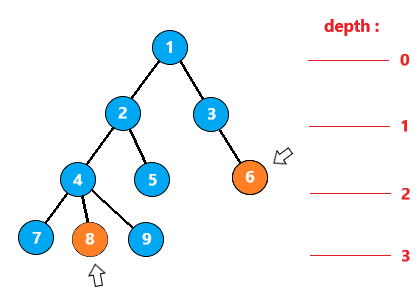
然后开始从大到小枚举2的次方倍步数,这里从3开始枚举
如果两节点同时向上移动23=8步,大于节点深度,所以不能跳
如果两节点同时向上移动22=4步,大于节点深度,也不能跳
如果两节点同时向上移动21=2步,此时是恰好等于节点深度的,说明跳跃后两节点会都到根节点的位置,也是不能跳的
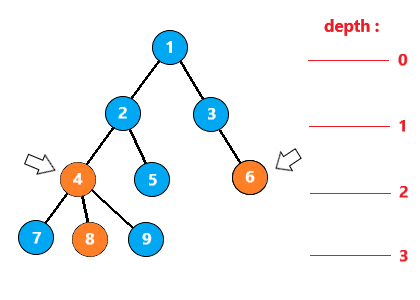
最后,如果两节点同时向上移动20=1步,发现跳跃后的节点是不同的(4->2 , 6->3),所以进行跳跃
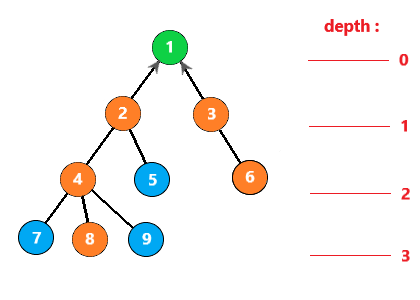
发现此时2和3的父节点是相同的,所以可以直接返回这个父节点,说明找到了LCA
代码实现
模拟数据给定方式
第一行给出三个数n m q,表示有n个节点,m条边,q次询问 (假设此时n,q<=10000)
接下来m行,每行两个数a b (1≤a,b≤n , a≠b),表示这两个节点之间存在一条边
接下来q行,每行两个数a b (1≤a,b≤n),询问LCA(a,b)
数据储存方式
const int MAXN=10050,MAXF=16;// MAXF>log2(MAXN)
vector<int> G[MAXN];//存图
int depth[MAXN];//点深度
int father[MAXN][MAXF];//[i][j]为第i个点的距离为2^j的祖先
bool vis[MAXN];//访问标记
这里的MAXF应该大于可能的最大步数对2取对数后的值
用于申请father数字空间以及后面枚举步数时的最大范围
输入数据的处理与调用
int main()
{
int n,m,q,a,b;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
G[a].push_back(b);
G[b].push_back(a);//双向存边
}
dfs(1,0);//从节点1开始深搜处理father数组与depth数组,令1的父节点为0
while(q--)
{
scanf("%d%d",&a,&b);
printf("%d\n",lca(a,b));
}
return 0;
}
※dfs处理与每个节点存在指数关系的father以及深度depth
void dfs(int pos,int fa)
{
vis[pos]=true;//标记访问
depth[pos]=depth[fa]+1;//深度为相邻父节点深度+1
father[pos][0]=fa;//2^0=1,所以第0层父节点直接指向相邻父节点
for(int i=1;i<MAXF;i++)
father[pos][i]=father[father[pos][i-1]][i-1];
int cnt=G[pos].size();
for(int i=0;i<cnt;i++)
{
if(!vis[G[pos][i]])
dfs(G[pos][i],pos);//往子树深搜
}
}
假设与u距离25=32步的祖先节点为v
那么与u距离26=64步的祖先节点,也就是与v距离25=32步的祖先节点
又因为深度优先搜索,所以一旦搜索到某个节点u
也就代表着它的所有祖先都已经被搜索并处理过
此时就能直接获得迭代关系 father[u] [i] = father[v] [i-1]
此时u=pos , v=father[pos] [i-1]
所以关系为 father[pos] [i] = father[ father[pos] [i-1] ] [i-1]
※求出最近公共祖先LCA
int lca(int a,int b)
{
while(depth[a]<depth[b])//如果b的深度比a大
{
for(int i=MAXF-1;i>=0;i--)
{
if(depth[b]-(1<<i)>=depth[a])//如果b跳2^i步后深度大于等于a,则可以进行跳跃
b=father[b][i];
}
}
while(depth[a]>depth[b])//如果a的深度比b大
{
for(int i=MAXF-1;i>=0;i--)
{
if(depth[a]-(1<<i)>=depth[b])//同上,如果a跳2^i步后深度大于等于b,则可以进行跳跃
a=father[a][i];
}
}
if(a==b)//处理完深度后,如果ab为同一节点,说明原本就在同一条边上,此时直接返回即可
return a;
while(father[a][0]!=father[b][0])//如果与ab相邻的父节点不是同一个节点,说明还需要继续寻找下去
{
for(int i=MAXF-1;i>=0;i--)
{
if(father[a][i]!=father[b][i])//如果跳跃2^i步到达的祖先节点不同的话才能跳跃
{
a=father[a][i];
b=father[b][i];
}
}
}
return father[a][0];//返回此时相邻的父节点作为LCA
}
首先是对于深度的处理,同样借助于father数组,从大到小枚举次方,每次跳2的次方步判断是否会跳过深度较小的节点深度。如果深度仍然大于等于深度较小的节点,则进行跳跃直到深度相等。
如果原本两节点位于同一条边上(例如上图中的2和7)
或者输入时a与b就是相同的(我将其称作明知故问)
那么经过第一步处理后a==b就成立了
此时可以直接返回a或b作为LCA
否则,就需要同时让两节点进行跳跃来查找
相同的,从大到小枚举次方
因为此前搜索时令根节点1的父节点为0
所以如果步数太大跳过了根节点1的话,father数组就会全部置0
所以不需要处理太多情况
当步数太大以至于跳过根节点时,father[a][i] == father[b][i] == 0 成立
当跳跃后两节点相同时,father[a][i] == father[b][i] 成立
所以所有不可取的情况都可以通过这么一句处理掉
最后得到的可以进行跳跃的条件就是 father[a][i] ≠ father[b][i]
最后,输出a或者b的相邻父节点作为LCA即可
至此,倍增算法就算实现了
完整代码(模板)
#include<bits/stdc++.h>
using namespace std;
const int MAXN=10050,MAXF=16;
vector<int> G[MAXN];
int depth[MAXN];
int father[MAXN][MAXF];
bool vis[MAXN];
void dfs(int pos,int fa)
{
vis[pos]=true;
depth[pos]=depth[fa]+1;
father[pos][0]=fa;
for(int i=1;i<MAXF;i++)
father[pos][i]=father[father[pos][i-1]][i-1];
int cnt=G[pos].size();
for(int i=0;i<cnt;i++)
{
if(!vis[G[pos][i]])
dfs(G[pos][i],pos);
}
}
int lca(int a,int b)
{
while(depth[a]<depth[b])
{
for(int i=MAXF-1;i>=0;i--)
{
if(depth[b]-(1<<i)>=depth[a])
b=father[b][i];
}
}
while(depth[a]>depth[b])
{
for(int i=MAXF-1;i>=0;i--)
{
if(depth[a]-(1<<i)>=depth[b])
a=father[a][i];
}
}
if(a==b)
return a;
while(father[a][0]!=father[b][0])
{
for(int i=MAXF-1;i>=0;i--)
{
if(father[a][i]!=father[b][i])
{
a=father[a][i];
b=father[b][i];
}
}
}
return father[a][0];
}
int main()
{
int n,m,q,a,b;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
G[a].push_back(b);
G[b].push_back(a);
}
dfs(1,0);
while(q--)
{
scanf("%d%d",&a,&b);
printf("%d\n",lca(a,b));
}
return 0;
}
以HDU2586为例
#include<iostream>
#include<utility>
#include<vector>
using namespace std;
typedef pair<int,int> P;
const int MAXN=40050,MAXF=18;
vector<P> G[MAXN];//first存id,second存距离
int depth[MAXN];
int father[MAXN][MAXF];
int dis[MAXN];//与根节点距离
bool vis[MAXN];
void dfs(int pos,int fa)
{
vis[pos]=true;
depth[pos]=depth[fa]+1;
father[pos][0]=fa;
for(int i=1;i<MAXF;i++)
father[pos][i]=father[father[pos][i-1]][i-1];
int cnt=G[pos].size();
for(int i=0;i<cnt;i++)
{
if(!vis[G[pos][i].first])
{
dis[G[pos][i].first]=dis[pos]+G[pos][i].second;//先处理子节点的dis
dfs(G[pos][i].first,pos);
}
}
}
int lca(int a,int b)
{
while(depth[a]<depth[b])
{
for(int i=MAXF-1;i>=0;i--)
{
if(depth[b]-(1<<i)>=depth[a])
b=father[b][i];
}
}
while(depth[a]>depth[b])
{
for(int i=MAXF-1;i>=0;i--)
{
if(depth[a]-(1<<i)>=depth[b])
a=father[a][i];
}
}
if(a==b)
return a;
while(father[a][0]!=father[b][0])
{
for(int i=MAXF-1;i>=0;i--)
{
if(father[a][i]!=father[b][i])
{
a=father[a][i];
b=father[b][i];
}
}
}
return father[a][0];
}
void solve()
{
int n,q,a,b,d;
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)
{
G[i].clear();
vis[i]=false;
}//因为其余数组都是直接覆盖的,没有引用前一次的值,所以不需要初始化
for(int i=1;i<n;i++)
{
scanf("%d%d%d",&a,&b,&d);
G[a].push_back(P(b,d));
G[b].push_back(P(a,d));
}
dfs(1,0);
while(q--)
{
scanf("%d%d",&a,&b);
printf("%d\n",dis[a]+dis[b]-2*dis[lca(a,b)]);
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
solve();
return 0;
}


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步