【数据结构】线段树 - 定义 & 点修改/区间求和
线段树
本文描述高级数据结构线段树的定义,并解决 点修改/区间求和 的问题
结构与定义
线段树的基本结构
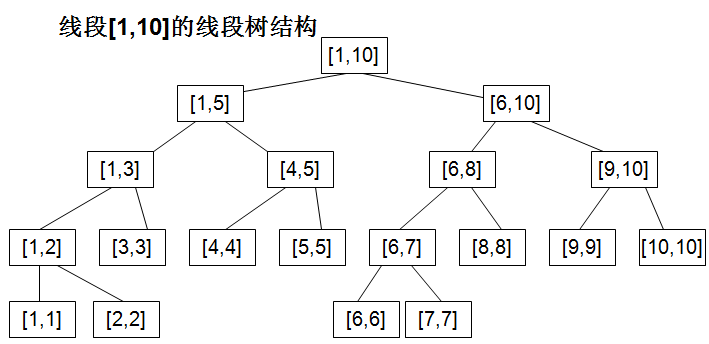
由图可知,线段树的每一个节点都代表着一段区间
且同一层的节点(深度相同的节点)所表示的区间互不重叠
所有叶子节点代表的区间左边界与右边界相同(叶子节点代表单个元素)
普遍规定
如果某个非叶子节点代表的区间包含元素个数为奇数
则它的左儿子包含的元素个数比右儿子大 1
在代码部分,非叶子节点表示区间为 [l,r]
则左儿子为 [ l , (l+r)/2 ] ,右儿子为 [ (l+r)/2+1 , r ]
除法计算向下取整
如果需要用线段树对一段包含N个数的区间操作,则树一般需要开4N的空间以避免越界
存储方式
线段树以数组存储节点的值
以层序遍历的方式自上而下,自左而右依次进行编号
一般从0开始或者从1开始
如果从0开始,则左儿子位置为2k+1,右儿子为2k+2
如果从1开始,则左儿子位置为2k,右儿子为2k+1
本文代码编号从1开始
线段树实现方法演示
该部分图片截自av6835937
首先,对于一个区间大小为10的线段树,它的基本构造如下图所示
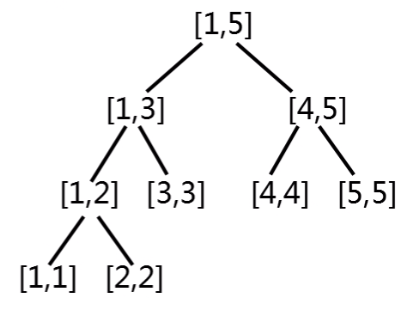
如果区间大小为5,代入一个数组[1,5,4,1,6],那么线段树各个节点表示的元素为
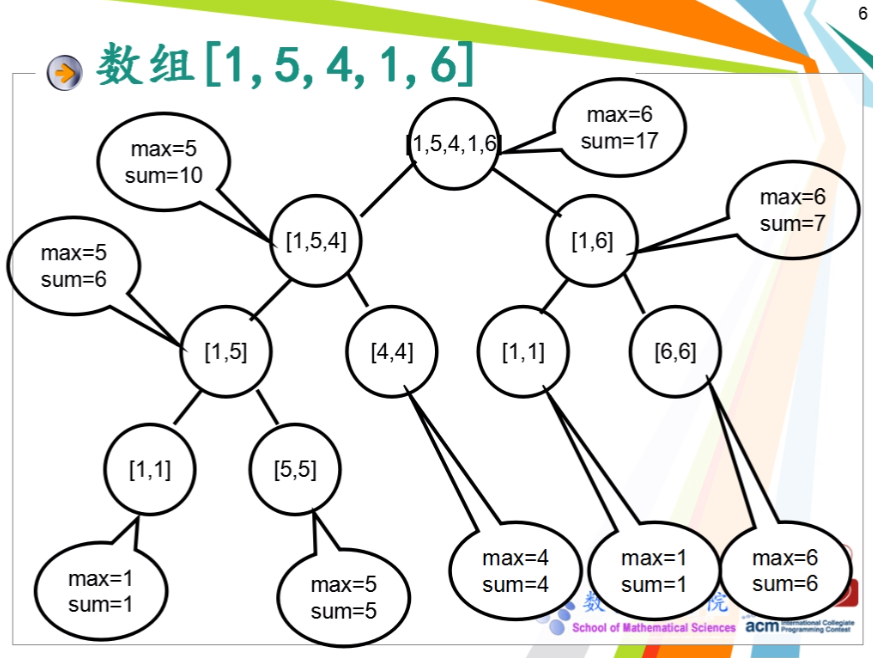
按照上述图示即可先进行建树
然后先考虑点修改的操作
如果要将a[2]的值修改为3,则从根节点到叶子节点的访问顺序为
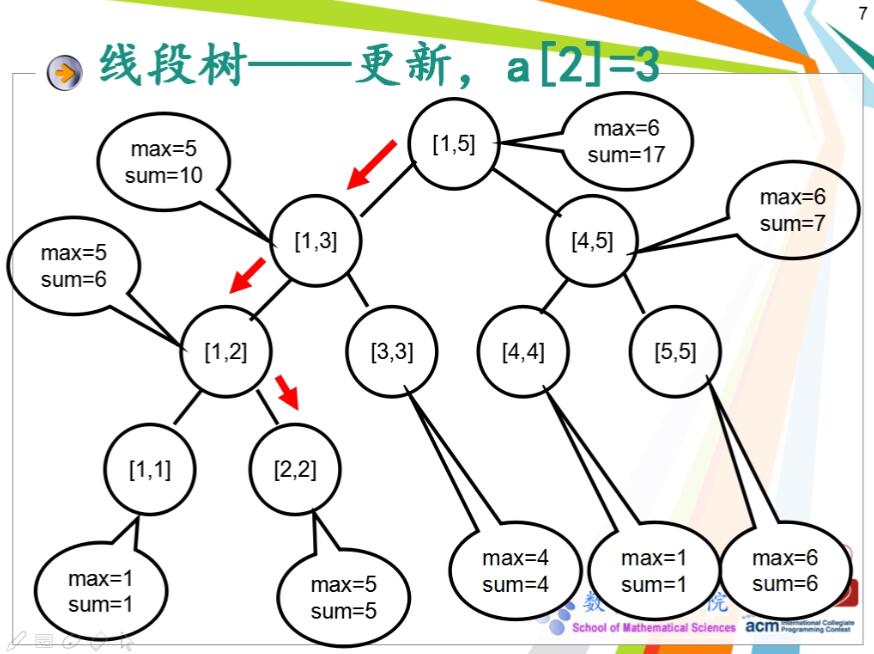
访问到叶子节点后,修改叶子节点的值,然后自下而上回溯每一个访问时经过的节点并依次进行更新,直到回溯到根节点
因为只要叶子节点更新后,它的父节点就可以通过左儿子+右儿子来重新更新sum值,最后完成更新
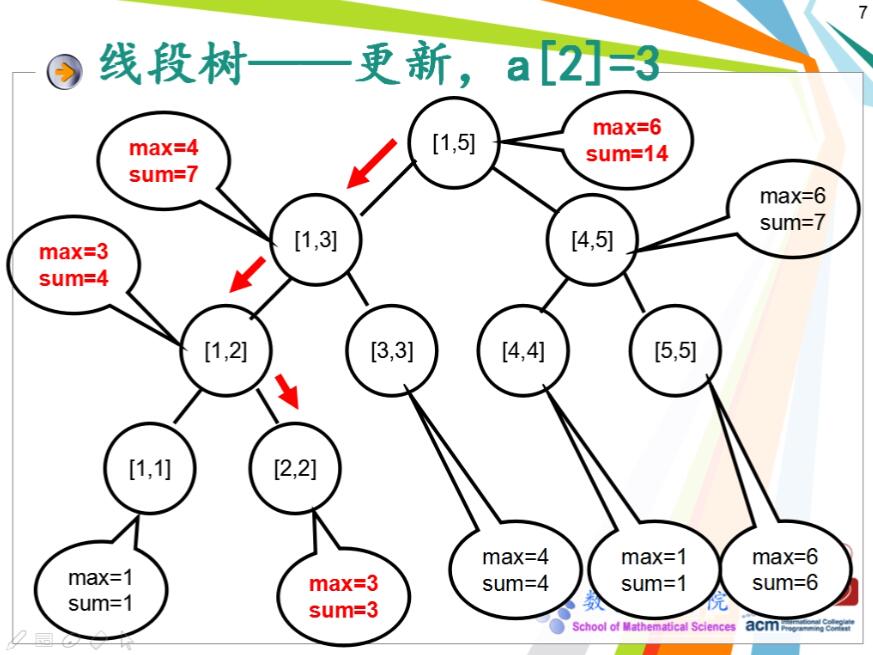
然后考虑区间查询操作
传统方法中,查询区间元素之和的做法就是从[ l , r ]一个个加起来输出,这种O(n)的做法在遇到大数量的查询时运行速度完全无法满足要求
因此,根据线段树的特点,我们可以通过预处理线段的和当作多个元素之和
在上面建树时已经把线段和处理完了,所以接下来就需要考虑把符合的线段按最小个数取出来求和即可
下图展示了求区间[3,5]的和的过程

可以看到,在元素总数为5的线段树里,4 5这两个元素可以用 [4,5] 这个线段来表示
所以3 4 5这三个元素和的值只需要访问[3,3] [4,5]这两个区间就能得到
在查找时,需要以左边界3与右边界5作为媒介
如果访问到的一个节点全部包含于[3,5],那么整个节点就可以直接拿过来作为答案,不需要再访问子树。图中访问到的节点[4,5]就满足这个情况。
如果访问到的一个节点部分包含于[3,5],此时不能拿整个节点的值作为答案,需要分别访问其左子树和右子树。图中的根节点[1,5]与节点[1,3]就满足这个情况。
如果访问到的一个节点不包含于[3,5],则无需继续考虑。图中访问到的节点[1,2]就满足这个情况。(在代码实现部分,这个节点需要访问到,但是因为对答案无贡献所以直接return)
代码实现 - 以点修改/区间求和为例
节点类型的构造 struct node
typedef long long ll;
const int MAXN=1e5+50;
struct node
{
int l,r;
ll sum;
}tree[MAXN*4];
建树 buildTree
int ar[MAXN];
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d",&ar[i]);
buildTree(1,1,n);
void buildTree(int id,int l,int r)
{
tree[id].l=l;
tree[id].r=r;
tree[id].sum=0;
if(l==r)
tree[id].sum=ar[l];
else
{
int mid=(l+r)>>1;
buildTree(id<<1,l,mid);
buildTree(id<<1|1,mid+1,r);
push_up(id);
}
}
按照递归的方法进行建树,main函数读入原数组ar,然后树从编号1开始创建
建树函数传入共三个变量:当前要进行构造的节点id,这个节点代表的区间 l 与 r
因为调用buildTree函数也就相当于tree结构体数组的初始化,所以要记得加tree[id].sum=0这一句
如果当前节点就是叶子节点(即表示的区间的 l 与 r 相同),则直接把sum赋值成对应的ar数组内的值即可
如果是非叶子节点,先获得当前节点表示的区间中间值mid=(l+r)>>1
然后递归左儿子与右儿子建树
这里写法运用了位运算(细微省时)
id<<1 就是把id的二进制全部左移一位,相当于id*2
id<<1|1 就是先把id的二进制全部左移一位,再对1做取或运算,相当于id*2+1
当左儿子与有儿子建树完成时,再更新当前节点的sum值,即push_up函数
更新节点值(向上传递) push_up
void push_up(int id)
{
tree[id].sum=tree[id<<1].sum+tree[id<<1|1].sum;
}
更新节点编号id的sum值为两子节点sum之和
如果子节点发生了改变,则必须更新一遍父节点
所以push_up函数会在建树buildTree和修改节点值update时调用
修改节点值 update
update(1,3,5); //把位置3的值修改为5
void update(int id,int pos,ll val)
{
int L=tree[id].l,R=tree[id].r;
if(L==R&&L==pos){
tree[id].sum=val;
return;
}
if(L<=pos&&pos<=R)
{
int mid=(L+R)>>1;
update(id<<1,pos,val);
update(id<<1|1,pos,val);
push_up(id);
}
}
同样的,update函数需要的三个参数中有一个是迭代参数id,指现在处理的节点id
后两个参数固定不变,故也能修改为全局变量
如果pos正好位于此时节点id表示的线段中,但是id节点不是叶子节点
那么就处理节点id的左右儿子
如果一个节点有被访问到,并且左右儿子都已经访问过了
说明满足条件的那个子节点的值已经成为更新之后的值
此时再更新自己,即push_up(id),然后退出函数,让栈中上一个函数继续执行
这里就是查找路径的回溯,先更新叶子节点再一层层回溯父节点并进行更新
如果满足条件L==R&&L==pos(或等价条件)时,说明此时id指向的是一个叶子节点,并且就是要修改的节点
所以修改后直接return即可,就可以让路径开始回溯,更新父节点
回溯到根节点时,说明这一次update操作就完成了
查询区间和 query
query(1,3,5); //查询区间[3,5]的和
ll query(int id,int l,int r)
{
int L=tree[id].l,R=tree[id].r;
if(l<=L&&R<=r)
return tree[id].sum;
int mid=(L+R)>>1;
ll res=0;
if(mid>=l)
res+=query(id<<1,l,r);
if(mid<r)
res+=query(id<<1|1,l,r);
return res;
}
与update函数类似的迭代
如果满足l<=L&&R<=r,说明当前访问的节点id代表的区间完全包含于查询的区间内
此时直接return tree[id].sum返回id节点的sum值即可
如果节点id代表的区间只是部分包含于查询的区间内
则需要迭代访问两个子节点
如果满足mid>=l,说明节点id的左儿子会部分或全部包含于查询的区间[l,r],则可以用迭代左节点得到的值加入答案
如果满足mid<r,说明节点id的右儿子会部分或全部包含于查询的区间[l,r],则可以用迭代右节点得到的值加入答案
注意这里不能写成mid<=r,因为实际上判断的是mid+1<=r,等价于mid<r
最后返回和加入答案即可
代码调用部分
这一部分采用了例题 HDU1166敌兵布阵 的输入要求:
Add a b 使编号为a的元素值加上b
Sub a b 使编号为a的元素值减去b
Query a b 询问区间[a,b]之和
End 结束程序
char opr[10];
while(1)
{
scanf("%s",opr);
if(opr[0]=='E')
break;
scanf("%d%d",&a,&b);
if(opr[0]=='Q')
printf("%d\n",query(1,a,b));
else if(opr[0]=='A')
update(1,a,b);
else if(opr[0]=='S')
update(1,a,-b);
}
完整程序
#include<iostream>
using namespace std;
typedef long long ll;
const int MAXN=50050;
struct node
{
int l,r;
ll sum;
}tree[MAXN*4];
int ar[MAXN];
void push_up(int id)
{
tree[id].sum=tree[id<<1].sum+tree[id<<1|1].sum;
}
void buildTree(int id,int l,int r)
{
tree[id].l=l;
tree[id].r=r;
tree[id].sum=0;
if(l==r)
tree[id].sum=ar[l];
else
{
int mid=(l+r)>>1;
buildTree(id<<1,l,mid);
buildTree(id<<1|1,mid+1,r);
push_up(id);
}
}
void update(int id,int pos,ll val)
{
int L=tree[id].l,R=tree[id].r;
if(L==R&&L==pos){
tree[id].sum+=val;
return;
}
if(L<=pos&&pos<=R)
{
int mid=(L+R)>>1;
update(id<<1,pos,val);
update(id<<1|1,pos,val);
push_up(id);
}
}
ll query(int id,int l,int r)
{
int L=tree[id].l,R=tree[id].r;
if(l<=L&&R<=r)
return tree[id].sum;
int mid=(L+R)>>1;
ll res=0;
if(mid>=l)
res+=query(id<<1,l,r);
if(mid<r)
res+=query(id<<1|1,l,r);
return res;
}
int main()
{
int T;
scanf("%d",&T);
while(T--){
int i,n;
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d",&ar[i]);
buildTree(1,1,n);
char opr[10];
while(1)
{
scanf("%s",opr);
if(opr[0]=='E')
break;
scanf("%d%d",&a,&b);
if(opr[0]=='Q')
printf("%d\n",query(1,a,b));
else if(opr[0]=='A')
update(1,a,b);
else if(opr[0]=='S')
update(1,a,-b);
}
}
return 0;
}


