机器学习之SVM支持向量机

前言

以下内容是个人学习之后的感悟，转载请注明出处~

简介

　　支持向量机（support vector machine），简称SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特

征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

原理

SVM代价函数

　　支持向量机的代价函数和逻辑回归的代价函数十分相似，因为前者可以从后者中衍化出来。如下图所示，其实，支

持向量机的代价函数只是把逻辑回归的代价函数里的项进行了项替换（这里是相似项，并不对等，从图中可以看出），

并且把1/m去掉了（因为这是无关紧要的）。这时，大家都会觉得奇怪，为什么要替换项呢？替换了之后达到了什么效

果呢？

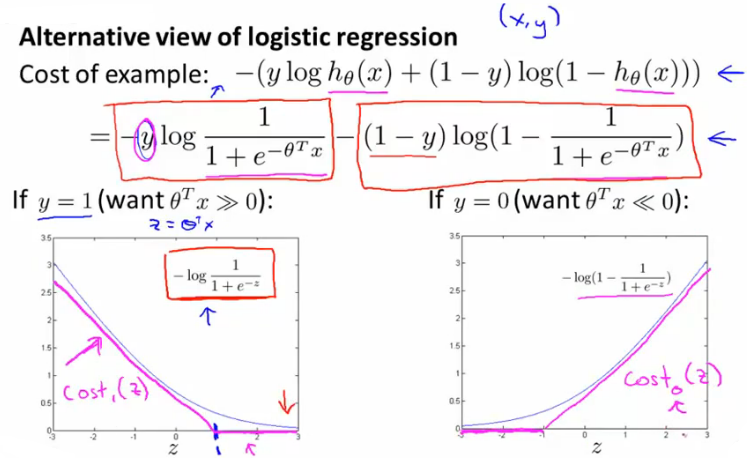
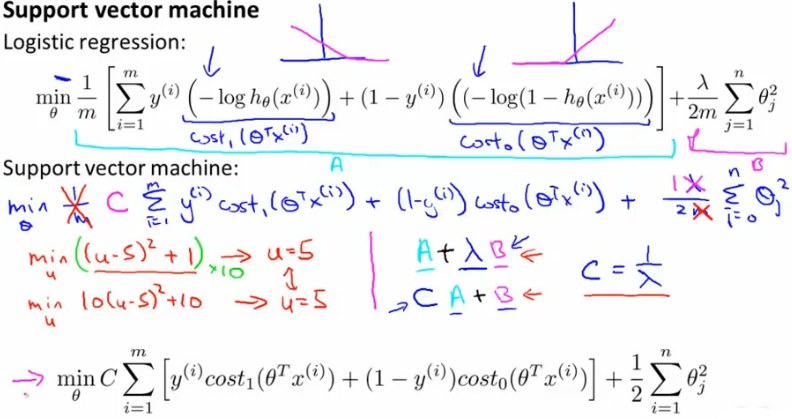
　　事实上，项替换了之后，我们可以在上图清晰地看到，cost₁(z)和cost₂(z)项的曲线图近似于原来逻辑回归中对应项的

曲线，但是这两项比原来更直观，从上图中可以看出，要想最小化代价函数，则：

如果y=1，我们希望θ^Tx≥1；

如果y=0，我们希望θ^Tx≤-1；

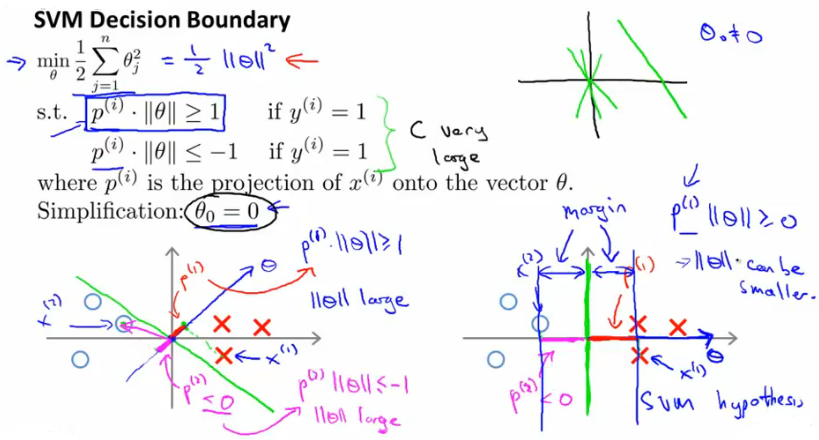
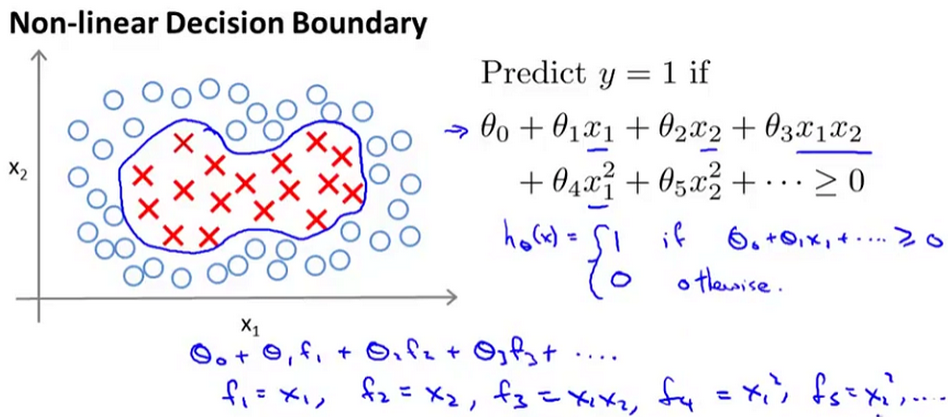
SVM最大间隔超平面

　　首先，介绍一下向量内积，设有两个向量u、v，则u^Tv=p·||u||，其中p为v在u上映射的长度。如下图所示：

　　那么，如何将上面这个数学原理用到SVM中呢？其实很简单，将u，v分别替换为θ、x即可，则θ^Tx=p·||θ||。既然要求

最大间隔，那么只需各个样本特征值的p的值越大，那么超平面（即下图中绿色线）与样本点的间隔越大，分类效果更好。不

过p不能无限制的大，还要满足下图中的约束公式，即p尽量大，θ尽量小，使得代价函数更小，得到最大间隔超平面。

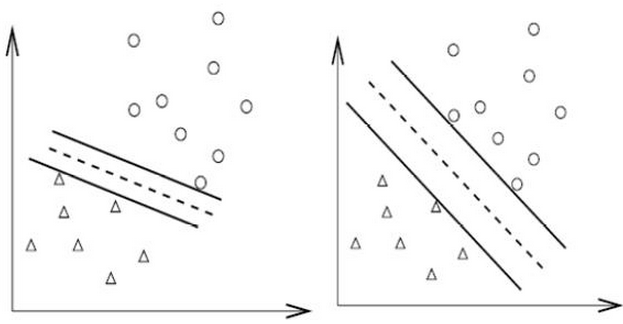
　　接下来，我们看一下SVM分类最大间隔超平面的效果图，下面右图是我们需要的效果，分类效果更加好。

核函数kernels

　　上面都是讲解线性可分的问题，那么，对于线性不可分问题，SVM该如何做呢？对，就是引入核函数，将低维的数据映

射到高维来解决线性不可分问题。目前，常用的核函数有以下几种：

线性核函数（也称无核）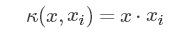
多项式核函数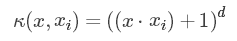
高斯核函数（RBF）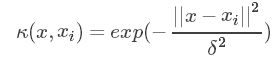
sigmoid核函数

　　那么如何选择核函数呢？本文做以下概述：

如果特征的数量大到和样本数量差不多，则选用LR或者线性核的SVM；
如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；
如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

　　本文将会以较为常见的高斯核函数来讲解核函数在SVM中的作用。下图是

　　我们可以构造一个如上图中所写的多项式特征变量，来区分正负样本。这种多项式还可以写成上图中的： $\theta _{0} + \theta _{1}f_{1} + \theta _{2}f_{2}+....+\theta _{n}f_{n}$ ，

其中 $f_{1} = x_{1},f_{2} = x_{2},f_{3} =x_{1}x_{2},....$ 除了这种表达，还能不能有更好的其他选择去表示特征 $f_{1},f_{2},f_{3},...,f_{n}$ 。这就要引入核函数（kernels），

核函数是一种更好的表达。我们可以通过计算原始向量与landmark之间的相似度来表示特征 $f$ ，如下图所示：

　　当然还可以用其他的函数来计算相似度，只不过这个例子中使用的高斯核函数。我们来看上图中计算 $f_{1},f_{2},f_{3},...$ 的公式，其中：

$f_{1} = similarity(x,l^{(1)}) = exp(-\frac{\left \| x-l^{(1)} \right \|^{2}}{2\sigma ^{2}}) = exp(-\frac{\sum_{j=1}^{n}(x_{j}-l_{j}^{(1)})^{2}}{2\sigma ^{2}})$

因此，我们能够发现：

当 $x\approx l^{(1)}$ 时， $f_{1} \approx exp(-\frac{0^{2}}{2\sigma ^{2}})\approx 1$
当 $x$ 距离 $l^{(1)}$ 很远时， $f_{1} \approx exp(-\frac{(large\ number)^{2}}{2\sigma ^{2}})\approx 0$

　　因此给定一个样本 $x$ 上图中landmark（标记点）会定义出新的特征变量 $\left\{\begin{matrix} l^{(1)}\rightarrow f_{1}\\ l^{(2)}\rightarrow f_{2}\\ l^{(3)}\rightarrow f_{3} \end{matrix}\right.$

　　下面我们来看看根据计算出的特征 $f_{1},f_{2},f_{3},...$ 怎样去分类样本。如下图所示：

　　假设当 $\theta _{0} + \theta _{1}f_{1} + \theta _{2}f_{2} + \theta _{3}f_{3}\geq 0$ 时，我们预测样本类别为“1”，假设我们已经求得 $[\theta _{0}=-0.5,\theta _{1}=1,\theta _{2}=1,\theta _{3}=0]$ ，那

么对于图中给定的样本x，我们可以计算出 $f_{1} \approx 1,f_{2} \approx 0,f_{3} \approx 0$ ，那么代入上式可得： $\theta _{0} + \theta _{1}\cdot 1 + \theta _{2}\cdot 0 + \theta _{3}\cdot 0 = -0.5+1=0.5> 0$ ，

因此预测样本x的类别“1”。因此如果计算大量的样本，就能得出一个非线性的决策边界，如图所示：

　　那么现在有一个问题就是，我们是怎样选择得到 $l^{(1)},l^{(2)},l^{(3)},....$ 的，下面来介绍 $l^{(1)},l^{(2)},l^{(3)},....$ 是如何得到的。

　　在刚开始，我们只需把训练集中的样本一一对应成 $l^{(1)},l^{(2)},l^{(3)},....$ 即可，即给定 $(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),.....,(x^{(m)},y^{(m)})$ ，

令 $l^{(1)} = x^{(1)},l^{(2)} = x^{(2)},.....,l^{(m)} = x^{(m)},$ 如下图所示：

　　因此，若给定一个训练样本 $(x^{(i)},y^{(i)})$ ,能够得到如下特征 $f$ :

$x^{(i)}\rightarrow \left\{\begin{matrix} f_{1} = similarity(x^{(i)},l^{(1)})\\ f_{2} = similarity(x^{(i)},l^{(2)})\\ ...................................\\ f_{m} = similarity(x^{(i)},l^{(m)})\\ \end{matrix}\right.\rightarrow f^{(i)} = \begin{bmatrix} f_{0}^{(i)}\\ f_{1}^{(i)}\\ .\\ .\\ f_{m}^{(i)}\\ \end{bmatrix}$

　　其中 $f_{0}^{(i)} = 1$ 。

　　因此，带核函数的SVM（SVM with kernels）的代价函数变为：

　　关于SVM的核函数（kernels）就介绍到这，下面来看看SVM中参数的选择问题（主要是参数 $C$ 和 $\sigma ^{2}$ 该如何选择）：

实践中使用SVM

　　在实际使用SVM的时候，不建议大家自己实现SVM，因为SVM是一个特定的优化问题。目前已经有非常成熟并且

高度优化的软件包，如国立台湾大学林智仁教授开发的liblinear（http://www.csie.ntu.edu.tw/~cjlin/liblinear/）和LibSVM（http://www.csie.ntu.edu.tw/~cjlin/libsvm/），非常出名。但是我们依然需要做的是以下两点：

以上是全部内容，如果有什么地方不对，请在下面留言，谢谢~

posted @ 2017-08-30 10:55 steed灬阅读(450) 评论(0) 编辑收藏举报

刷新页面返回顶部

steed

The future is in my hands. It's totally up to me.

机器学习之SVM支持向量机

公告