机器学习之梯度下降法
前言
以下内容是个人学习之后的感悟,转载请注明出处~
梯度下降法
一、简介
梯度下降法(gradient decent)是一个最优化算法,通常也称为最速下降法。常用于机器学习和人工智能当中用来递归性地
逼近最小偏差模型。
二、原理
梯度下降法,顾名思义,从高处寻找最佳通往低处的方向,然后下去,直到找到最低点。我们可以看到,J(θ0,θ1)是以θ0,θ1为
自变量的函数,它们的关系如图1中所示。图中,起始点的黑色十字从红色的高坡上,一步一步选择最佳的方向通往深蓝色的低谷,这
其实就是梯度下降法的作用。
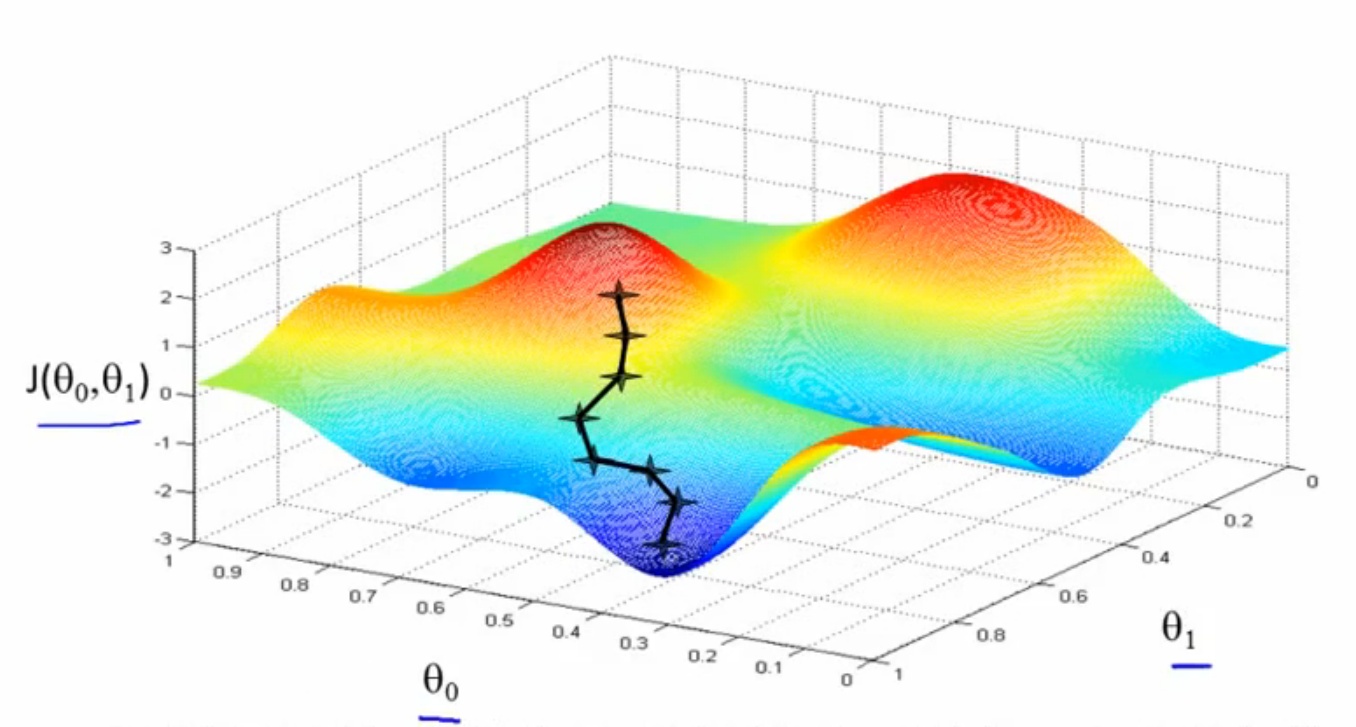
图1
微妙的是图1中的低谷有很多个,选择不同的起始点,最终达到的低谷也会有所不同。如图2所示,黑色十字跑向了另外一个低谷。此时
有些人就会问:为什么会产生这种现象?其实,原因很简单,梯度下降法在每次下降的时候都要选择最佳方向,而这个最佳方向是针对局部
来考虑的,不同的起始点局部特征都是不同的,选择的最佳方向当然也是不同,导致最后寻找到的极小值并不是全局极小值,而是局部极小
值。由此可以看出,梯度下降法只能寻找局部极小值。一般凸函数求极小值时可以使用梯度下降法。
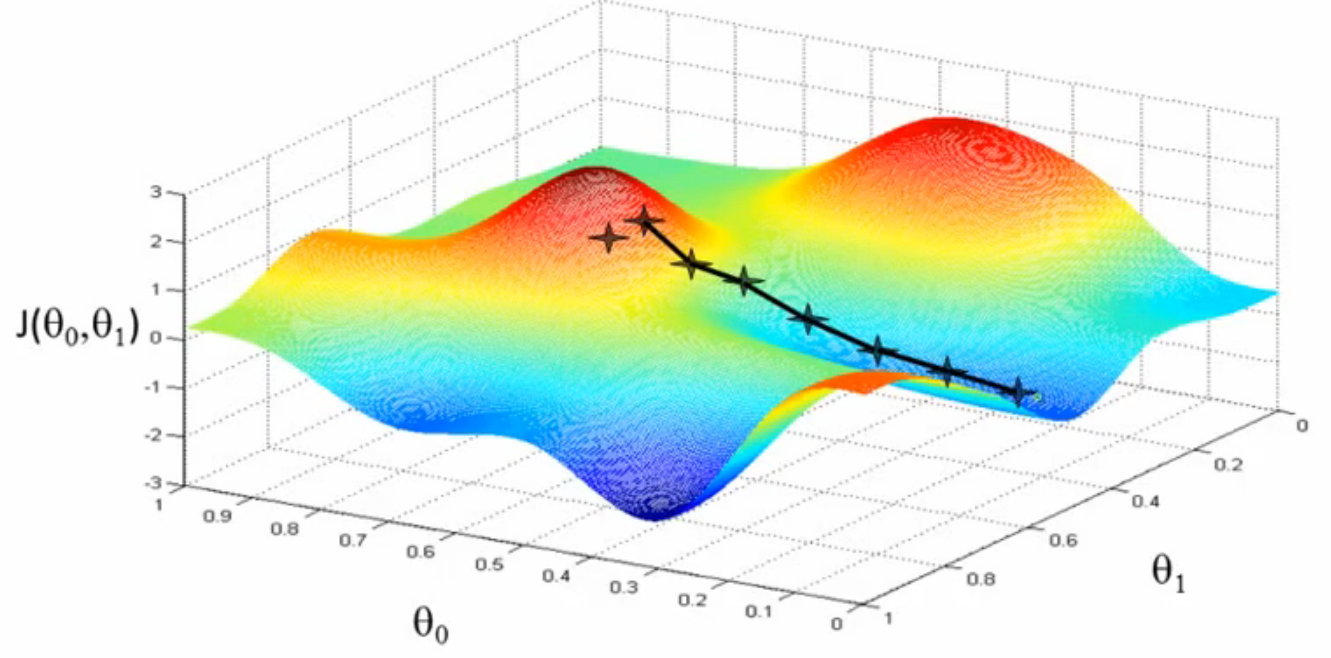
图2
梯度下降法的公式为:
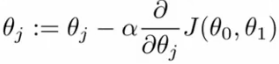 (1)
(1)
公式(1)中“:=”符号代表赋值,并不是代表“等于”,J(θ0,θ1)是需要求极小值的函数。
三、使用方式:以线性回归为例
设线性回归的假设函数为:
![]() (2)
(2)
设代价函数为:
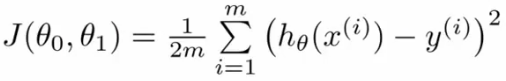 (3)
(3)
目标:寻找J(θ0,θ1)的最小值。
措施:使用梯度下降法:
原理:根据公式(1),可以知道求参数θ,下一步的θ是由上一步的θ减去α乘以J(θ0,θ1)在上一点的斜率值产生的,
如图3所示,然后不断迭代,当θ值不变时,J(θ0,θ1)达到极小值。
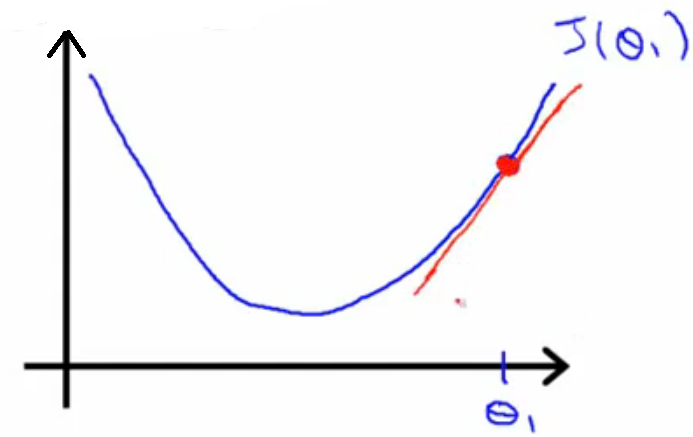
图3
步骤: 不断执行以下公式(4),直到公式(1)收敛,即达到极小值。
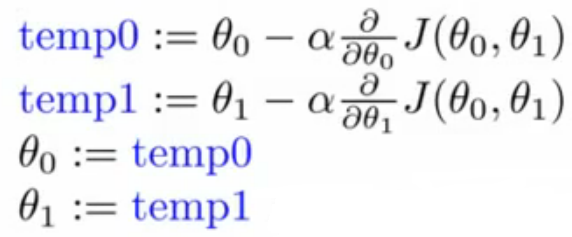
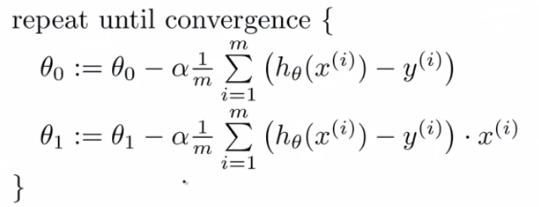 (4)
(4)
注意:公式(4)中各行不能调换顺序,否则并不是梯度下降法(也许是其他算法,如果有哪位大神知道,请不吝赐教~)
比如公式(5)这种形式,θ0刚更新完,马上就用于下一步的θ1的更新计算,脱离了梯度下降法的意图。
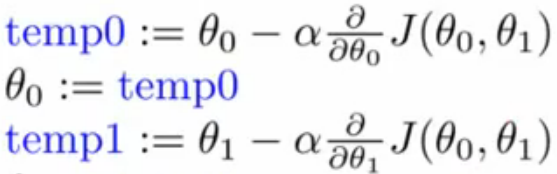 (5)
(5)
四、如何提高梯度下降法的效率
主要有两种方法:
1、特征值x的缩放
why? —— 很多人也许会问:为什么要缩放特征值?缩放特征值x就能提高效率?
本人打算用图4来讲解,J(θ)是假设函数hθ(x)=θ0+θ1x1+θ2x2的代价函数,图中J(θ)关于θ1、θ2的等高线图中带箭头的
红线是迭代的分步,左边是x1、x2数量级相差较大的时候,红线弯来弯去,迭代效率很低,右边则是x1、x2数量级相差较小的时
候,带箭头的红线很快到达了等高线图的最低点,取得极小值,效率很高。所谓的缩放特征值x,就是让所有的x值在数量级
上相差不大,达到提高迭代效率的目的。
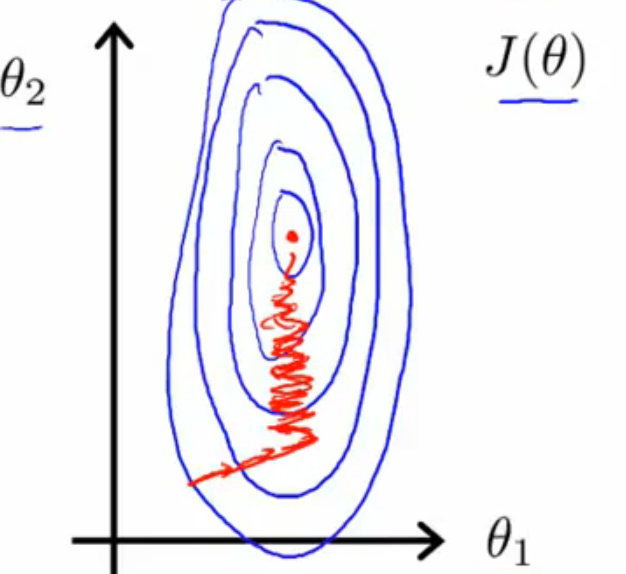
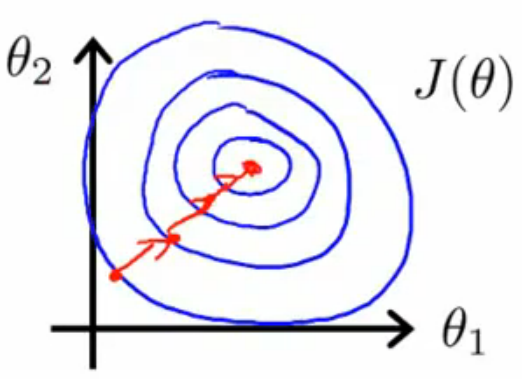
图4
缩放特征值的方法大致有以下三种:
- 除以最大值 (以x1为例,将x1所有样本的值除以max{x1},此时-1≤x1≤1)
- 均值归一化 (x1:=(x1-μ)/(max{x1}-min{x1}),其中μ为x1的平均值,此时-0.5≤x1≤0.5)
- 均值方差归一化
![]()
2、选择适当的α
公式(1)中α起着很重要的作用,如果选的太小,则会出现图5左边这种情况,迭代很慢;如果选的太大,则会出现图4右边这种
情况,很糟糕,过大的α使迭代不收敛。
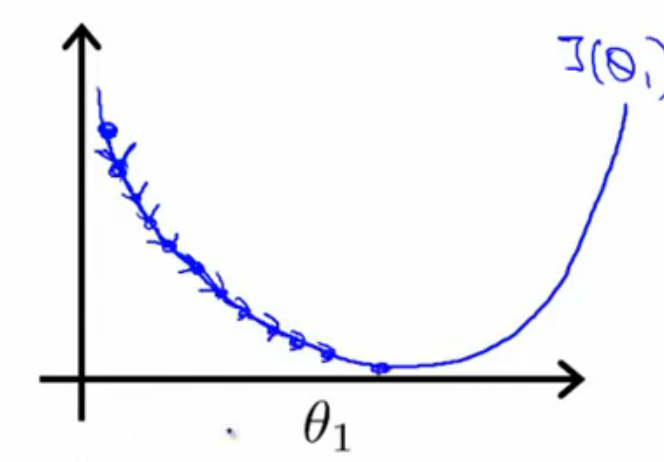
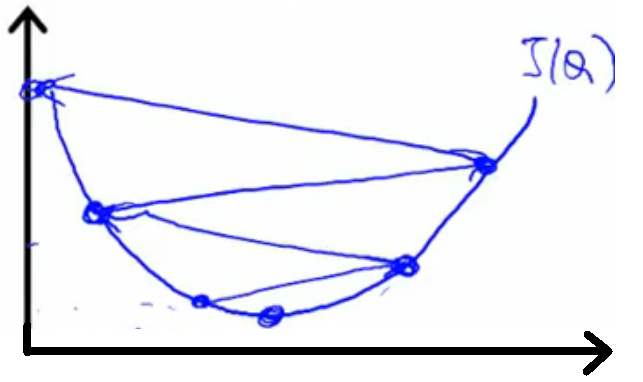
图5
α的选择是需要通过计算一个个试的,按我的经验来说,我一般会这样取值(仅限参考,勿喷~):
- ......,0.001,0.003,0.01,0.03,0.1,.........(以此类推)
以上是全部内容,如果有什么地方不对,请在下面留言,谢谢~


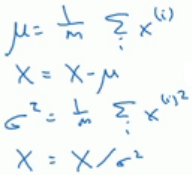

 浙公网安备 33010602011771号
浙公网安备 33010602011771号