新姿势 - 海贼王之伟大航路

Description

“我是要成为海贼王的男人！”，路飞一边喊着这样的口号，一边和他的伙伴们一起踏上了伟大航路的艰险历程。

 

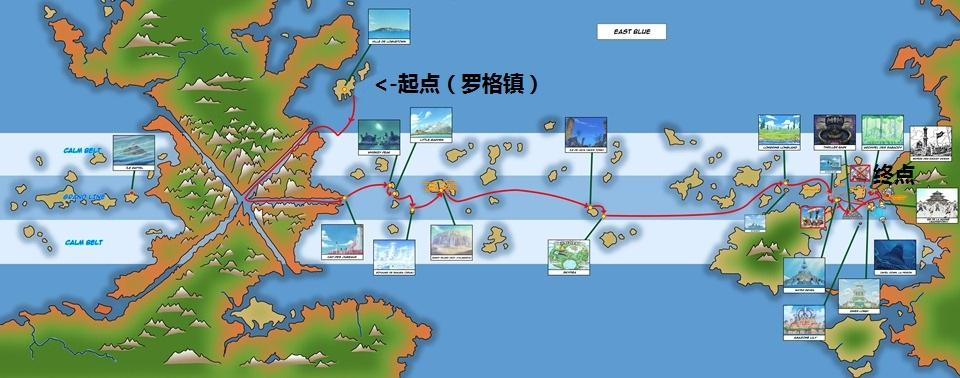
路飞他们伟大航路行程的起点是罗格镇，终点是拉夫德鲁（那里藏匿着“唯一的大秘宝”——ONE PIECE）。而航程中间，则是各式各样的岛屿。

因为伟大航路上的气候十分异常，所以来往任意两个岛屿之间的时间差别很大，从A岛到B岛可能需要1天，而从B岛到A岛则可能需要1年。当然，任意两个岛之间的航行时间虽然差别很大，但都是已知的。

现在假设路飞一行从罗格镇（起点）出发，遍历伟大航路中间所有的岛屿（但是已经经过的岛屿不能再次经过），最后到达拉夫德鲁（终点）。假设他们在岛上不作任何的停留，请问，他们最少需要花费多少时间才能到达终点？

Input

输入数据包含多行。 
第一行包含一个整数N(2 < N ≤ 16)，代表伟大航路上一共有N个岛屿（包含起点的罗格镇和终点的拉夫德鲁）。其中，起点的编号为1，终点的编号为N。 
之后的N行每一行包含N个整数，其中，第i(1 ≤ i ≤ N)行的第j(1 ≤ j ≤ N)个整数代表从第i个岛屿出发到第j个岛屿需要的时间t(0 < t < 10000)。第i行第i个整数为0。

Output

输出为一个整数，代表路飞一行从起点遍历所有中间岛屿（不重复）之后到达终点所需要的最少的时间。

Sample Input

样例输入1：
4
0 10 20 999
5 0 90 30
99 50 0 10
999 1 2 0

样例输入2：
5
0 18 13 98 8
89 0 45 78 43 
22 38 0 96 12
68 19 29 0 52
95 83 21 24 0

Sample Output

样例输出1：
100

样例输出2：
137

Hint

提示： 
对于样例输入1：路飞选择从起点岛屿1出发，依次经过岛屿3，岛屿2，最后到达终点岛屿4。花费时间为20+50+30=100。 
对于样例输入2：可能的路径及总时间为： 
1,2,3,4,5: 18+45+96+52=211 
1,2,4,3,5: 18+78+29+12=137 
1,3,2,4,5: 13+38+78+52=181 
1,3,4,2,5: 13+96+19+43=171 
1,4,2,3,5: 98+19+45+12=174 
1,4,3,2,5: 98+29+38+43=208 
所以最短的时间花费为137 
单纯的枚举在N=16时需要14!次运算，一定会超时。

 

 

 

 

-----------------------------------------------------我是分割线^_^---------------------------------------------------------------- 

 

 

 

 

终于来了一题熟悉的题材了，海贼王呀，看了多少年了，真是令人振奋，这次题目的新姿势也是挺好的记录素材，一开始

我以为是求最短路，就三下五除二用五行代码想去解决它，结果发现原来还要遍历全部的岛屿，不愧是要成为海贼王的男人

目标就是宏大，倒是给我找了不少麻烦，用递归采用深度优先的方法写出来以后忍不住交了一发，结果当然超时了，因为

题目有提示嘛，直接遍历会有14！种情况，不超时才怪，后来去网上搜了一下改进方法，长姿势了，原来路径还可以使用

二进制进行标记，厉害，哈哈哈哈哈

 

说一说标记方法，就是下面打开的state数组，一维表示目前的所在的岛屿，二维表示表示到达该岛屿时的路径情况，

比如二维开了1<<5,就是100000，下面的递归第三个参数便是记录这个的，一开始是在第一个岛，land_state就是1，

从第一个岛到了第二个岛就让state_land+(1<<2)(注意优先级),然后state_land就变成了101，如果在这个基础上继续从第二到第三个岛，

就继续加，state_land+(1<<3),变成了1101，意思很清楚了，101表示走过了1->2,而1101表示走过了1->2->3,对，就是这个

意思啦！

 

 

#include<cstring>
#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;

#define INF 0x3f3f3f3f
int maze[20][20];
int state[25][1<<20];
bool vis[20];
int n;
int ans;

void DFS(int cur_land, int time, int total_land, int land_state) {
    if (time >= ans) return ;
    if (state[cur_land][land_state] == -1 || state[cur_land][land_state] > time) {/*state数组初始化为-1，
如果这种状态为-1表示没有出现过，记录下来，如果出现过，比较与之前出现过的大小如果比之前出现过的还大，
那这种状态肯定不是最好的，返回，如果现在这个状态比之前那个状态花的时间少就更新最优解，理解了吧*/
        state[cur_land][land_state] = time;
    } else{        return ;
    }
    if (cur_land == n && total_land == n) {
        ans = min(ans, time);
        return ;
    }
    for (int i = 2; i <= n; i++) {
        if (vis[i]) continue;
        vis[i] = 1;
        DFS(i, time + maze[cur_land][i], total_land + 1, land_state + (1<<i));//就是上面说的那样啦
        vis[i] = 0;
    }
}

int main()
{
    //freopen("input.txt", "r", stdin);

    while (cin>>n) {
        memset(maze, 0, sizeof(maze));
        memset(vis, 0, sizeof(vis));
        memset(state, -1, sizeof(state));
        ans = 0x3f3f3f3f;
        for (int i = 1; i <= n; i++) {
            for (int j = 1;j <= n; j++) {
                cin>>maze[i][j];
            }
        }
        DFS(1, 0, 1, 1);
        cout<<ans<<endl;
    }
    return 0;
}