P1439 【模板】最长公共子序列

许久没有刷题，认为一个小学生教练到了普及一等的水平就可以安稳的睡了。孩子们外出上学的梦想湮灭。想传出去的球又回来了，孩子水平高了很多，我安心的看着他们进步。弊端逐渐显露，没有人带领，他们总是陷入各种迷茫。这种带领不一定是知识上的，也许就是精神上的，那么我也重新打开两年前的刷题暂停键，陪伴他们一起前行。

这道题非常神奇。对于一个有着简单背包、线性动态规划基础的中年人来说非常的虐。

首先，我是这样写的。

#include<iostream>
#include<cstdio>
using namespace std;
int a[100000],b[100000];
int f[10000][10000];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&b[i]);
    }
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    {
        
        if(a[i]==b[j])
        {
            f[i][j]=max(f[i][j],f[i-1][j-1]+1);
        }
        else
        {
            f[i][j]=max(f[i-1][j],f[i][j-1]);
        }
    }
    cout<<f[n][n];
    return 0;
}

规规整整的最长公共子序列动态规划（也苦苦啃了半天）

提交 50分

这才关注数据范围，10^5 ，n^2一定崩。

于是发奋看题解，了解到离散的方式来处理。

于是有了这样的变形，感觉比n^2高效了一些。能看懂这个离散，把公共子序列变为LIS 最长不下降子序列，是看了阮行止大佬的一篇题解

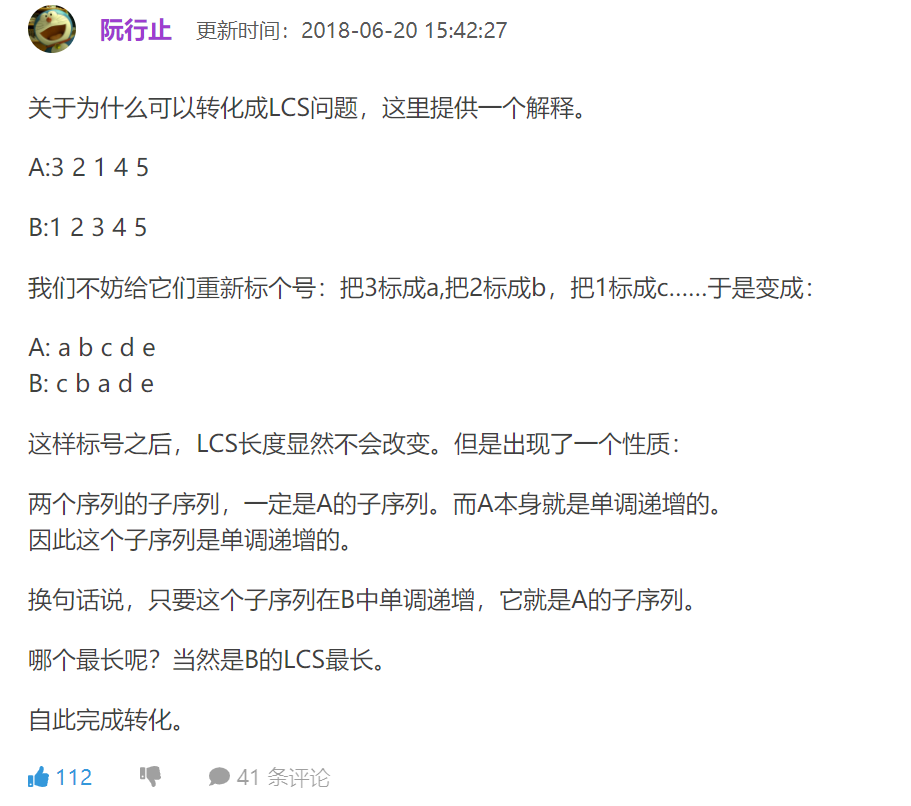
大佬一语点破梦中人，为了让自己更清晰，我直接把第二个b数组弄成了一个相对于 a位置信息的数组，这样只要求b的lis问题就可以了。

#include<iostream>
#include<cstdio>
using namespace std;
int a[100000],b[100000],map[100000],t,f[100000],ans;
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        map[a[i]]=i;
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&t);
        b[i]=map[t];
    }
    for(int i=1;i<=n;i++)
    {
        f[i]=1;
        for(int j=1;j<=i-1;j++)
        if(b[i]>b[j])
        {
            f[i]=max(f[i],f[j]+1);
        }
    }
    for(int i=1;i<=n;i++)
    {
        ans=max(f[i],ans);
    }
    cout<<ans;
}

结果还是50分。虽然提高了效率，但是还是n^2

导弹拦截只得了一半分的锅又出来了，当时懒得去理解nlogn的算法，总要还。开始看这方面资料LIS nlogn算法

大佬谆谆教诲的 传送门  

有认识一个新的盲区，关于lowerbound和upperbound，再一次百度  另外一个大佬谆谆教诲的 传送门

看懂了，AC。未来顺便补上导弹拦截的空缺。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int a[100000],b[100000],map[100000],t,f[100000],ans,temp[100000];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        map[a[i]]=i;
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&t);
        b[i]=map[t];
    }
    int len=0;
    for(int i=1;i<=n;i++)
    {
        if(b[i]>temp[len])
        {
            temp[++len]=b[i];
            continue;
        }
        t=upper_bound(temp,temp+len+1,b[i])-temp;
        temp[t]=b[i];
    }
cout<<len<<endl;
}